力的平移定理：同一刚体上任一点O

第2、3 章已经研究了平面汇交力系与平面力偶系的合成与平衡问题。为了将平面一般力系简化为这两种力系,首先必须解决力的作用线如何平行移动的问题。

设刚体的A 点作用着一个力F,在此刚体上任取一点O(图4.3)。如何才能把力F 平移到O 点,而不改变其原来的作用效应? 为此,可在O 点加上两个大小相等、方向相反,与F 平行的力F′和F″,且F′=F″=F。根据加减平衡力系公理,F、F′和F″与图示的F 对刚体的作用效应相同。显然,F″和F 组成一个力偶,其力偶矩为:

图4.3

这3 个力可转换为作用在O 点的一个力和一个力偶。由此可得力的平移定理:作用在刚体上的力F,可以平移到同一刚体上的任一点O,但必须附加一个力偶,其力偶矩等于原力F 对新作用点O 之矩。(www.xing528.com)

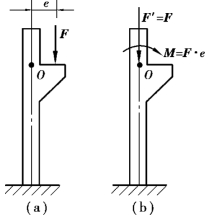
图4.4

顺便指出,根据上述力的平移的逆过程,还可将共面的一个力和一个力偶合成为一个力。该力的大小和方向与原力相同,其作用线间的垂直距离为:

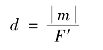
力的平移定理是一般力系向一点简化的理论依据,也是分析力对物体作用效应的一个重要方法。例如,如图4.4(a)所示的厂房柱,受到吊车梁传来的荷载F 的作用,为分析F 的作用效应,可将力F 平移到柱的轴线上的O 点上,根据力的平移定理得一个力F′,同时还必须附加一个力偶。力F 经平移后,它对柱子的变形效果就可以很明显地看出,力F′使柱子轴向受压,力偶使柱弯曲。