平面力偶系的平衡条件

平面力偶系可以合成为一个合力偶。当合力偶矩等于零时,则力偶系中的各力偶对物体的转动效应相互抵消,物体处于平衡状态。因此,平面力偶系平衡的必要和充分条件是:力偶系中所有各力偶矩的代数和等于零。用式子表示为:

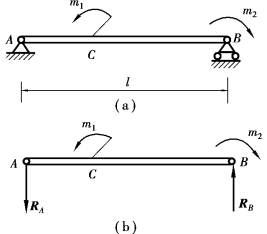
图3.12

【例3.5】　在梁AB 上作用两个力偶,其力偶矩的大小分别为m1 =120 kN·m,m2 =360 kN·m,转向如图3.12(a)所示。梁跨度l =6 m,重量不计。求A、B 处的支座反力。

【解】　取梁AB 为研究对象,作用在梁上的力有:两个已知力偶m1、m2 和支座A、B 的反力RA、RB。如图3.12(b)所示,B 处为可动铰支座,其反力RB 的方位铅垂,指向假定向上。A 处为固定铰支座,其反力RA 的方向本属未能确定的,但因梁上只受力偶作用,故RA 必须与RB 组成一个力偶才能与梁上的力偶平衡,所以RA 的方向也为铅垂,指向假定向下。由式(3.5)得:

故(www.xing528.com)

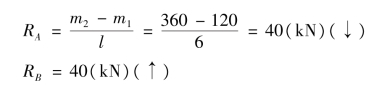
求得的结果为正值,说明原假设RA 和RB 的指向就是力的实际指向。

【例3.6】　丁字横梁由固定铰A 及链杆CD 支持,如图3.13(a)所示。在AB 杆的B 端有一个力偶作用,其力偶矩m=100 N·m,转向如图3.13 所示。若各杆自重不计,试求A、D 处的约束反力。

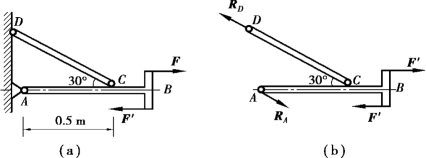
图3.13

【解】　取整个构架为研究对象。链杆CD 是二力杆,故支座D 的约束反力RD 沿CD 杆中心线。另外,根据力偶只能与力偶平衡的性质,支座A 的约束反力RA 与RD 也必须组成一个力偶与已知力偶相平衡,故RA 与RD 等值且反向平行,如图3.13(b)所示。由平面力偶系的平衡条件得: