合力矩定理是什么？原理、公式及应用详解

平面汇交力系对物体的作用效应可以用它的合力R 来代替。这里的作用效应包括物体绕某点转动的效应,而力使物体绕某点的转动效应由力对该点之矩来度量。因此,平面汇交力系的合力对平面内任一点之矩等于该力系中的各分力对同一点之矩的代数和。用公式可表示为:

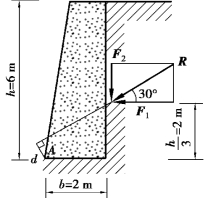
图3.3

合力矩定理是力学中应用十分广泛的一个重要定理。详细证明留待第4 章完成。

【例3.2】　图3.3 所示每1 m 长挡土墙所受土压力的合力为R,其大小R=200 kN,求土压力R 使墙倾覆的力矩。

【解】　挡土墙与土的连接并不牢固,所以土压力R 可使挡土墙绕A 点倾覆,求R 使墙倾覆的力矩,就是求它对A 点逆时针的力矩。由于R 的力臂求解较麻烦,但如果将R 分解为两个分力F1 和F2,而两分力的力臂是已知的。因此,根据合力矩定理,合力R 对A 点之矩等于F1、F2 对A 点之矩的代数和。

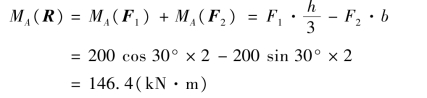
【例3.3】　求图3.4 所示各分布荷载对A 点的矩。

【解】　沿直线平行分布的线荷载可以合成为一个合力。合力的方向与分布荷载的方向相同,合力作用线通过荷载图的重心,其合力的大小等于荷载图的面积。(www.xing528.com)

根据合力矩定理可知,分布荷载对某点之矩就等于其合力对该点之矩。

①计算图3.4(a)所示三角形分布荷载对A 点的力矩。

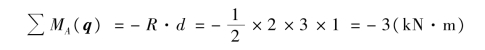
②计算图3.4(b)所示均布荷载对A 点的力矩。

③计算图3.4(c)所示梯形分布荷载对A 点的力矩。此时,为避免求梯形形心,可将梯形分布荷载分解为均布荷载和三角形分布荷载,其合力分别为R1 和R2,则有:

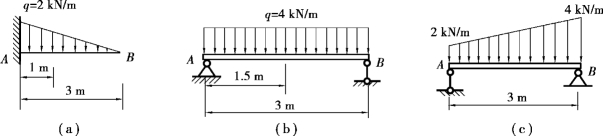
图3.4