解析条件：平面汇交力系的平衡

由式(2.8)可知,合力的大小为:

上式中(∑X)2 和(∑Y)2 恒为正值,所以,要使R = 0,∑X 和∑Y 就必须同时等于零。

因此,平面汇交力系平衡的必要与充分的解析条件是:力系中各分力在任意两个坐标轴上投影的代数和分别等于零。式(2.9)称为平面汇交力系的平衡方程。它们相互独立,应用这两个独立的平衡方程可求解两个未知量。

解题时,未知力指向有时可以预先假设。若计算结果为正值,表示假设力的指向就是实际的指向;若计算结果为负,表示假设力的指向与实际指向相反。在计算中,适当地选取投影轴,可使计算简化。

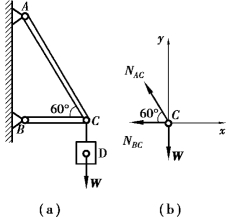
图2.11

下面举例说明平面汇交力系平衡条件的应用。

【例2.4】　求图2.11(a)所示三角支架中杆AC 和杆BC所受的力。(已知重物D 重W=10 kN)

【解】　①取铰C 为研究对象。因杆AC 和杆BC 都是二力杆,所以NAC 和NBC 的作用线都沿杆轴方向。现假定NAC、NBC均为拉力,画受力图如图2.11(b)所示。

②选取坐标系如图2.11(b)所示。

③列平衡方程,求解未知力NAC和NBC。

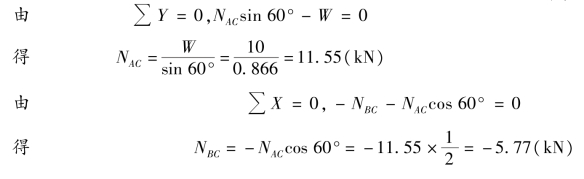
因求出的结果NBC为负,说明假定的指向与实际指向相反,即杆AC 受拉,杆BC 受压。

【例2.5】　如图2.12(a)表示起吊构件的情形,构件W=18 kN,钢丝绳与水平线的夹角为45°。求构件匀速上升时,钢绳的拉力是多少?

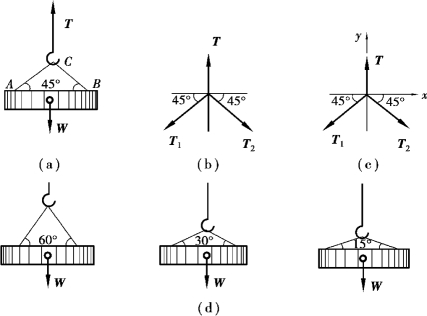
图2.12

【解】　整个体系在重力W 和绳的拉力T 作用下平衡,是二力平衡问题,于是得T =W =18 kN。

①取吊钩C 为研究对象。设绳CA 的拉力T1,绳CB 的拉力T2,画受力图[图2.12(b)]。

②选取坐标系如图2.12(c)所示。(www.xing528.com)

③列平衡方程,求解未知力T1 和T2:

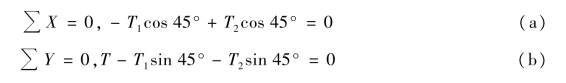
由式(a)得T1 =T2,代入式(b):

得

图2.12(d)绘出了当α 角分别为60°、30°、15°的情形。α 角越小,拉力T1 及T2 越大。在现场施工中,必须注意防止发生因吊索AC、BC 过短而被拉断的事故。

【例2.6】　简易起重机如图2.13 所示。B、C 为铰链支座。钢丝绳的一端缠绕在卷扬机D上,另一端绕过滑轮A 将重为W=20 kN 的重物匀速吊起。杆件AB、AC 及钢丝绳的自重不计,各处的摩擦不计。试用解析法求杆件AB、AC 所受的力。

【解】　①取滑轮A 为研究对象。杆件AB 及杆件AC 仅在其两端受力且处于平衡,因此都是二力杆,设都为受拉杆;由于不计摩擦,钢丝绳两端的拉力应相等,都等于物体的重量W。由于滑轮受绳子的合力通过轮心,故可以不考虑滑轮的尺寸,滑轮的受力图如图2.13(b)所示。

②求解。取坐标轴Axy 如图2.13(b)所示,利用平衡方程,得:

由于T1 =T2 =W=20 kN,代入上式即得:

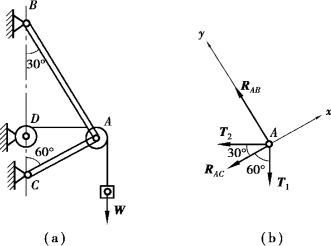
图2.13

RAC为负值,说明AC 杆实际受力方向与假设方向相反,AC 杆为受压力。

解得:

RAB为正值,说明AB 杆实际力方向与假设方向相同,AB 杆为受拉力。