平面力系合成解析法

几何法用来对物体进行受力分析,用来具体计算的是解析法。这种方法是以力在坐标轴上的投影为基础进行计算的。

1)力在平面直角坐标轴上的投影

如图2.4 所示,设力F 用矢量AB 表示,取直角坐标系Oxy,使力F 在Oxy 平面内。过力矢的两端点A 和B 分别向x、y 轴作垂线,得垂足a、b 及a′、b′,则线段ab 与a′b′的长度加以正负号分别称为力F 在x、y 轴上的投影,记作X、Y。并规定:当力的始端的投影到终端的投影的方向与投影轴的正向一致时,力的投影取正值;反之,当力的始端的投影到终端的投影的方向与投影轴的正向相反时,力的投影取负值。

设力F 与x 轴的夹角为α,则从图2.4 可知:

一般情况下,若已知力F 与x 和y 轴所夹的锐角分别为α、β,则该力在x、y 轴上的投影分别为:

即力在坐标轴上的投影,等于力的大小与力和该轴所夹锐角余弦的乘积。当力与轴垂直时,力在该轴上的投影为零;力与轴平行时,力在该轴上的投影大小的绝对值等于该力的大小。

反过来,若已知力F 在坐标轴上的投影X、Y,也可求出该力的大小和方向:

式中　α——力F 与x 轴所夹的锐角,其所在的象限由X、Y 的正负号来确定。

在图2.4 中,若将力沿x、y 轴进行分解,可得分力Fx 和Fy。应当注意,力的投影和分力是两个不同的概念:力的投影是标量,它只有大小和正负;而力的分力是矢量,有大小和方向。从图2.4 可见,在直角坐标系中,分力的大小和力在对应坐标轴上投影的绝对值是相同的。

力在平面直角坐标轴上的投影计算,在力学计算中应用非常普遍,必须熟练掌握。

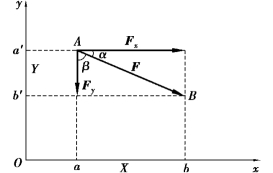
图2.4

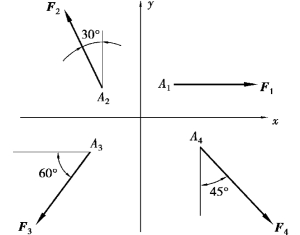
图2.5

【例2.1】　如图2.5 所示,已知F1 =100 N,F2 =200 N,F3 =300 N,F4 =400 N,各力的方向如图所示,试分别求各力在x 轴和y 轴上的投影。

【解】　根据式(2.5),得:

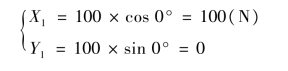
2)合力投影定理

如图2.6 所示,设有一平面汇交力系F1、F2、F3 作用在物体的O 点[图2.6(a)]。从任一点A 作力多边形ABCD,如图2.6(b)所示。则矢量AB 就表示该力系的合力R 的大小和方向。如图2.6(b)所示,取任一轴x,把各力都投影在x 轴上,并且令X1、X2、X3 和Rx 分别表示各分力F1、F2、F3 和合力R 在x 轴上的投影,由图2.6(b)可得:

而

因此可得:

这一关系可推广到任意个汇交力的情形,即:

(www.xing528.com)

由此可见,合力在任一轴上的投影,等于力系中各分力在同一轴上投影的代数和。这就是合力投影定理。

图2.6

图2.7

3)用解析法求平面汇交力系的合力

如图2.7 所示,当平面汇交力系为已知时,可选直角坐标系,先求出力系中各力在x 轴和y轴上的投影,再根据合力投影定理求得合力R 在x、y 轴上的投影Rx、Ry。从图2.7 中的几何关系,合力R 的大小和方向由下式确定:

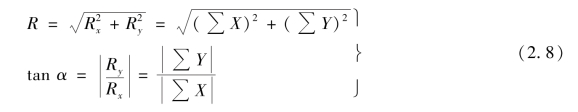
式中　α——合力R 与x 轴所夹角的锐角;

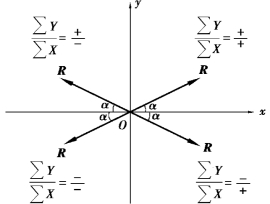
图2.8

R——在哪个象限由∑X 和∑Y 的正负号来确定,如图2.8 所示。合力的作用线通过力系的汇交点O。

【例2.2】　如图2.9(a)所示,固定的圆环上作用着共面的3 个力,已知F1 =10 kN,F2 =20 kN,F3 =25 kN,三力均通过圆心O。试分别用几何法和解析法求此力系合力的大小和方向。

【解】　运用两种方法求解合力。

①几何法。取比例尺为:1 cm 代表10 kN,画力多边形,如图2.10(b)所示,其中从起点a 向终点d 作矢量ad,即得合力R。由图上量得,ad =4.4 cm,根据比例尺可得,R=44 kN;合力R 与水平线之间的夹角用量角器量得α=22°。

图2.9

②解析法。取如图2.9(a)所示的直角坐标系Oxy,则合力的投影分别为:

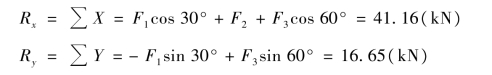
则合力R 的大小为:

合力R 的方向为:

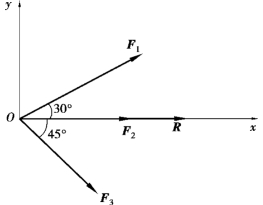
图2.10

由于Rx >0,Ry >0,故α 在第一象限,而合力R 的作用线通过汇交力系的汇交点O。

【例2.3】　如图2.10(a)所示,一平面汇交力系作用于O 点。已知F1 =200 N,F2 =300 N,F3 方向如图2.10所示。若此力系的合力R 与F2 沿同一直线,用解析法求F3 与合力R 的大小。

【解】　取如图2.10 所示的坐标系。由题可知R 沿x 轴正向,则: