圆柱螺旋扭转弹簧的设计及应用

扭转弹簧常用于压紧、储能或传递扭矩。它的两端带有杆臂或挂钩，以便固着或加载。扭转弹簧的主要几何尺寸和特性曲线如图14.8 所示。扭转弹簧所受的外力为转矩T扭，所产生的变形为扭转角φ。扭转弹簧的工作应力也要在其材料的弹性极限范围内才能正常工作，载荷T 与扭转角φ 的关系如图14.8 所示。至于最小转矩和最大转矩、最大转矩与极限转矩间的关系可参考压缩弹簧中给出的数值。

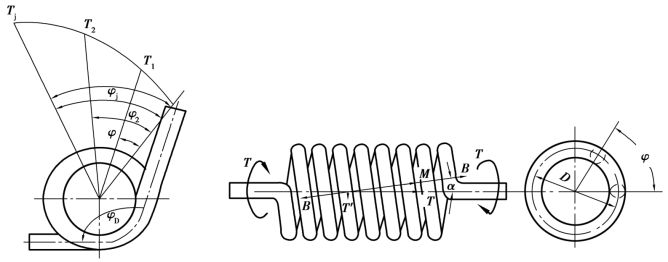
图14.8　扭转弹簧及其特性曲线

在自由状态下，扭转弹簧的各圈间应留有少量间隙（δ≈0.5 mm）；否则，在弹簧正常工作时，弹簧各圈间将彼此接触并产生摩擦和磨损。如图14.9 所示为用冷卷制作的扭转弹簧的4 种端部结构形式。其中，图14.9（d）直臂扭转NⅤ为推荐使用。

若在垂直于弹簧轴线平面内受一转矩T 作用的扭转弹簧，在其弹簧丝的任一截面上将作用有弯矩M=Tcosα 和转矩T扭=Tsinα（见图14.7）。由于螺旋角很小，故转矩T 可忽略不计，并可认为M≈T扭。因此，扭转弹簧的弹簧丝中主要受弯矩M 的作用。

图14.9　扭转弹簧端部结构

由上述分析可知，扭转弹簧应按受弯矩的曲梁来计算，在它的任一截面上的应力分布情况与压缩弹簧完全相似。只是应力为弯曲应力，其最大弯曲应力σmax（单位为MPa）及强度条件（以Tmax代T，N·mm）为

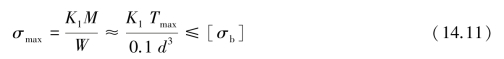
式中　W——弯曲时的截面系数。圆弹簧丝，方弹簧丝；

　　　K——扭转弹簧的曲度系数。圆弹簧丝，方弹簧丝；(www.xing528.com)

　　　[σb]——许用弯曲应力，取 [σb]=1.25[]。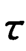

扭转弹簧因扭转变形而产生的扭转角φ（°）可按材料力学中的公式作近似计算，即

式中　I——弹簧丝截面的轴惯性矩，mm4，对于圆形截面，I=；

　　　E——弹簧材料的弹性模量，MPa，见表14.2。

可得出计算扭转弹簧圈数的计算公式为

扭转弹簧的弹簧丝长度为

式中　Lh——制作挂钩或杆臂的弹簧丝长度。