圆柱螺旋压缩弹簧设计与应用

如图14.4 所示，弹簧节距为p，自由状态下弹簧长度H0，各圈之间有一定的间距。弹簧两端各有0.75～1.25 圈与弹簧座相接触的支承圈，俗称死圈，死圈不参与弹簧变形，其端面应与弹簧轴线垂直。

弹簧在工作前，通常受预压缩力Fmin，以使其可靠地固定在安装位置上。力Fmin称为弹簧的最小载荷。在最小载荷Fmin作用下，弹簧的长度为H1，弹簧的压缩量为λmin。当弹簧达到最大工作载荷Fmax时，弹簧压缩量增至λmax，弹簧长度从H1 减至H2，λmax与λmin之差即为弹簧的工作行程h。Flim是弹簧的极限载荷，即在Flim作用下弹簧丝内的应力达到了弹簧材料的屈服极限，这时相应的弹簧长度为H3，压缩量为λlim。

弹簧的最小载荷通常取Fmin=（0.1～0.5）Fmax。实际应用过程中，一般不希望弹簧失去其线性特性，故最大载荷小于极限载荷，通常满足Fmax≤0.8 Flim。

（1）强度计算

现在对如图14.5 所示圆形截面弹簧丝的压缩弹簧承受轴向载荷F 的情况进行分析。

图14.4　圆柱螺旋压墙弹簧的特性曲线

由图14.5（a）可知，由于弹簧丝具有升角α，故通过弹簧轴线的截面上，弹簧丝的截面A—A 呈椭圆形，该截面上作用着力F 及扭矩T=FD/2。因此，在弹簧丝的法向截面B—B 上则作用有横向力F cos α、轴向力F sin α、弯矩M=T sin α 及扭矩T′=T cos α。

弹簧中径D 与簧丝直径d 之比，称为旋绕比C（又称弹簧指数），即C=D/d。当其他条件相同时，C 值越小，弹簧丝内、外侧的应力差越悬殊，材料利用率越低；反之，C 值过大，应力过小，弹簧卷制后将有显著回弹，加工误差大。因此，通常C=4 ～14，不同簧丝直径推荐用旋绕比参照表14.6 选用。

根据理论推导，在轴向压力F 作用下，压缩弹簧的最大切应力可按式（14.2）计算。

由于弹簧的螺旋升角一般取为α=5°～9°，故sin α≈0；cos α≈1（见图14.5（b）），则截面B—B 上的应力（见图14.5（c））可近似地取为

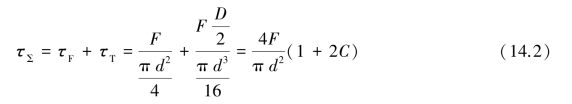
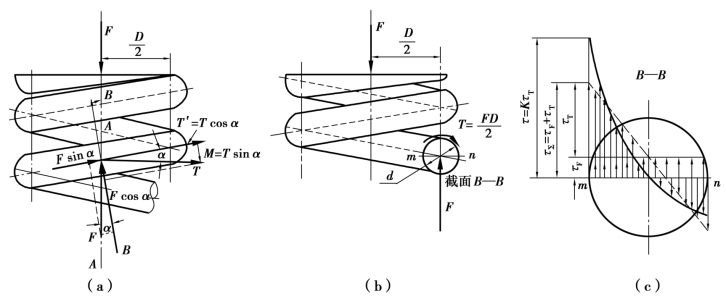
图14.5　圆柱螺旋压缩弹簧的受力及应力分析

表14.6　常用旋绕比C 值

弹簧丝内侧的最大应力及强度条件可表示为

式中，弹簧曲度系数K 对于圆截面弹簧丝可计算为

(www.xing528.com)

在求圆弹簧丝直径d 时，应以Fmax替F，并以D=Cd 代入式（14.3），得到

式中，许用切应力[]可根据弹簧材料和工作特点选取。

在用式（14.3）计算时，因旋绕比C 和许用切应力[]均与簧丝直径d 有关。常用试算的方法，求弹簧丝的直径。

（2）刚度计算

设计弹簧时，强度计算的目的在于确定弹簧中径D 和簧丝直径d，而刚度计算的目的在于确定弹簧的圈数。

当压缩弹簧承受轴向压力时，在圆形簧丝截面上作用有转矩T，从而产生扭转变形（见图14.5）。经积分推导，得到圆形弹簧丝螺旋弹簧承受载荷F 后所产生的变形量

式中　n——弹簧的有效工作圈数；

　　　G——弹簧材料的切变模量，MPa，见表14.2。

利用式（14.6），可求出所需的弹簧有效圈数为

使弹簧产生单位变形所需的载荷kF，称为弹簧刚度，即

弹簧刚度是表征弹簧性能的主要参数之一。它表示使弹簧产生单位变形时所需的力，刚度越大，需要的力越大，则弹簧的弹力就越大。但影响弹簧刚度的因素很多，从式（14.8）可知，kF与C 的3 次方成反比，即C 值对kF的影响很大。因此，合理地选择C 值就能控制弹簧的弹力。另外，kF 还与G、d、n 有关。在调整弹簧刚度kF 时，应综合考虑这些因素的影响。

（3）稳定性计算

当压缩弹簧的圈数较多时，还应校验其稳定性指标，即高径比b=H0/D。在高径比b 值较大的情况下，当压力达到一定值时，弹簧会突然发生侧向弯曲的现象，使弹簧刚度突然降低，这种现象称为弹簧的失稳，这是弹簧正常工作所不允许的。

压缩弹簧的稳定性与弹簧两端的支承方式有关。为了保证弹簧不失稳，一般需要满足以下条件：弹簧两端均为回转端时，b≤2.6；当弹簧一端同定、一端回转时，b≤3.7；当弹簧两端均同定时，b≤5.3。若b 不能满足要求，为了保证弹簧的稳定性，应在弹簧外侧加导向套或在弹簧内侧加导向杆。

（4）结构尺寸计算

压缩弹簧在最大载荷下应留有少量间隙δ，以免各圈彼此接触，通常取δ≥0.1d。压缩弹簧的结构尺寸计算可参考相关资料。