轴的强度校核计算方法

进行轴的强度计算时，应根据轴的受载及应力的具体情况，采取相应的计算方法，选取相应的许用应力、对于仅（或主要）承受转矩的轴（传动轴），应按扭转强度条件计算；对于仅承受弯矩的轴（心轴），应按弯曲强度条件计算；对于既承受弯矩又承受转矩的轴（转轴），应按弯扭合成强度条件计算，必要时还应按疲劳强度条件进行精确校核。下面介绍几种常用的计算方法。

（1）按扭转强度计算

扭转强度法是只按轴所受的转矩来计算轴的强度，主要适用于传动轴或不太重要的轴的强度计算。在进行轴的结构设计时，也常用于估算轴的最小直径。

对于传递转矩的圆截面实心轴，其扭转强度条件为

式中　——转矩T（N·mm）在轴上产生的扭剪应力，MPa；

　　　[]——材料的许用剪切应力，MPa；

　　　P——轴所传递的功率，kW；

　　　WT——抗扭截面系数，mm3，对圆截轴；

　　　N——轴的转速，r/min；

　　　D——轴的直径，mm。

上式可用作传动轴强度计算，也可用于初步估算转轴最细部分直径，但必须把轴的许用扭剪应力[]适当降低，其值查表10.2，以补偿弯矩对轴强度的影响。将降低后的许用应力代入上式，可得轴设计公式为

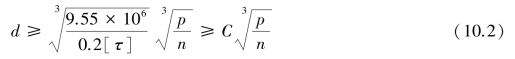
式中　C——由轴的材料和承载情况确定的常数，见表10.2。

表10.2　常用材料的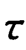［］值和C 值

注：当作用在轴上的弯矩比传递的转矩小或只传递转矩时，C 取较小值；否则，取较大值。

按式（10.2）计算得到的直径，一般作为轴的最小直径。如果在该处有键槽，则应考虑它对轴的削弱程度。一般，有一个键槽直径增加5%，两个键槽直径增大10%，最后需要将轴径圆整为标准值。

（2）按弯扭合成进行强度计算

轴的结构设计完成后，根据轴的几何尺寸和形状就完全可确定轴上载荷的大小、方向及作用点和轴的支点位置，从而可求出支反力及弯矩。此时，可按弯扭合成强度条件进行计算。一般的轴用这种方法计算即可。具体的计算步骤如下：

1）作出轴的计算简图（即建立力学模型）

即画出轴的受力计算简图，标出各作用力的大小、方向和作用点的位置。画简图时，应注意以下问题：进行强度计算时，通常把轴视作一简支梁，轴上支反力的作用点由轴承的类型和布置方式有关，可按图10.24 来确定。其中，图10.24（b）中的a 值可通过查滚动轴承样本或手册来确定。而图10.24（d）中的e 值与滑动轴承的宽度B 和内径d 有关。当B≤d 时，e=0.5B；当B>d 时，e=0.5d，但不应小于（0.25 ～0.35）B；对于调心轴承，取e=0.5l。作用在轴上零件的载荷，一般按集中载荷考虑，其作用点取为零件轮缘宽度的中点，如图10.24（e）所示。作用于轴上的转矩，也可简化为从传动零件（如联轴器）轮毂宽度中点算起的转矩。

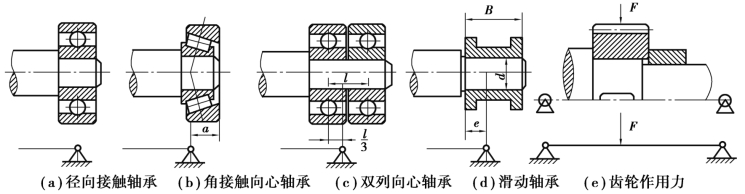
图10.24　轴的支反力作用点和受力简化

在作计算简图时，应先求出轴上受力零件的载荷（若为空间力系，应把空间力分解为圆周力、径向力和轴向力，然后把它们全部转化到轴上），并将其分解为水平分力和垂直分力，如图10.25（a）所示。然后求出各支承处的水平反力FNH。和垂直反力FNV（轴向反力可表示在适当的面上，图10.25（c）是表示在垂直面上，故标以）。

2）计算弯矩、作弯矩图

按上述受力计算简图，分别按水平面和垂直面计算各力产生的弯矩，按计算结果绘出水平面弯矩MH 图（见图10.25（b））和垂直面弯矩MV 图（见图10.25（c））。

图10.25　轴的载荷分析图

3）作合成弯矩图

计算出合成弯矩，绘出合成弯矩图（见图10.25（d））。

4）作转矩图

计算转矩（T），并画出转矩图，如图10.25（e）所示。

5）计算当量弯矩，确定危险截面

计算出轴所受的转矩和弯矩后，即可对轴的危险截面（指发生破坏可能性最大的截面，计算当量弯矩。

6）按弯扭组合强度校核

对某些危险截面作弯扭合成强度校核计算。对于钢制轴，可按第三强度理论计算，强度条件为

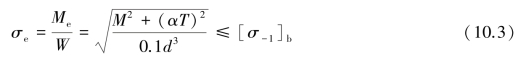(www.xing528.com)

由上式可推得轴设计公式为

式中　σe——当量应力，N/mm2；

　　　Me——当量弯矩，N·mm；

　　　W——轴计算截面的抗弯截面系数，mm2，计算公式见表10.3；

　　　α——由扭转剪应力性质而定的折算系，α=。

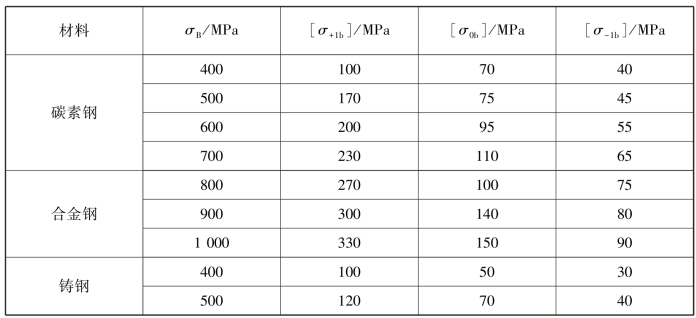
对于不变的转矩，取α≈0.3；对于脉动循环的转矩，取α≈0.6；对于对称循环的转矩，取α=1。如果单向回转的转矩，其变化规律不太清楚时，一般按照脉动变化的转矩处理。其中，[σ-1]b、[σ0]b、[σ+1]b 分别为对称循环、脉动循环及静应力状态下的许用弯曲应力，其值列于表10.4 中。

表10.3　抗弯、抗扭截面系数计算公式

表10.4　轴的许用弯曲应力

对于有键槽的截面，应将计算出的轴径加大5%左右。若计算出的轴径大于结构设计初步估算的轴径，则表明结构图中轴的强度不够，必须修改结构设计；若计算出的轴径小于结构设计的估算轴径，且相差不很大，一般就以结构设计的轴径为准。

对于一般工作条件下的转轴，按上述方法计算已足够精确。对于重载、尺寸受限制和重要的转轴，应采用更为精确的疲劳强度安全系数校核，其计算方法可查阅有关参考书。

（3）按疲劳强度安全系数校核

这种校核计算的实质在于确定变应力情况下轴的安全程度。在已知轴的外形、尺寸及载荷的基础上，即可通过分析确定出一个或几个危险截面（这时，不仅要考虑弯曲应力和扭转切应力的大小，而且要考虑应力集中和绝对尺寸等因素影响的程度），求出计算安全系数S，并应使其稍大于或至少等于设计安全系数S。采用安全系数法校核轴的疲劳强度时，其强度条件为

仅受法向应力时，应满足

仅受扭转切向应力时，应满足

以上诸式中的符号及有关数据已在第2章内说明，此处不再重复。设计安全系数值可按下述情况选取。

S=1.3～1.5，用于材料均匀，载荷与应力计算精确时。

S=1.5～1.8，用于材料不够均匀，计算精确度较低时。

S=1.8～2.5，用于材料均匀性及计算精确度很低，或轴的直径d>200 mm 时。

（4）按静强度条件进行校核

静强度校核的目的在于评定轴对塑性变形的抵抗能力。这对那些瞬时过载很大，或应力循环的不对称性较为严重的轴是很必要的。轴的静强度是根据轴上作用的最大瞬时载荷来校核的，静强度校核时的强度条件为

式中　——危险截面静强度的计算安全系数；

　　　——只考虑弯矩和轴向力时的安全系数，见式（10.9）；

　　　——只考虑扭矩时的安全系数，见式（10.10）；

　　　SS——按屈服强度的设计安全系数；SS=1.2～1.4，用于高塑性材料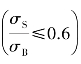制成的钢轴；SS=1.4～1.8，用于中等塑性材料制成的钢轴；SS=1.8 ～2，用于低塑性材料的钢轴；SS=2～3，用于铸造轴。

式中　——材料的抗弯和抗扭屈服极限，MPa，其中，=（0.55～0.62）σS；

　　　Mmax、Tmax——轴的危险截面上所受的最大弯矩和最大扭矩，N·mm；

　　　Famax——轴的危险截面上所受的最大轴向力，N；

　　　A——轴的危险截面的面积，mm2；

　　　W、WT——危险截面的抗弯和抗扭截面系数，mm3，见表10.5。