齿面接触疲劳强度计算优化

齿面点蚀是由于接触应力过大所引起的。齿轮的接触应力对小齿轮和大齿轮都是一样的，但随着啮合位置的变化，齿轮上载荷和综合曲率半径都在改变，导致接触应力发生变化。研究分析得知，在大、小齿轮均在单对齿啮合的最低点的接触应力最大，但考虑除接触应力以外其他因素的影响，点蚀首先出现的部位（大小齿轮单对齿啮合的最低点、节点或者期间），即该区域的齿面接触疲劳强度最弱。为此，应取单对齿啮合的最低点和节点处赫兹应力中应力较大者，分别作为大齿轮和小齿轮的齿面接触应力，但计算相当复杂，并且单对齿啮合的最低点与节点处的赫兹应力计算结果极为相近。为简化计算，同时保证一定的计算精度，以节点处的赫兹应力为代表进行齿面接触疲劳强度计算。齿轮啮合可看成分别以接触处曲率半径ρ1、ρ2 为半径的两个圆柱体的接触（由于弹性变形，接触区域实际为一窄平面），由于齿面点蚀一般发生在节线附近，因此，以节线处作为接触应力的计算部位。

如图8.19 所示为一对外啮合标准直齿圆柱齿轮在节点P 处的啮合，其最大接触应力可由赫兹应力公式计算，即

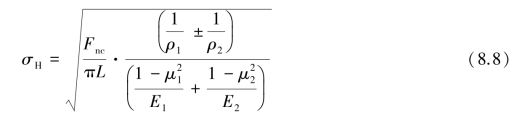
式中　Fnc——计算载荷，N，则

　　　L——轮齿接触线宽度，mm；

　　　ρ1、ρ2——两轮齿接触处的曲率半径。

图8.19　齿轮接触强度计算简图

对于标准直齿圆柱齿轮

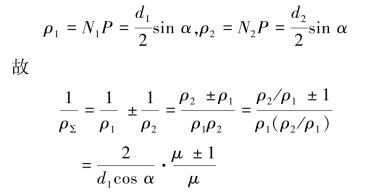
式中　ρΣ——节点处曲率的综合影响系数，“+”用于外啮合，“-”用于内啮合；

　　　u——齿数比，u=；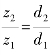

　　　μ1、μ2——两齿轮的泊松比；

　　　E1、E2——两齿轮的弹性模量。

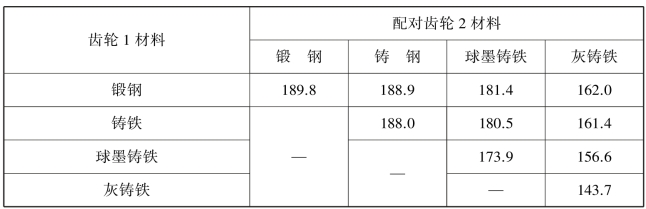
因泊松比和弹性模量都与齿轮材料有关，为简化计算，引入材料的弹性系数ZE（可查表8.5），令

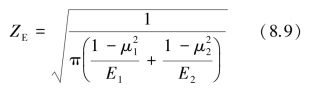(www.xing528.com)

表8.5　弹性系数ZE（MPa1/2）

直齿轮中合度1≤εα≤2，实际啮合时，并不总是单齿对啮合。因此，实际接触线长度由齿宽b 和端面重合度εα 决定。

实际接触线长度

式中　——接触疲劳强度计算的重合度系数。

将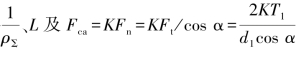代入赫兹应力计算表达式，得

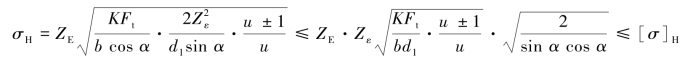
令（节点区域系数），则得接触疲劳强度条件为

引入齿宽系数ϕd=b/d1，则得

设计计算公式为

应用上述公式时，应注意以下3 点：

①一对齿轮啮合时，两齿面的接触应力相等，即σH=σH1=σH2，但它们的许用应力可能不相等，即[σH1]≠[σH2]。计算时，应将它们的较小值代入公式计算，才能保证大小齿轮在要求寿命内都不会出现点蚀。

②齿面接触疲劳强度与齿轮的直径或中心距的大小有关，即与m 和z 的乘积有关，而与模数的大小无关。当一对齿轮的材料及热处理、齿数比和齿宽系数一定的情况下，由齿面接触疲劳强度所决定的承载里仅与齿轮的中心距或分度直径有关。

③在一定载荷条件下，欲提高齿轮的齿面接触疲劳强度，主要可采用的措施有：改善齿轮材料和热处理方法以及加工精度，以便提高许用应力[σH] 加大中心距a、适当增加齿宽b、采用正传动变位增大啮合角，以便降低齿面接触疲劳应力。应注意轮齿过宽时，更容易产生偏载使齿向载荷分布更不均匀，从而达不到提高强度的目的。