齿轮传动的计算载荷优化方案

为了便于分析计算，通常取沿齿面接触线单位长度上所受的载荷进行计算。沿齿面接触线单位长度上的平均载荷p（N/mm）为

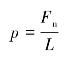
式中　Fn——作用于齿面接触线上的法向载荷，N；

　　　L——沿齿面的接触线长，mm。

法向载荷Fn 为公称载荷，在实际传动中，由于原动机及工作机性能的影响，以及齿轮的制造误差，特别是基节误差和齿形误差的影响，会使法向载荷增大。此外，在同时啮合的齿对间，载荷的分配并不是均匀的，即使在一对齿上，载荷也不可能沿接触线均匀分布。因此，在计算齿轮传动强度时，应按接触线单位长度上的最大载荷，即计算载荷pca（N/mm）进行计算，即

式中　K——载荷系数。

计算齿轮强度用的载荷系数K，包括使用系数KA、动载系数Kv 和齿间载荷分配系数Kα及齿向载荷分布系数Kβ，即

（1）使用系数KA

使用系数KA 是考虑齿轮啮合时外部因素引起的附加动载荷影响的系数。这种动载荷取决于原动机和工作机的特性、质量比、联轴器类型以及运行状态等。KA 的使用值应针对设计对象，通过实践确定。表8.3 所列使用系数KA 值可供参考。

表8.3　使用系数KA 值

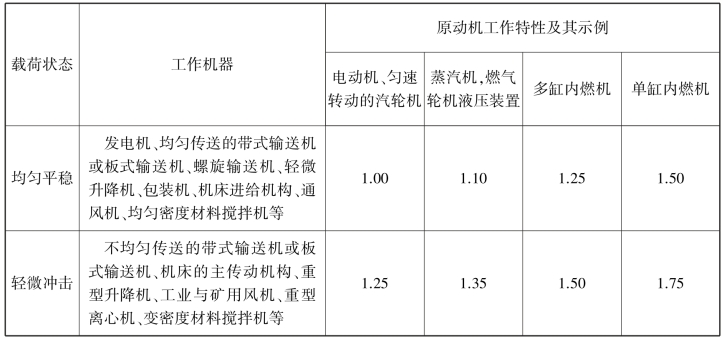
续表

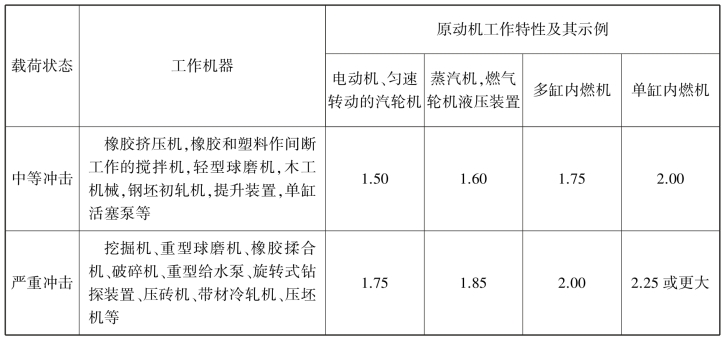
注：表中所列KA 值仅适用于减速传动；若为增速传动，KA 值约为表值的1.1 倍。当外部机械与齿轮装置间有挠性联接时，通常KA 值可适当减小。

（2）动载系数Kv

齿轮传动不可避免地会有制造及安装误差，轮齿受载后还要产生弹性变形。这些误差及变形实际上将使啮合轮齿的法向齿距pb1与pb2不相等（参看图例），因而轮齿就不能正确啮合传动，瞬时传动比就不是定值，从动齿轮在运转中就会产生角加速度，于是引起动载荷或冲击。对于直齿轮传动，轮齿在啮合过程中，不论是由双对齿啮合过渡到单对齿啮合，或是由单对齿啮合过渡到双对齿啮合的期间，啮合齿对的刚度变化也要引起动载荷。为了计及动载荷的影响，引入了动载系数Kv。

齿轮的制造精度及圆周速度对轮齿啮合过程中产生动载荷的大小影响很大。提高制造精度，减小齿轮直径以降低圆周速度，均可减小动载荷。

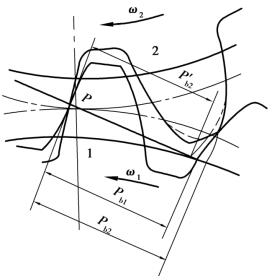
图8.10　从动轮齿修缘

为了减小动载荷，可将轮齿进行齿顶修缘，即把齿顶的小部分齿廓曲线（分度圆压力角α=20°的渐开线）修正成α>20°的渐开线。如图8.10 所示，因pb2>pb1，则后一对轮齿在未进入啮合区时就开始接触，从而产生动载荷。为此将从动轮2 进行齿顶修缘，图中从动轮2 的虚线齿廓即为修缘后的齿廓，实线齿廓则为未经修缘的齿廓。由图8.10 可明显地看出，修缘后的轮齿齿顶处的法节p′b2<pb1时，对修缘了的轮齿，在开始啮合阶段，相啮合的轮齿的法节差就小一些，啮合时产生的动载荷也就小一些。

如图8.11 所示的主动轮齿修缘，若pb1>pb2，则在后一对齿已进入啮合区时，其主动齿齿根与从动齿齿顶还未啮合。要待前一对齿离开正确啮合区一段距离以后，后一对齿才能开始啮合，在此期间，仍不免要产生动载荷。若将主动轮1 也进行齿顶修缘（见图8.11 主动轮齿修缘中虚线齿廓），即可减小这种载荷。

高速齿轮传动或齿面经硬化的齿轮，轮齿应进行修缘。但应注意，若修缘量过大，不仅重合度减小过多，而且动载荷也不一定就相应减小，故轮齿的修缘量应定得适当。

动载系数Kv 的实用值，应针对设计对象通过实践确定，或按有关资料确定。对于一般齿轮传动的动载系数Kv，可参考图8.12 选用。若为直齿圆锥齿轮传动，应按图中低一级的精度线及锥齿轮平均分度圆处的圆周速度vm 插取Kv 值。

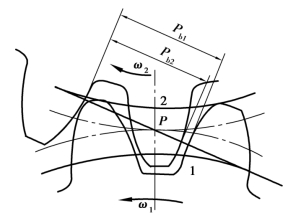
图8.11　主动轮齿修缘

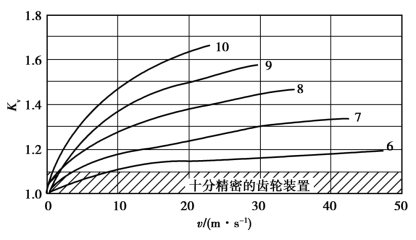
图8.12　动载系数Kv(www.xing528.com)

（3）齿间载荷分配系数Kα

一对相互啮合的斜齿（或直齿）圆柱齿轮，如在啮合区中有两对（或多对）齿同时工作时，则载荷应分配在这两对（或多对）齿上。

图8.13 中两对齿同时啮合的接触线总长L=PP′+QQ′。但由于齿距误差及弹性变形等原因，总载荷Fn 并不是按PP′/QQ′的比例分配在PP′及QQ′这两条接触线上。因此，其中一条接触线上的平均单位载荷可能会大于p，而另一条接触线上的平均单位载荷则小于p。进行强度计算时需按平均单位载荷大于p 的值计算。

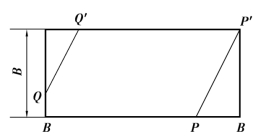
图8.13　啮合区齿间载荷的分配

为此，引入齿间载荷分配系数Kα。Kα 的值可用详尽的算法计算。对一般不需作精确计算的直齿轮和斜齿圆柱齿轮传动可查表8.4。

表8.4　齿间载荷分配系数KHα、KFα

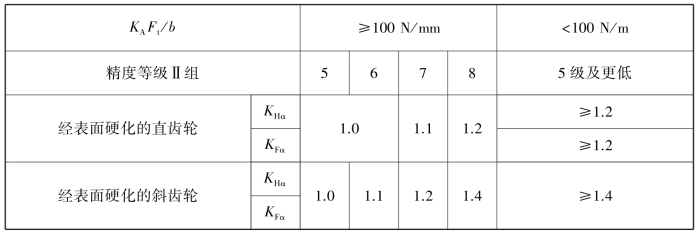
续表

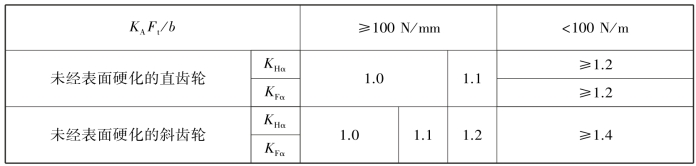
注：1.对修形齿轮，取KHα=KFα=1。
2.如大、小齿轮精度等级不同时，按精度等级较低者取值。
3.KHα为齿面接触疲劳强度计算用的齿间载荷分配系数，KFα为齿根弯曲疲劳强度计算用的齿间载荷分配系数。

（4）齿向载荷分布系数Kβ

如图8.14 所示，当轴承相对于齿轮作不对称配置时，受载前，轴无弯曲变形，轮齿啮合正常，两个节圆柱恰好相切；受载后，轴产生弯曲变形（见图8.15），轴上的齿轮也就随之偏斜，这就使作用在齿面的载荷沿接触线分布不均匀。

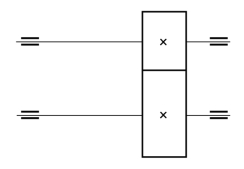
图8.14　轴承为不对称配置

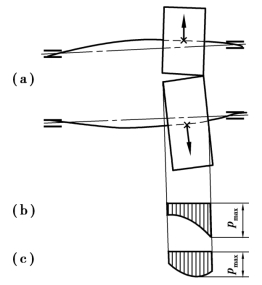
图8.15　轴受载弯曲变形后轮齿所受载荷

轴的扭转变形，轴承、支座的变形，以及制造、装配的误差等因素均会影响齿面上载荷不均匀分布。

计算轮齿强度时，考虑齿面上载荷沿接触线分布不均的现象，通常以齿向载荷不均匀系数Kβ 来表示齿面上分布不均的程度对轮齿强度的影响。

采用增大轴、轴承及支座的刚度，对称的配置轴承，以及适当的限制轮齿的宽度等措施。同时，应尽可能避免齿轮作悬臂布置（即两个支承皆在齿轮的一边），可有效地改善载荷沿接触线分布不均的程度。对高速、重载（如航空发动机）的齿轮传动应更加重视。

除此之外，也可把一个齿轮的轮齿做成鼓形（见图8.16）。当轴产生弯曲变形而导致齿轮偏斜时，鼓形齿齿面上载荷分布的状态对于载荷偏于轮齿一端的现象有所改善。

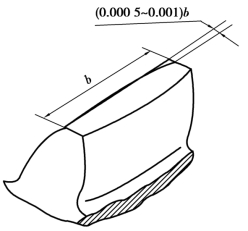
图8.16　鼓形齿

由于小齿轮轴的弯曲及扭转变形，改变了轮齿沿齿宽的正常啮合位置，因而相应于轴的这些变形量，沿小齿轮尺宽对轮齿作适当的修形，可大大地改善沿接触线分布不均的现象。这种沿尺宽对轮齿进行修形，多用于圆柱斜齿轮及人字齿轮传动，故称螺旋角修形。

对于一般的工业用齿轮，齿向载荷分布系数Kβ 可根据在轴上的支承情况、齿宽系数和齿面硬度从图8.17 中查取。图8.17 针对8 级精度齿轮，若为高于8 级精度的传动，Kβ 应降低5%～10%，但不小于1；若低于8 精度，Kβ 应增大5%～10%。

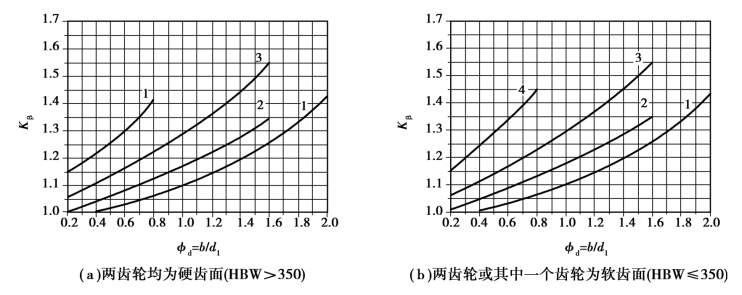
图8.17　齿向载荷分布系数Kβ

1—齿轮对称布置在两轴承中间；2—齿轮非对称布置在两轴承中间，且轴的刚度较大；3—齿轮非对称布置在两轴承中间，且轴的刚度较小；4—齿轮悬臂布置