机械零件强度计算

通用机械零件的强度分为静应力强度和变应力强度两个范畴。根据设计经验及材料的特性，通常认为在机械零件整个工作寿命期间应力变化次数小于103的通用零件，均可按静应力强度进行设计。利用材料力学中获得的知识，已可对零件进行一些基本的静应力强度设计。因此，本节对此不再加以讨论。要说明的一点是，在机械零件的设计实践中，按静强度设计计算之处还是很多的。即使是承受变应力的零件，在按疲劳强度进行设计的同时，还有不少情况需要根据受载过程中作用次数很少而数值很大的峰值载荷做静应力强度校核。本章以下主要讨论零件在变应力下的疲劳强度计算的问题。

按照强度准则设计机械零件时，根据材料性质及应力种类而采用的材料某个应力极限值，称为极限应力，以符号表示。对于脆性材料，在静应力作用下的主要失效形式是脆性破坏，故取材料的强度极限（）为极限应力。即；对于塑性材料，在静应力作用下的主要失效形式是塑性变形，故取材料的屈服极限（）为极限应力，即，而材料在变应力作用下的主要失效形式是疲劳破坏，故取材料的疲劳极限为极限应力，即=σr。

（1）材料的疲劳特性

在应力比为r 的循环应力作用下，应力循环N 次后，材料不发生疲劳破坏时的最大应力称为材料的疲劳极限，用表示。材料疲劳失效以前所经历的应力循环次数，称为疲劳寿命。不同应力比r 和不同疲劳寿命N 所对应的疲劳极限为σrN。疲劳强度设计中，就以零件的疲劳极限作为极限应力。

1）疲劳曲线（σ-N 曲线）：

疲劳曲线是指一定应力比r 下最大应力σmax与应力循环次数N 的关系曲线。

图2.3　材料疲劳曲线之一（σ-N 曲线）

图2.4　材料疲劳曲线之二（等寿命曲线）

由图2.3 可知，疲劳极限σrN随循环次数N 的增大而降低。但是，当N 超过某一次数（N0）时，曲线趋于水平，即疲劳极限σrN不再随N 的增大而减小，曲线与水平线交点的横坐标N0称为循环基数。通常以N0为界把曲线分为以下两个区段：

①无限寿命区当N≥N0 时，疲劳曲线为水平线，对应的疲劳极限为一定值，用σr 表示。它是表征材料疲劳强度的重要指标，是疲劳设计的基本依据。其中，最典型、最常用的是对称循环疲劳极限σ-1。在工程设计中，一般可认为，当材料受到的应力不超过σr 时，则可经受无限次应力循环而不破坏，故将σr 称为持久疲劳极限。

②有限寿命区为了区别于σr，把曲线上非水平段（N<N0 时）的疲劳极限σrN称为有限寿命疲劳极限。当材料受到的应力超过σr 时，在疲劳之前，只能经受有限次的应力循环。当N<103（104）时，疲劳极限接近或超过屈服点，不同循环次数N 下的疲劳极限几乎没有变化，此类疲劳称为低周疲劳。其特点是：应力水平高，疲劳寿命低。相对于低周疲劳，将N>103（104）时的疲劳，称为高周疲劳。

大多数钢的疲劳曲线形状类似图2.3。但是，高强度合金钢和有色金属的疲劳曲线没有水平线，不存在无限寿命区。因此，工程上常以某一循环次数（N0=108或5×108）下的有限寿命疲劳极限（也记为σr）作为表征材料疲劳强度的基本指标。在此，N0也称循环基数。

要求零件在无限次（N≥N0）应力循环下不发生疲劳的设计，称为无限寿命设计。此时，应以σr 作为极限应力。要求零件在有限次（N<N0）应力循环下不发生疲劳的设计，称为有限寿命设计。此时，应以有限寿命疲劳极限σrN作为极限应力。

对于疲劳曲线，设计中经常用到的是有限寿命区的高周疲劳段（见图2.3 中的CD 段），利用该段曲线的方程可求得某疲劳寿命N 下的有限寿命疲劳极限σrN，也可求得某个循环应力下的疲劳寿命。式（2.11）即为其拟合方程，称为疲劳曲线方程，即

显然

于是

式中　KN——寿命系数；

　　　m、N0——钢材（材料）：m=6～20，N0=（1～10）×106；中等尺寸零件：m=9，N0=5×106；大尺寸零件：m=9，N0=107。

2）等寿命疲劳曲线

疲劳寿命一定时，不同应力比r 对应的材料疲劳极限σr 也不同，它们之间的关系可用极限应力图表示。如图2.4 所示为σm-σa极限应力图，是极限应力图的表示形式之一，在疲劳强度设计中应用最多，为二次曲线，工程上常用直线近似代替，如图2.5 所示。

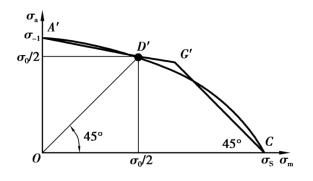
图2.5　材料的极限应力图

在做材料疲劳试验时，通常是求出对称循环及脉动循环时的疲劳极限σ-1和σ0。由于对称循环变应力的平均应力σm=0，应力幅等于最大应力，因此，对称循环疲劳极限在图2.5 中以纵坐标轴上的A′点来表示。脉动循环变应力的平均应力及应力幅均为σm=σa=σ0/2，故脉动循环疲劳极限以由原点O 所作45°射线上的D′点来表示。连接A′、D′得直线A′ D′。因这条直线与不同应力比时进行试验所求得的疲劳极限应力曲线（即曲线A′、D′）非常接近，故用此直线代替曲线是可以的，所以直线A′D′上任何一点都代表了一定应力此时的疲劳极限。横轴上任何一点都代表应力幅等于零的应力，即静应力。取C 点的坐标值等于材料的屈服极限σS，并自C 点作一直线与直线CO 成45°的夹角，交A′D′的延长线于G′，则直线CG′的任一点代表最大应力的变应力状况。

于是，折线A′G′C 即为零件材料（试件）的极限应力曲线，材料中发生的应力如处于OA′G′C 区域内，则表示不发生疲劳破坏；如在区域外，则表示一定发生破坏；如正好处于折线上，则表示工作应力状况已达到极限状态。

图2.5 中，直线A′G′的方程可由已知两点坐标A′（0，σ-1）及D′（σ0/2，σ0/2）按两点式求得，即：

直线A′G′方程为

直线G′C 的方程为

式中　——试件受循环弯曲应力时的极限应力幅和极限平均应力；

　　　φσ——试件受循环弯曲应力时的材料常数，其值由试验及下式决定，即

根据试验对碳钢，φσ=0.1～0.2；对合金钢，φσ=0.2～0.3。

例2.1　某合金钢σ-1=340 MPa，σS=550 MPa。

（1）绘制材料的简化σm-σa极限应力图。

（2）试求r=-0.3 时的疲劳极限σ-0.3。

解　①对于合金钢，通常φσ=0.2～0.3，在此取φσ=0.25。

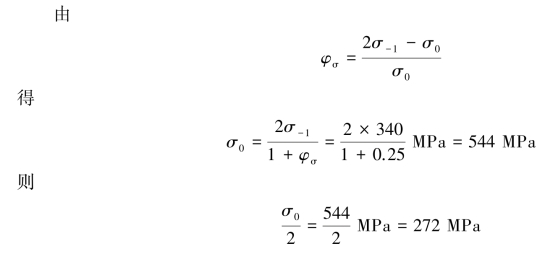
按照图2.5 即可作出材料的简化σm-σa极限应力图，如图2.6 所示。

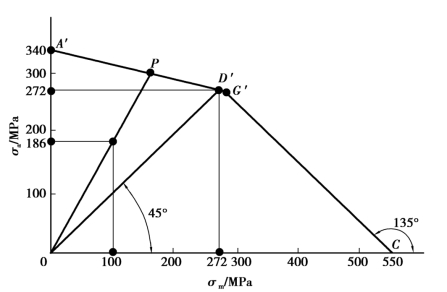
图2.6　例2.1 图

②将σ-1=340 MPa 和φσ=0.25 代入式（2.13）得直线A′D′的方程为

由

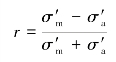
整理得

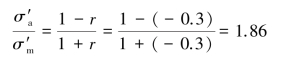
即，代入式（a），解得

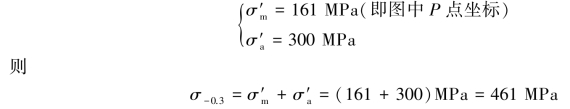
（2）机械零件的疲劳强度计算

1）零件的极限应力线图

由于零件尺寸、几何形状变化、加工质量及强化因素等影响，使零件实际的对称循环弯曲疲劳极限σ-1e要小于材料理论对称循环弯曲疲劳极限σ-1。以弯曲疲劳极限的综合影响系数Kσ 表示材料对称循环弯曲疲劳极限σ-1与零件对称循环弯曲疲劳极限σ-1e的比值，则

若已知Kσ和σ-1可直接求得σ-1e，即

不对称循环时，Kσ 为试件与零件的极限应力幅的比值。将零件材料的极限应力线图中的直线A′D′G′按比例向下移，成为如图（2.7）所示的直线ADG，而极限应力曲线的CG 部分，因是按照静应力的要求来考虑的，故不需进行修正。这样，就得到了零件的极限应力线图AGC。

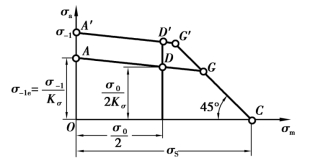
图2.7　零件的极限应力线图

直线AG 的方程：已知点A（0，σ-1/Kσ），点D（σo/2，σo/2Kσ），按两点式求得为

或

直线CG 的方程为

式中　——零件受循环弯曲应力时的极限应力幅；

　　　——零件受循环弯曲应力时的极限平均应力；

　　　φσe——零件受循环弯曲应力时的材料常数。可计算为(www.xing528.com)

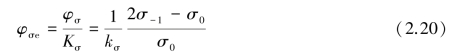
　　　Kσ——弯曲疲劳极限的综合影响系数。可计算为

其中　kσ——零件的有效应力集中系数（下标σ 表示正应力情况）；

　　　εσ——零件的尺寸及截面形状系数；

　　　βσ——零件的表面质量系数；

　　　βq——零件的强化系数。

以上各系数可查阅手册。对于切应力同样可应用上述各公式，只需要用代替σ 即可。

2）单向稳定变应力时机械零件的疲劳强度计算

疲劳强度设计的主要内容之一是计算危险截面处的安全系数，以判断零件的安全程度，安全条件是s≥[s]。下面介绍单向稳定循环应力下安全系数的计算。

机械零件受单向应力是指只承受单向正应力或单向切应力。例如，只受单向拉压或弯曲，只受扭转等。进行零件的疲劳强度设计时，应首先求出零件危险截面上的最大工作应力σmax和最小工作应力σmin，据此计算出工作平均应力σm和工作应力幅σa，然后在极限应力图中即可标示出相应于σm和σa的一个工作应力点M（或者点N），如图2.8 所示。然后，在零件的极限应力线A′D′G 上确定相应的极限应力点。根据该极限应力点表示的极限应力和零件的工作应力，即可计算零件的安全系数。但是，应怎样确定极限应力点呢？这要根据零件工作应力的可能增长规律（是指工作应力随所受载荷的增大而增长的规律）确定。疲劳强度设计中，典型的应力增长规律通常有以下3 种：

①r=C（常数）的情况

如既受弯矩又受扭矩的轴的应力属此例，即

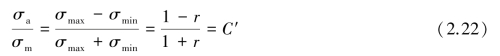
故应力比r=C，即σa/σm为常数。工程设计中，当难以确定零件工作应力增长规律时，一般可按r=C 的规律处理。在此规律下，对应的极限应力的 应与零件工作应力σa/σm相等，为常数。

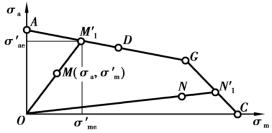
图2.8　r=C 时的极限应力

显然，图2.8 中由坐标原点O 引出的每条射线都代表r=C 的应力增长规律，则极限应力点应在由原点O过工作点M（或N）所引出的射线交极限应力线图上的一点M′和N′。图2.8 中分为两个区：OAG 区为疲劳强度区；OGC 区为屈服强度区。

当工作应力点位于OAG 内时——极限应力为疲劳极限按疲劳强度计算零件的极限应力（疲劳极限）。

OM 线方程

AG 线方程

极限应力：将OM 线与AG 线的方程联解，得交点的坐标为

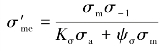
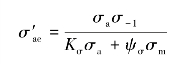
于是

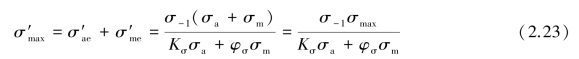
计算安全系数Sca及强度条件

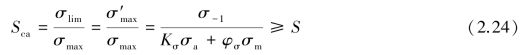
工作应力点（如N）位于OGC 内——极限应力为屈服极限σS，此时，疲劳失效前已产生屈服失效，故仅需进行静强度校核

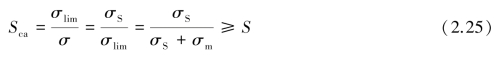
②σm=C（常量）

应力在增长过程中，平均应力保持不变，如车辆的减振弹簧，平均应力由车的质量产生，振动又产生了对称循环应力。此规律下对应的零件的极限应力应与工作应力具有相同的平均应力，即

图2.9 中，过工作应力点M 与横坐标σm轴垂直的直线即代表σm=C 的应力增长规律，其上每个点表示的应力都与工作应力具有相同的平均应力。该直线与零件的极限应力线ADGC 的交点为对应的极限应力点。图2.9 中，OAGH 区为疲劳强度区；HGC 区为屈服强度区。

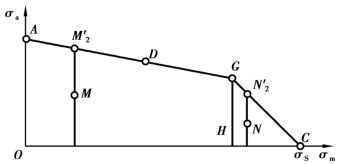
图2.9　σm=C 时的极限应力

如果工作应力点位于OAGH 区（如M 点），那么，将=σm代入AG 的方程式（2.18），可求出零件的极限应力幅，即

则根据最大应力求得的计算安全系数Sca及强度条件为

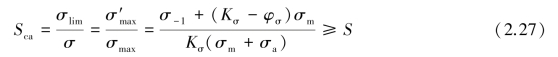
也有文献上建议，在σm=C（常量）的情况下，按应力幅来校核零件的疲劳强度，即按应力幅求得安全系数计算值为

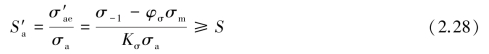
如果工作应力点位于HGC 区（如N 点），则按式（2.24）验算静强度即可。

③σmin=C（常量）

应力在增长过程中最小应力保持不变。如汽缸和液压缸上的联接螺栓，其最小应力由预紧力产生，保持不变。此规律下对应的极限应力应与工作应力具有相同的最小应力，即

在图2.10 中，过工作应力点M（或N），作与横坐标轴夹角为45°的直线即代表σmin=C 的应力增长规律，其上每个点表示的应力都与工作应力具有相同的最小应力。该直线与零件的极限应力线ADGC 的交点为对应的极限应力点。图2.10 中，OJGI 区为疲劳强度区；GIC 区为屈服强度区。

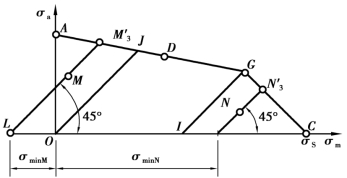
图2.10　σmin=C 时的极限应力

如果工作应力点位于OJGI 区域内时，极限应力在疲劳极限应力曲线AG 上。计算时，所用的分析方法与前述两种情况相同，即可求出点对应的零件的极限平均应力和极限应力幅为

据此可推导出分别按最大应力和应力幅计算的安全系数及安全条件（推导过程省略）为

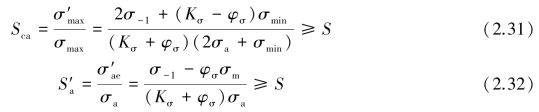
当工作应力点位于GIC 区域内时，极限应力统为屈服极限，故只需按式（2.24）进行静强度计算。

对于剪切变应力，只需把以上各公式中的正应力符号σ 改为切应力符号即可。

以上3 种应力增长规律下的安全系数计算均属无限寿命设计。如果是零件疲劳寿命在104<N<N0的有限寿命设计，则上述分析过程和公式中用到的各σ-1和σ0须换成N 次循环下的条件疲劳极限σrN，即统一按式（2.2）求出的σrN来代替σr（以σ-1N代替σ-1，以σ0N代替σ0）而其他的不变。显然，这时零件的计算安全系数就会增大。

例2.2　某零件危险截面上的平均应力为σm=180 MPa，应力幅σa=95 MPa。材料为合金钢，σ-1=400 MPa，σS=520 MPa，疲劳缺口系数Kσ=1.55，尺寸系数εσ=0.75，表面状态系数β=0.9，取许用安全系数[S]=1.5。用解析法和图解法求零件的安全系数，并判断其安全性。

解　题中没有指明零件的应力增长规律，则可按r=常数的规律计算。

1）解析法求安全系数

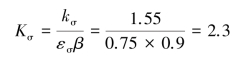
材料为合金钢，取φσ=0.25，由式（2.24）计算安全系数为

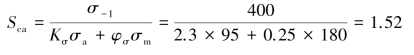
2）图解法求安全系数

由此按图2.5 作出零件的σm-σa图，如图2.11 所示。在图中描出工作应力点N（180，95），作射线ON 交AD 于点。

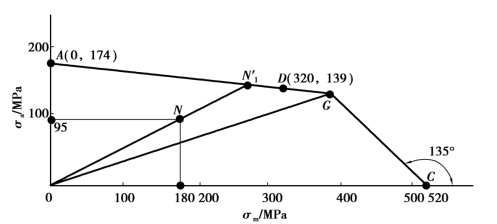
图2.11　例2.2 图解

由图2.11 可直接量出线段和ON 的长度，则零件的安全系数为

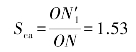
显然，满足安全条件Sca>[S]，故零件是安全的。