模拟数据和数字信号在通过某一介质传输时,往往要进行调制和编码,以提高信号的传输性能。调制就是用基带信号对载波波形的某些参量进行控制,使这些参量随基带信号变化。载波信号通常为高频信号,任何载波信号均有3 个特征: 振幅(A)、频率(F)和相位(P)。与之相应,调制技术涉及载波信号的振幅、频率和相位的一个或几个参数的变化,即振幅调制、频率调制、相位调制或多重调制。无论基带信号是模拟数据还是数字数据,经过调制后就作为模拟信号通过模拟通信系统来传输,并在接收端解调,转换成原来的形式。调制的目的有: 当无线传输时,高频信号易于辐射;便于频分多路传输,以便提高线路利用率。根据载波形式不同,调制可以分为正弦波调制和脉冲调制两大类。
编码是将模拟数据或数字数据转换成数字信号,以便通过数字通信介质传输出去,在接收端,数字信号通过译码转换回原来的形式。根据任务不同,编码可分为3 种形式: 一是为提高可靠性而采取的差错控制编码或抗干扰编码;二是为数字传输将模拟信号通过A/D 转换化为数字信号或为提高数字信号有效性而进行的编码,这类编码措施称为信源编码;三是为了通信保密,在信源编码后对信号加密,而在相应的接收端解密成为保密编码。在计算机网络中,由于传输的需要,数据信号必须进行调制或编码,使其与传输介质及协议相适应。通常有4 种数据的调制和编码方法: 模拟数据的模拟调制、数字数据的模拟调制、数字数据的数字编码和模拟数据的数字编码。
1.模拟数据的模拟调制
模拟数据经由模拟通信系统传输时不需要进行变换,但考虑到无线传输和多路传输的需要,模拟形式的输入数据可在其高频正弦波下进行模拟调制。模拟调制有幅度调制、相位调制和频率调制技术。最常用的两种调制技术是幅度调制和频率调制。假设高频正弦波函数为f(t)=Asin(Ft +P),通过调整振幅(A)、频率(F)和相位(P),可以得到不同的波形。
幅度调制是指载波的幅度会随着原始模拟数据的幅度做线性变化的过程。因此,载波的幅度会在整个调制过程中变动,而载波的频率是相同的。通信系统在接收到幅度调制的信号后,通过解调,可恢复成原始的模拟数据,如图1-6-2 所示。
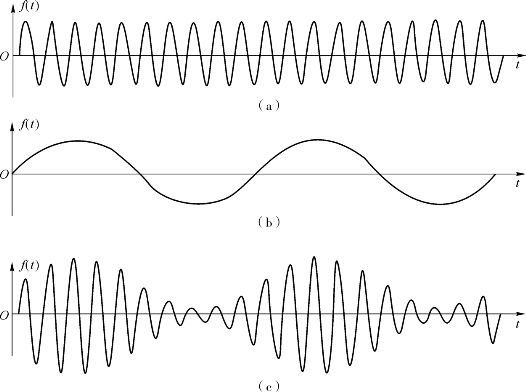
图1-6-2 幅度调制
(a)载波;(b)调制信号(基带信号);(c)调幅波
频率调制是指高频载波的频率会随着原始模拟信号的幅度变化而变化的过程。因此,载波频率会在整个调制过程中波动,而载波的幅度是不变的。通信系统在接收到频率调制的信号后,进行解调,以恢复原始的模拟数据如图1-6-3 所示。
2.数字数据的模拟调制
在使用模拟传送数字信号时,需要借助调制解调装置,把数字信号调制成模拟信号,使其变为适合于模拟通信线路传输的模拟信号。经过调制的信号称为已调信号。通信系统将已调信号通过模拟通信线路传输到接收端,在接收端将已调信号解调还原为数字信号。数字信号的模拟调制有3 种调制技术: 幅移键控法(Amplitude-Shift Keying,ASK)、频移键控法(Frequency-Shift Keying,FSK)和相移键控法(Phase-Shift Keying,PSK)。3 种调制技术的基本波形如图1-6-4 所示。
1)幅移键控法

图1-6-3 频率调制
(a)载波;(b)调制信号(基带信号);(c)调频波

图1-6-4 3 种调制技术的基本波形(https://www.xing528.com)
幅移键控法就是用数字基带信号来控制正弦波载波信号的振幅。在幅移键控方式下,通常用载波频率的两个不同的幅度来表示二进制的两个数,即0 和1。当传输信号为1时,幅移键控信号的振幅保持某个电平不变,即有载波信号发射;当传输信号为0 时,幅移键控信号的振幅为0,即没有载波信号发射。由图1-6-4 可以看出,幅移键控法实际上相当于用一个受数字基带信号控制的开关来开启和关闭正弦波信号。幅移键控法可用于通过光纤传输数字数据,如果发送器为发光二极管,则有光表示一个信号,无光表示另一个信号。
2)频移键控法
频移键控法就是用数字基带信号来控制正弦波信号的频率。由图1-6-4 可以看出,在频移键控方式下,通常用载波附近的两个不同频率来表示二进制数的两个值,即0 和1。频移键控方式比幅移键控方式更不容易受干扰。在话音线路上使用频移键控法,传输速率可达1200 bps。这种方式一般用于高频(3 ~30 MHz)的无线电传输,它甚至能用于较高频率传输的同轴电缆局域网。
3)相移键控法
在相移键控中,二进制的0 和1 是通过载波信号的相位偏移表示的,相移键控法就用数字基带信号来控制载波信号的相位。由图1-6-4 可以看出,可通过调整载波的相位来表示不同的二进制值。相移键控可以分为绝对相移键控和相对相移键控。
3.数字数据的数字编码
数字数据的数字编码是指将数字数据用物理信号(如电信号)的波形表示。通常,可以用许多不同形式的电信号的波形来表示数字数据。数字信号是离散的、不连续的电压或电流脉冲序列,每个脉冲代表一个信号单元(或称码元)。这里所说的数字信号主要是二进制数据信号,也就是用两种码元形式分别代表二进制数0 和1,每一位二进制符号和一个码元相对应。采用不同的编码方案,产生出的表示二进制码元的形式也不同。
目前,数字数据的数字编码主要采用不归零码、归零码和曼彻斯特码。这三种编码各有优缺点,选择应用时应注意以下问题:
(1)脉冲信号的宽度越大,发送信号的能量也就越大,这对提高接收端的信噪比有利。
(2)脉冲时间宽度与传输频带宽度成反比关系,归零码的脉冲比不归零码窄,因此在信道上占用的频带较宽;归零码在频谱中包含了码元的速率,即在发送信号的频谱中包含有码元的定时信息。
(3)双极性码与单极性码相比,直流分量和低频分量减少了,如果数据序列中1 的位数和0 的位数相等,则双极性码没有直流分量输出,交替双极性码也没有直流分量输出,这一点在实际传输中是有利的。
(4)曼彻斯特码和差分曼彻斯特码在每个码元中均有跃变,没有直流分量,利用这些跃变可以自动计时,因而便于同步。在编码中,曼彻斯特码和差分曼彻斯特码的应用很广泛,已成为局域网的标准编码。
4.模拟数据的数字编码
用数字信道传输模拟数据时,通常对模拟数据进行脉冲编码调制(Pulse Code Modulation,PCM),PCM 通过取样、量化和编码3 个步骤,将模拟信号转变成数字信号。所谓取样,就是从模拟信号中提取样本信息,即按照一定的时间间隔采样模拟信号的幅值。根据采样定理,只要取样频率不低于模拟信号带宽的2 倍,就可以从取样的脉冲信号中无失真地恢复原来的模拟信号。例如,普通话音信号的带宽为4 kHz,那么采样的频率可以取8 kHz。所谓量化,就是将取样点处取得的信号幅值分级取整的过程,即将取得的模拟信号的最大幅值等分为若干等级(为了编码方便,通常为2n 级)。所谓编码,就是将量化后的整数值使用二进制数来表示。图1-6-5 所示为量化和编码的过程。
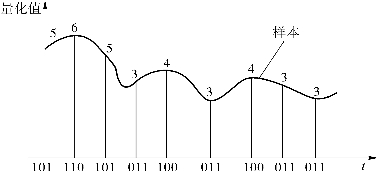
图1-6-5 量化和编码的过程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




