天津大学水利水电系课题组成员以拉西瓦拱坝为工程背景，采用加重橡胶，建立了大比尺（1∶100）的水弹性模型，全面模拟了“坝体-地基-库水-动荷载”四位一体流固耦联的振动系统。同时要求满足“动荷载”输入系统相似和结构系统动力响应相似，即要求满足水力学条件和结构动力学条件相似。水弹性模型的制作工艺和模拟范围详见文献[16，17]。
为了能够较好测试拱坝模态，在顶拱布置了13个动位移响应测点，如图14.15所示。考虑到拱坝振动响应主要以径向振动（R方向）为主，切向振动（S方向）和垂向振动（Z方向）相对较小，因而振动响应测试以量测R方向的振动为主。
试验采用具有耐冲击和高稳定度的DP型地震式低频振动传感器（DSP—0.35—20—V）进行测试，在某工况下，采样频率为100Hz，观测信号{y i}包含13个通道，即所构成的Hankel矩阵行块中，每一块包含13行数据，图14.16是采集到的A-0号测点的位移时程，对该拱坝进行模态参数识别。结构模态阶次的确定由图14.17所示的奇异熵增量谱可知，当奇异熵增量ΔEi≤0.05，即系统阶次i=16时，奇异熵增量就已经增长缓慢，并趋于平稳，说明信号的有效特征信息量已经趋于饱和，特征信息已经基本完整，之后的奇异熵增量可认为是宽频带噪声所致，可以不予考虑。根据复模态理论，剔除系统的非模态项（非共轭根）和共轭项（重复项）之后，系统的模态阶次为[i/2]=8阶，剔除噪声引起的虚假模态影响，最终识别出该拱坝结构前5阶模态频率、阻尼比和振型，频率稳定图如图14.18所示。
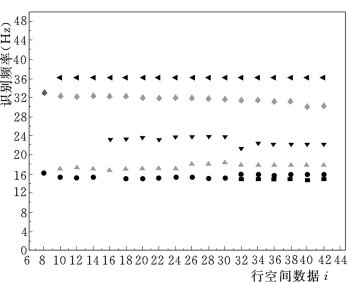
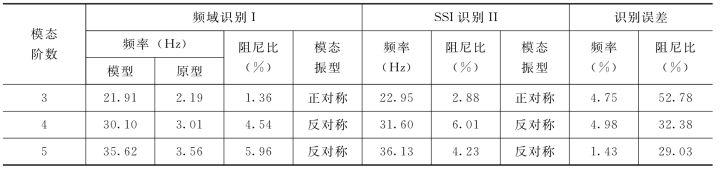
由图14.18的稳定图可知，识别频率随着行空间行数的增加而有所浮动，对所有各阶模态频率进行均值处理后，得到稳定的识别结果；同理，对阻尼比和振型的识别也进行均值后得到各阶稳定的阻尼比和振型。为检验本文方法识别结果的有效性和准确性，同时采用冲击锤击振方法，对满库工况下拱坝进行单点激振、多点拾振的频域测试。选取D-1点为激振点，对获得的激励和响应信号进行分析处理，通过传递函数的曲线拟合识别出水弹性模型的模态参数。记方式I为冲击锤击振下模态参数识别，方式II为泄洪激励下模态参数识别，频率、阻尼比及模态振型识别结果见表14.6，振型识别结果对比如图14.19所示。
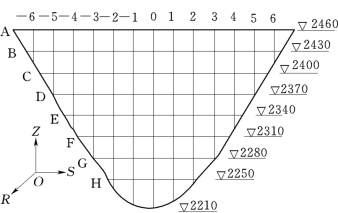
图14.15 测点布置图
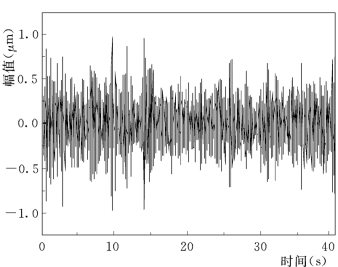
图14.16 A-0号测点的位移时程
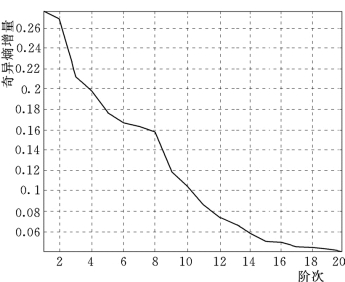
图14.17 奇异熵增量谱
(www.xing528.com)
图14.18 频率稳定图
从识别结果可以看出，两者频率识别结果非常接近，误差均在5%以内，低阶模态频率识别结果更为精确，满足工程要求精度；阻尼比的偏差值在某些情况下要达到40%以上，这主要是因为目前人们对阻尼的认识还不够彻底，还存在很多模糊的地方，在计算和理论分析时，只是采用了几种假定的阻尼形式；振型的识别结果比较理想，两种方法的识别结果基本趋于一致。
表14.6 频域方法与随机子空间方法识别结果的对比
续表
注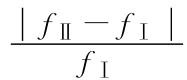 
×100%为频率误差，
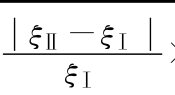×100%为阻尼比误差。
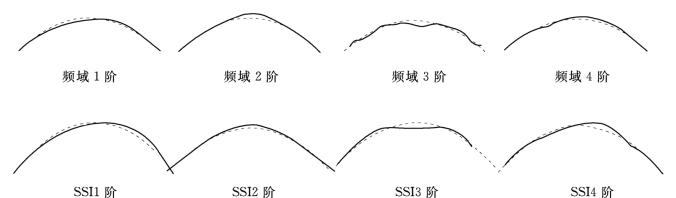
图14.19 频域、SSI振型识别结果对比
（图中实线为振型振动位置，虚线为平衡位置）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
