二滩拱坝模态参数识别优化方法

2004年、2005年对二滩拱坝泄洪振动进行原型观测，在坝顶布置10个测点，如图14.2所示，1号、9号测点动位移时程曲线如图14.3所示。首先对所采集的原始信号进行降噪处理，并计算各测点在不同工况下的奇异熵增量随阶次的变化，计算结果表明奇异熵增量在20阶以后趋于稳定，如图14.4所示，前20阶足以包含信息的特征量，信号降噪重构前后对比（局部放大）如图14.5所示。信号通过降噪重构后用NEx T法计算9号点相对1号点的互相关函数，如图14.6所示，以此作为脉冲响应函数进行参数识别。脉冲响应信号的奇异熵增量随阶次变化如图14.7所示。当奇异熵增量开始降低到渐进值时，奇异谱阶次可确定为7阶，此时信号的有效特征信息量已趋于饱和，特征信息已基本完整。对系统矩阵A进行特征值分解后，剔除特征值中的非模态项（非共轭根）和共轭项（重复项），实际得出大坝泄洪振动的工作模态阶数为3阶（表14.1）。结果表明：拱坝存在一定的“拍”振现象（图14.2），主要由于大坝的第一、第二工作频率较为密集（分别为1.5Hz、1.6 Hz左右），加上水流荷载激励也处于该频带范围内，为形成“拍振”提供了条件，而其他频率振动的能量显得弱小[15]。

表14.1　二滩拱坝在各工况下坝体工作模态参数的识别结果

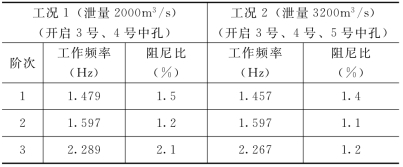
图14.2　二滩拱坝原型动位移的测点布置

图14.3　1号、9号测点动位移的时程曲线

(www.xing528.com)

图14.4　原始信号的奇异熵增量随阶次变化

图14.5　信号降噪后的重构

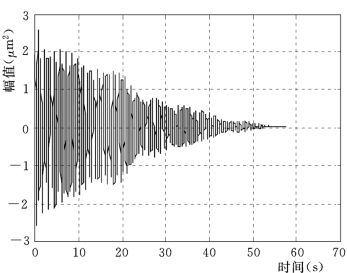
图14.6　NEx T法提取9号点的脉冲响应

图14.7　脉冲响应的奇异熵增量随阶次变化