随机子空间方法的优化应用

以随机子空间法为基础的各种辨识方法（Stochastic Subspace Identification，SSI），是当前利用环境激励去进行模态参数识别的最为精确的方法之一，它直接作用于时域数据，不必将时域数据转换为相关函数或谱，避免了计算协方差矩阵[8]。该方法采用有效的数学处理方法去识别离散后的系统状态空间矩阵，从而得到系统的动力学特性参数，其特征为总体识别，有较高的识别精度。

1.结构振动的随机状态空间模型

水工结构在水流激励下的响应可以用以下运动方程来表示：

式中：M、C1、K∈Rn1×n1分别为质量、阻尼和刚度矩阵；n 1为系统自由度数；¨q（t）、˙q（t）、q（t）∈R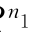×1分别为连续时间t时刻的加速度、速度和位移向量；B∈R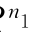×m为系统输入矩阵，表示激振力的位置；u（t）∈Rm×1为时间输入向量；m为激励点数。

对方程式（14.37）分别进行引入系统状态向量、数据截断与数据离散，加入随机分量（噪声）后，可以得到离散时间随机状态空间模型：

式中：k为采样点序号；x k∈Rn×1为在kΔ时刻系统的状态向量；n为两倍系统自由度数，n=2n1；Δ为采样时间间隔；uk为输入向量；y k为输出向量；A∈Rn×n、B∈Rn×m、C∈Rm×n、D∈Rm×m分别为离散的系统矩阵、控制矩阵、输出矩阵和传递矩阵；w k、v k分别为系统不确定性的过程噪声和测量噪声。

实际上很难准确确定各自的过程噪声和测量噪声的特性，假定噪声为零均值的白噪声且其协方差矩阵满足：

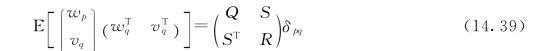
式中：E为数学期望符号；δpq为Kronecker delta函数，即对于p和q任意两个时间点，满足p=q⇒δpq=1，p≠q⇒δpq=0。

在实际测量过程中，水流激励是不可测量的随机激励，而且其强度基本和噪声影响相似，因此，将式（14.38）中的输入项uk和噪声w k、v k合并，从而得到纯随机输入的离散状态空间方程：

2.随机子空间算法的原理[9]

对结构进行检测时，假定有m个测点，每个测点数据长度为j。将测点响应数据组成2mi×j的Hankel矩阵，它包含2i块的行和j列，每块有m行，根据统计序列原理，当j/i足够大时，可以认为j→∞。把Hankel矩阵的行空间分成“过去”行空间和“将来”行空间：

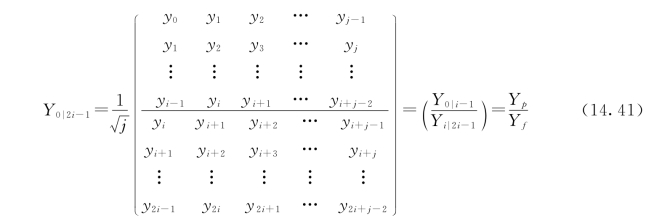
式中：y i表示第i时刻所有测点的响应；下标p表示“过去”；下标f表示“将来”；Y 0|i-1表示Hankel矩阵中第一行的下标起始时刻为0、终点时刻为i-1的所有测点组成的Hankel矩阵的块。

对Hankel矩阵进行QR分解来进行数据缩减：

式中：R∈R 2mi×j是下三角矩阵；Q∈Rj×j是正交矩阵；R 11、R 21、R 22∈Rmi×mi；Q T1、Q T2∈Rmi×j，Q∈R（j-2mi）×j。

根据投影理论，Y f的行空间在Y p形成的行空间上的正交投影矩阵为：

式中，（Y p Y）+为矩阵的Moore-Penrose伪逆，因而根据过去的数据信息可以预测将来的数据信息。或利用式（14.42），投影矩阵可以用更简洁的表达式：

根据随机子空间识别理论，投影矩阵Oi可以分解为可观矩阵Γi与卡尔曼滤波状态向量i的乘积：

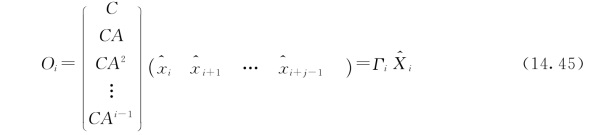
卡尔曼滤波状态序列的目的是利用已知的直到k时刻的输出序列、系统矩阵和噪声的协方差矩阵，得到k+1时刻状态向量x k+1的最优估计，用x^i+1表示。详见文献[10]。

为得到可观矩阵Γi与卡尔曼滤波状态向量X^i，对投影矩阵Oi进行奇异值分解（SVD）：

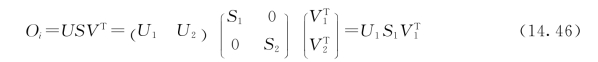
式中：U 1∈Rmi×n，S1∈Rn×n，S2=0，V∈Rn×j。如果系统是可观与可控的，非零奇异值的个数，即矩阵S 1的秩就是投影矩阵的秩。有式（14.45）和式（14.46）可得可观矩阵Γi与卡尔曼滤波状态向量i：(www.xing528.com)

同理，有式（14.45）可以得到下一时刻的投影：

Γi-1的值可以将Γi的最后m行去掉得到。相应的卡尔曼滤波状态向量为：

由式（14.47）和式（14.49）得到的卡尔曼滤波状态向量和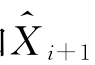，此时的状态空间方程为：

式中，Y i|i∈Rm×j是只有一个块行的Hankel矩阵，W i、V i是残差。由于卡尔曼滤波状态向量和输出已知，且残差矩阵与估计序列X^i不相关，因此可以通过最小二乘法求解式（14.50）线性方程组，得到系统矩阵A和输出矩阵C：

3.模态参数的提取

对系统的状态矩阵A进行特征值分解：

式中：λi为离散时间的特征值；ψ为系统的特征向量矩阵，ψ∈Cn×n。

根据离散时间系统与连续时间系统的特征值关系：

模态特征值λci、λ与系统固有振动圆频率ω、阻尼比ξ的关系为：

模态振型可表示为：

由此可见，只要识别出了系统矩阵A和输出矩阵C就可以提取出结构的模态参数（频率、阻尼比和振型）。

4.噪声模态的剔除

基于虚假模态对不同参数模型比较敏感易变的原则，通过考察一些不同的参数模型，那些同时出现次数最多的、稳定的模态可以认为是系统的真实模态[11-12]。本文借助于稳定图对噪声模态进行剔除，有关文献[13]认为把系统的阶次由n min增加到n max，把计算得到的结果画到二维坐标图中（横坐标为频率值，纵坐标为阶次），便可得到稳定图，这样虽然可以得到系统的模态参数，但没有考虑Hankel矩阵的行空间数据变化对结果的影响，从而参数识别的精度不高且无法得到系统的阶次。

针对SSI具有Hankel矩阵的维数较难确定、可能丢失模态或产生虚假模态的缺点，本文对稳定图剔除噪声模态的方法进行如下改进：

（1）在利用奇异熵增量谱确定系统的模态阶次后，把Hankel矩阵的行空间数据由i min增加到i max时（i max是个相对的较大值，要满足j/i足够大），把计算得到的结果画到二维坐标图中（横坐标为频率值，纵坐标为Hankel矩阵的行块数），从而得到模态参数的稳定图。

（2）在稳定图中若相邻两点的频率和阻尼比在容许误差范围内，则认为是相同的。

（3）可以根据所测试结构的具体情况加入阻尼比的判据准则，例如，结构阻尼比值通常大于10%或小于1%时，可以认为是虚假模态。

（4）为了得到更为精确的识别结果，利用模态置信因子MAC指标进行虚假模态的判别，其中MAC是从振型相关性角度来区分噪声模态的，它们的值介于0～1之间，当为系统真实模态时，MAC→1，当为噪声模态时，MAC→0。模态置信因子的详细表述见文献[14]。

经过以上四步改进，得到更为精确的稳定图。在此，提出用“三步法”对模态参数进行更为精确的识别：第一步，用奇异熵增量对系统进行定阶，使得定阶的界线更加清晰和稳定；第二步，在系统阶次明确的前提下，利用改进的稳定图对虚假模态进行剔除，使得参数识别的结果更为准确可靠；第三步，将各阶模态参数识别结果进行平均处理，最终得到更为精确的识别结果。模态参数识别流程如图14.1所示。

图14.1　模态参数的识别流程