弧形闸门在水电工程中有着广泛的应用,并在运行中发挥出极其重要的作用。在设计方面一直受到国内外专家们的高度重视,以期找出一种行之有效的设计方法,设计出既安全可靠,又经济实用的闸门来。主框架是弧门的主要承重结构,重量一般占闸门自重的60%~70%,其安全、经济与否决定着整个弧门的安全和经济。以往的设计是凭经验先拟定截面尺寸,然后进行强度、稳定和刚度等校核。这样设计出的主框架往往不够经济,而且需多次复重设计。本节以主横梁式弧门主框架为依托,在考虑支臂的动力稳定性的基础上对弧形闸门主框架进行结构优化。
13.2.1.1 闸门主框架结构的优化数学模型[4-5]
主横梁式弧形闸门的主框架型式主要有三种型式,即π形、П形和斜支臂框架,其中π形和П形均为斜支臂框架的特殊情况。建模时以如图13.6所示的斜支臂、箱形截面来进行优化设计。
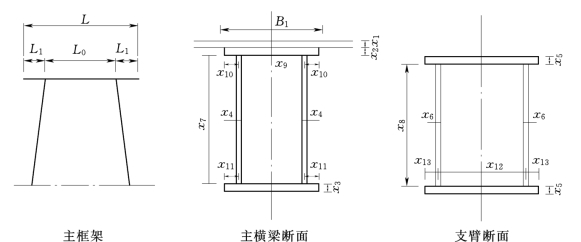
图13.6 支臂主框架及其断面
1.设计变量
设计变量包括主横梁和支臂断面尺寸共13个,如图13.6所示
![]()
式中:i表示第i个设计方案;x 1为面板厚度;x 2为主梁上翼缘厚度(靠近面板处);x 3为主梁下翼缘厚度;x 4为主梁腹板厚度;x 5为支臂翼缘厚度;x 6为支臂腹板厚度;x 7为主梁腹板高度;x 8为支臂腹板高度;x 9为主梁腹板间距;x 10为主梁上翼缘外延长度;x 11为主梁下翼缘外延长度;x 12为支臂腹板间距;x 13为支臂翼缘外延长度;B1为面板有效宽度。
2.目标函数
以主框架重量为目标函数,包括主横梁和支臂,可表示为:
![]()
式中:W 1(x)为主横梁重量;W 2(x)为支臂重量。
按照DL/T 5039—1995《水利水电钢闸门设计规范》规定,面板与主横梁翼缘连接时,应考虑面板参与主横梁的翼缘工作,其有效宽度B 1根据规范确定,因此目标函数可以表示为:
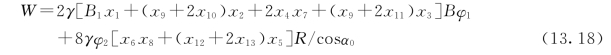
式中:γ为钢材的比重,取0.0078kg/cm3;B为弧门宽度;R为弧门半径;φ1、φ2分别为主横梁、支臂考虑加劲肋时的重量增加系数,取1.1~1.2;α0为支臂倾斜角度。
13.2.1.2 闸门主框架结构的约束条件
1.静力约束条件
(1)强度约束。强度验算包括主横梁和支臂控制断面的正应力和剪应力验算,支臂按偏心受压构件处理,其约束条件为:

式中:N为验算截面轴力;A为验算截面面积;M为验算主横梁截面处弯矩;W为验算截面最小抵抗矩;Q为验算截面处剪应力;S*为验算剪应力处以外截面面积对中性轴的面积矩;I为验算截面对中性轴的惯性矩;t为腹板厚度;[σ]为容许正应力,[τ]为容许剪应力。
(2)刚度约束。根据规范规定,主梁满足强度和稳定的同时,也应该同时满足刚度的要求,其刚度验算按两端带悬臂的简支梁承受均布荷载计算,最大挠度位于跨中。对于支臂限制其在主框架平面内和主框架平面外的长细比λx、λy不大于120。约束条件为:

式中:f max为主横梁跨中最大挠度;[ ]为容许相对挠度,潜孔式工作闸门和事故闸门取1/750,露顶式闸门取1/600。
]为容许相对挠度,潜孔式工作闸门和事故闸门取1/750,露顶式闸门取1/600。
(3)稳定性约束。稳定性验算应该包括整体稳定性和局部稳定性验算。
1)支臂的整体稳定性验算:由于主框架是一个空间结构,因此支臂整体稳定性包括主框架平面内和主框架平面外的稳定性,其约束条件为:

式中:φx、φy分别为主框架平面内、外的稳定系数;η、φb为截面调整系数。
2)局部的稳定性验算:局部稳定性约束主要包括主横梁和支臂的腹板以及受压翼缘的局部稳定。
腹板的局部稳定约束条件为:
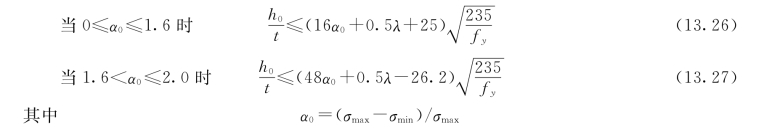
式中:h 0、t分别为腹板的高度和厚度;σmax为腹板计算高度边缘的最大压应力;σmin为腹板计算高度另一边缘相应的应力;λ为计算构件在弯矩作用平面内的长细比;f y为材料的屈服极限,不同的钢材取不同的值。(https://www.xing528.com)
对于箱形截面其受压翼缘的局部稳定约束条件为:
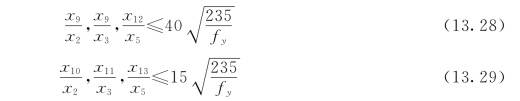
(4)几何约束。几何约束主要是对结构构造方面的要求,有:
![]()
式中:x i max、x i min分别为设计变量x i的上限和下限。
2.动力约束条件
工程上大量工作弧形闸门的失事主要是由于动荷载作用下弧形闸门支臂动力失稳而破坏的,在进行结构优化时,不仅要使弧门支臂满足静力刚度要求,而且还要保证支臂在动力荷载作用下的动力稳定。偏心荷载作用下支臂的动力稳定性在前一章中已讨论,考虑偏心荷载作用下支臂的动力稳定性作为动力约束条件更具一般性。
支臂满足动力稳定实质上就是使支臂远离图13.7中的动力不稳定区域,由方程可以确定支臂处于动力稳定区域的主要约束条件(也即动力约束条件)为:
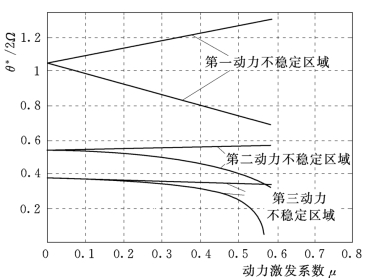
图13.7 偏心荷载作用下支臂参数振动的动力不稳定区域
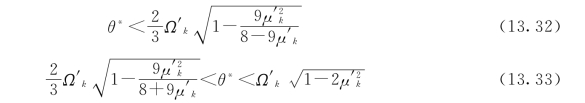
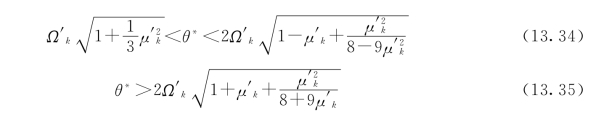
在激振力频率θ*已知的情况下,支臂横向振动频率Ω只要满足式(13.32)、式(13.33)、式(13.34)、式(13.35)中的任意一项,就可以保证支臂的动力稳定。换句话说,也就是要求支臂的自振频率(或刚度)满足一定的要求。
13.2.1.3 主框架结构计算
1.主框架分布荷载p
对于露顶式弧形闸门当上游水位为H S时,其单位宽度上承受的静水压力p为:
![]()
p与水平线的夹角为:
![]()
当支铰位于上游水位以上时,p x、p y分别为:
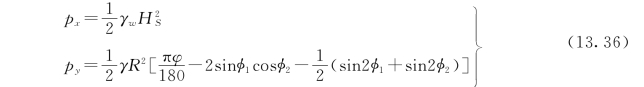
总水压力分布在上、下主框架上的均布荷载qu、qd可以由下式求得(荷载简化如图13.8所示):
![]()

图13.8 主框架荷载
2.主框架内力计算
用轴线代替主横梁和支臂构件,计算简图如图13.9所示,以下支臂所在的主框架为典型计算框架,用结构力学法可以求得控制断面内力和位移如下:
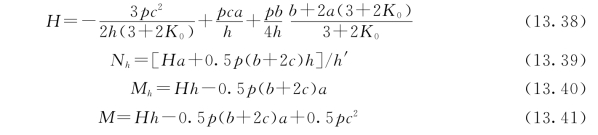

图13.9 主框架内力图
式中:K 0为主横梁和支臂单位刚度比;H为主横梁轴力(压为正);N h为支臂轴力(压为正);M h、M、M l如图13.9所示;f max为主横梁最大挠度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




