闸门振动稳定性计算、实验结果与拍振原因分析

闸门振动稳定性计算分以下两种情况。

（1）已知闸门运行上下游水位判定其稳定性。图12.13给出了闸门在不同水位条件下的振动衰减率（λ的实部）的计算结果。

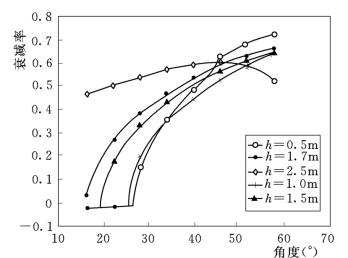
图12.13　闸门振动的衰减率

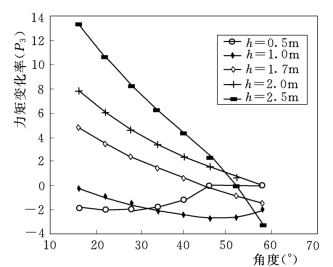
图12.14　下游水压力的变化率

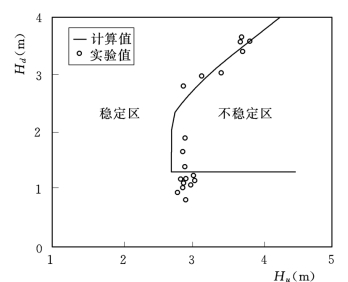
结果表明：在下游水位较低时，即自由出流或淹没度小的淹没出流条件下，闸门振动的衰减率在部分区域（角度）出现正值为“不稳定区”，同时在其他部分区域出现负值为“不稳定区”或“抑振区”。当“抑振区”存在时，闸门不稳定性振动发展到一定范围内就受到抑制，限制了“拍振”的形成。随着下游水位的增高，闸门振动衰减率在各运行区域皆为正，即当闸门受到开门方向的扰动之后，闸门将向开门方向运动，直到闸门撞击支墩。相反当闸门受到关门方向的扰动后，闸门将向关门方向运动直到撞击底坎，这样就形成“拍振”。图12.14给出了下游水压力力矩随开度的变化率。可见在下游水位较低时，力矩变化率为负，即闸门开度增大开门力矩减小，这对振动有抑制作用。随着下游水位的升高，力矩的变化率逐渐由负转为正，即闸门开度增大开门力矩也增大，这使振动扩大，不利于闸门的振动稳定。图12.15给出了上游水压力力矩随开度的变化率，其值为负，说明上游水压力对闸门振动不稳定性有抑制作用，因而可以认为下游压力的作用是形成闸门拍振的主要因素。图12.16给出了闸门在不同运行水位条件下闸门稳定性的计算和实验结果，两者吻合较好。由该结果可得闸门形成拍振包括以下几点：①下游淹没水位高于某一临界水位值H dc；②上、下游水位存在一定水位差ΔZ；③上游水位大于某一临界水位H uc，理论计算给定了闸门运动“稳定区”和“不稳定区”。对于本算例（3m×6m翻板闸门）下游临界水位H dc的计算结果为1.3m，实验结果平均值为1.15m，上游临界水位H uc的计算和实验值都约为2.6m，闸门形成拍振一般至少需存在20cm的水位差。

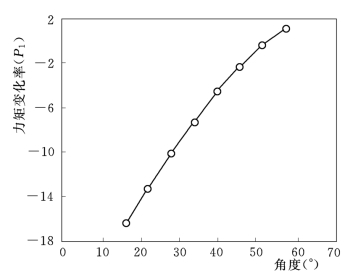
图12.15　上游水压力的变化率

(www.xing528.com)

图12.16　稳定性的计算和实验结果（已知上下游水位）

（2）已知过流流量Q和下游水位H d（或者是河道水位流量关系），推求闸门运行的上游水位和在该水位条件下的稳定性特征。在此条件下求闸门稳定性还需已知淹没出流条件下流量与上游水位，下游水位及闸门开度的关系：

式中：m为薄壁堰流量系数；σ为闸门倾斜修正数；h w为门顶水头；H 0门前水深；m孔为闸孔流量系数；σs为淹没系数；e为孔高。本文计算中流量系数由实验修正。

再根据闸门在某一定开度条件和下游水位受力平衡条件：

联立式（12.102）、式（12.103）可推求闸门在某一流量和下游水位条件下的运行角度和上游水位。有了上、下游水位条件即可判定闸门的稳定性状态。一般来说，大流量时，闸门平衡开度也大，而闸门开度增大时，上游水位下降。从闸门稳定性条件可知，闸门形成拍打必须保证总力矩的平均为正，即上游水位应高于下游水位一定数值，上游水位下降就意味着形成拍打的下游水位下降，即拍打区缩小。随着流量进一步增大，拍打区会进一步缩小。从稳定性计算结果表明当上游水位下降到一定程度后，任何在下游水位下，闸门都是稳定的。因而可以认为流量大于某一数值Qc后，闸门不形成拍打是可能的。图12.17给出了不同流量条件下，闸门运行的“稳定区”和“不稳定区”的计算和实验结果。本算例在Q大于25m3/s时，任何上下游水位条件下不会出现拍打。

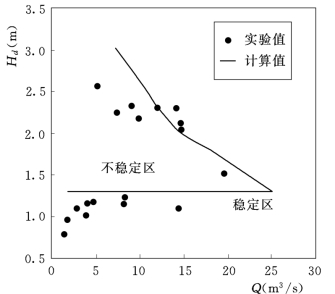
图12.17　稳定性的计算和实验结果（已知流量和下游水位）

综上所述，可以得出以下结论：翻板闸门运行过程，可能存在三种不同类型振动：微幅随机振动、有限范围不稳定振动和大幅度“拍振”，后两种型式的振动直接与闸门和水流耦联系统的稳定性特征有关。以上提出理论模型可较好地预报闸门系统的稳定性特征，计算和实验表明下游水压力作用是形成“拍振”的主要因素，闸门形成“拍振”的必要条件可归结以下几点：①下游水位高于某一临界值；②上游水位不低于某一临界值；③上、下游水位差大于某一临界值；④流量小于某一临界值。根据以上条件可设计出无危害性振动（拍振）的水力自控闸门。