闸门的稳态自激响应分析

12.1.3.1 平面闸门稳态自激机理的回顾

1.平面闸门的垂向振动

对于平面闸门垂向振动，Hardwick[1]进行了系统的实验研究，认为闸门底缘自由剪切层破坏形成的漩涡造成主流向闸门底缘附着的瞬时条件，这种不稳定的重附着使作用于闸门底缘的流体力产生周期性的变化，在某种特定条件下，流体力与闸门处于共振状态，即产生了自激振动。Kolkman和Vrijer[2]阐述了闸门垂向振动的流体惯性模式，认为在闸门振动过程中，闸孔有效过水面积的变化导致了流量的脉动。流量的脉动及其惯性在孔口局部产生压力差的变化又引起了作用在闸门上动水压力的变化，同时也影响流量的脉动。Thang和Naudascher[3]用驰振理论解释了闸门垂向振动的物理机制，认为闸门运动而产生的流线分离，在闸门底缘产生附加的吸引力。这个力与闸门运动速度同方向，故会使闸门的振动加剧。对于引起闸门垂向振动是流体惯性机制还是驰振机制的问题，Koldman与Thang和Naudascher展开了讨论[4]，后来，Kanne[5]等人进一步阐述了流体惯性机制和驰振机制，认为两者是同时存在的，只是不同条件下强弱不同。

2.平面闸门的顺流向振动

对于平面闸门顺流向振动（主要是顺流向弯曲振动），一般可分为两种情况。

（1）第一种情况，当闸门面板与底板呈斜交时，闸门顺流向振动将导致流量脉动，以致压力脉动，由此产生持续的自激振动响应。Ishii[6]研究表明，闸门振动诱发流体反馈力包括两个方面，由流量交变引起压力脉动，它将给闸门振动提供能量。

（2）第二种情况，当闸门面板与底板正交时，闸门顺流向的振动不会引起过流开度脉动，但在闸门淹没出流时，闸门底缘涡旋的泄放与闸门振动关系非常敏感，两者相互作用后将形成顺流向振动。Thang[7]等人认为该种闸门振动是下游漩涡共振引起的，初始漩涡向下游运动耦合成大尺度的漩涡反馈给闸门。Jongeling[8]对此提出了不同解释，认为下游次生漩涡不会给振动闸门输运能量，闸门振动是由底缘自由剪切层的不稳定使底部压力变化引起的。林勤华[9]、Thang[10]都阐明了闸门顺流向振动是不稳定激励和运动激励共同作用的结果，剪切层分离重附初始的不稳定激振会引起流体共振和流固耦合型的激励，还从漩涡形成的发展规律、压力波分布和向下游传播方式来说明垂向和顺向振动发生在不同折算流速的原因。笔者认为闸门振动是与闸孔出流的漩涡脱落及剪切层的重附着联系在一起的。董淑芳[11]认为闸门振动主要是由水跃表层大尺度漩涡，即表层旋滚，上下摆动往复撞击闸门，从而诱发闸门共振引起的。

12.1.3.2 平底闸门稳态自激响应的条件

笔者在一玻璃水槽中研究了平板平底闸门稳态自激响应，对其动力过程给予了定性分析，阐明了引起闸门稳态自激响应的必要条件。闸门底缘的水流运动可用图12.6来描述。水流自a点开始分离，自由剪切层形成的漩涡在闸门底缘形成压力扰动。随着漩涡的向下游移动和新的漩涡不断产生，就在闸门底缘产生了周期的压力变化，当折算流速V r＜2.0时，闸门的振动响应为随机性的。这可以从三个方面来解释。

（1）此时的折算流速较小，漩涡脱落的频率低，即作用在闸门底缘交变压力的频率低，漩涡脱落的频率可由下面的关系得出：

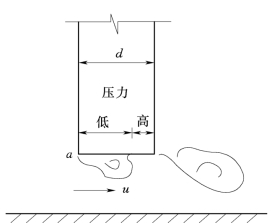
图12.6　平底闸门底缘水流的流动图像(www.xing528.com)

式中：u为闸底平均流速；d为闸门的顺流向厚度；S为闸门底缘漩涡脱落的Strouhal数；f 0为漩涡脱落频率。

Thang等人的研究结果S=0.42。由式（12.29）、式（12.30）可得：

式中：f n为闸门的自振频率。将闸门作为考察对象，只有当强迫力的频率与自振频率接近时，才会产生共振。按式（12.31），闸门产生共振的条件是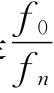≈1，以S=0.42计算，显然当V r＜2.0时，f 0与f n的差值较大，故闸门不会产生稳态共振响应。

（2）受来流紊流度的影响，在沿闸门宽度方向上各点的漩涡脱落相位不一致。如果考察各点脉动压力的互相关，则相关系数会很小。更进一步说，沿闸门宽度方向上底缘各点的脉动压力不同步，也难以激起闸门的共振响应。

（3）折算流速小，意味着底缘平均流速小，作用于底缘的脉动压力强度也小。换句话说，由水流传给闸门的能量小，不足以克服系统的弹性力和阻尼力而激起闸门振动。在实验中发现，当闸门底缘宽2cm时，自振频率f n=0.97Hz，在V r=1.5～0.86和相对开度e/d=0.5～1.0的范围内，没有共振发生。分析认为是底缘窄，脉动荷载作用面小，总的荷载小，激不起门体的振动。当底缘宽度由2cm变为3cm时，其他条件都不变，也未观测到共振响应，可能的原因是自振频率偏低，当漩涡脱落的频率与其相适应时，要求折算流速相对较低，荷载小，也不能激起共振。在此基础上只将自振频率调整到f n=11.57 Hz，即产生了强烈的稳态共振响应。

由此可以说，上面所述的漩涡脱落频率、脉动荷载的相关程度、荷载强度是闸门产生共振响应的必要条件，当V r=2.0～3.0时，上面第一条及第三条得到满足。同时，一旦闸门起振，则对尾流有很强的调整作用。沿闸门宽度方向的漩涡脱落相关作用增强，近乎于二维薄片那样一张一张地被泻落下来，尾流也相当于二维流动。这种相关作用可以从图12.7中明显地看出。此关系图是表示刚性圆柱体处于漩涡脱落共振时沿跨距方向的相关作用，闸门底缘的漩涡脱落与此有相同的机理。这样，由漩涡脱落与闸门振动的连锁效应使得沿底缘宽度方向的周期压力脉动同步，激起了闸门垂直方向的初始共振。几乎与此同时，另一种激励机制也产生了，这就是由振动引起闸下过水有效面积的改变形成流量变化。由于流体的惯性作用，造成了作用于底缘上流体动力学的压力变化。这种作用可由图12.8来描述。当闸门向上运动，在上游的水中存在着惯性的作用，使得单位时间内闸底泄流量增加，即∂Q/∂t＞0引起上游水压力下降，下游水压力上升。这种闸门前后水头差的下降就造成了闸门底缘下吸力的减小，当闸门向下运动，闸下泄量减小，即∂Q/∂t＜0，闸门上下游水头差增大。流体惯性机制加入后，与水流不稳定机制相互影响，直至达到新的平衡。因此闸门最终的稳态响应是底缘水流不稳定的分离和重附着及流体惯性共同作用的结果。当闸门底缘形状不是平底或其尺度与相对开度的组合破坏了重附着的条件，漩涡脱落形成的激励力不存在或者很小，但流体惯性作用依然存在。

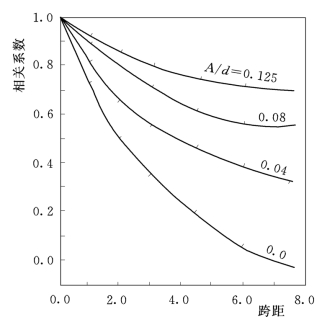
图12.7　平底闸门漩涡共振时尾流沿跨距的相关系数

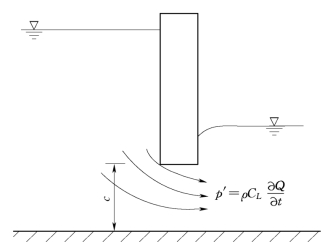
图12.8　平底闸门闸下流体的惯性作用

当V r＞3.0时，至少破坏了前述第一个必要条件，故也不能激起闸门的共振。