流固耦合振动理论的分析方法

该方法的关键是求解闸门振动引起水压力波动（水流运动一般假定为势流），即通过耦联求解方法求出方程式（12.2）的m′、c′和k′，由c′来判定闸门的稳定性。谢省宗[1-2]。用该方法分析了平面闸门平移（顺流向）和旋转振型的振动稳定性特征，给出了定性结果。谢省宗以刘家峡左岸泄水道进口高水头平面工作门在运行中出现强烈振动为实例，从水弹性理论角度进行了闸门振动稳定性分析，认为闸门的振动原因主要是上游胸墙-门体-止水耦合形成的水弹性振动系统，在止水漏水作用下，系统发生水力瞬变过程。考虑闸门的振动和水力瞬变的相互影响，可概化成如图12.1所示的闸门振动和水力瞬变耦合的水弹性振动系统，其运动方程如下。

1.闸门振动方程

2.水力瞬变方程

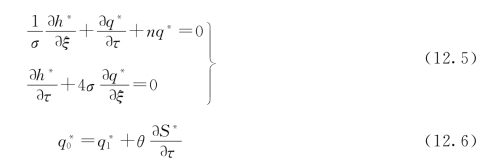
式中：S*、h*（H*）、q*、ξ、τ分别为闸门振动位移、水动力水头、流量、距离以及时间的无量纲量。

对式（12.4）、式（12.5）和式（12.6）作时间τ的拉普拉斯变换，并求解这些方程，以q*为系统的扰动量，以S*或h*（H*）作为系统的输出量，则图12.1构成的水弹性系统各环节可由如图12.2所示数学框图表示。

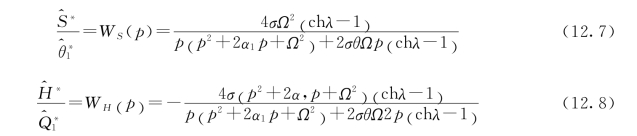
图12.2　闸门-空腔的水弹性耦合振动系统

若在闸门闭合瞬间，顶止水突然闭合，则输入的扰动函数Q^*1为负单位阶跃函数，这时动水压力H*和闸门振动S*的瞬变过程可通过W S（p）、W H（p）逆变换而求得，令（p=jω，分实部、虚部）：

对式（12.10）进行积分，得出原型观测条件闸门闭合瞬间的动水压力瞬变过程线如图12.3（a）所示。由图中可见，压力的第一个峰值、周期以及上支衰减曲线的形状和观测结果相近。

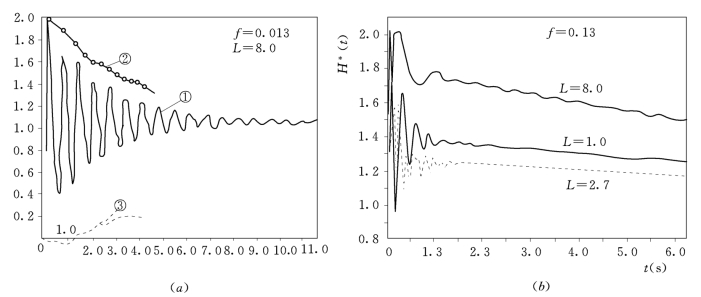
图12.3　改变空腔长度和摩阻水力瞬变过程线的比较

（a）水力瞬变过程曲线（原型比较）；（b）改变空腔长度和摩阻水力瞬变过程线

根据上述水弹性理论，对解决类似刘家峡高压平面闸门强烈振动措施可包括：①在闸门面板上除原来的止水外增加若干横向止水，以增加水力摩阻和减小空腔长度，不同空腔长度的动水压力瞬变过程曲线如图12.3（b）所示；②对闸门主梁的翼缘及腹板进行适当加固。

对于低水头平面闸门振动系统，如图12.4所示，将闸门概化为m个弹性支撑的刚性板的振动包括平移振动S=A eλt及旋转振动φ（t=B eλt），在振动过程中闸门和库水产生耦合动水压力为p（y，t）=p（y）eλt。其中S（t）、φ（t）应满足运动方程组：

式中：M′、J、I′为流固耦合产生的附加惯性项；C1、C 2、C3、C4为附加阻尼项；K 1、K 2为附加弹性项。

(www.xing528.com)

图12.4　平面闸门的振动系统

方程组（12.14）中，A、B前面系数组成的行列式为零的条件，得到频率方程：

观察由式（12.16）表示的频率方程，这是一个待定复数频率λ的四次方程式，其中各项系数中包括了a、H、U、y 0、yi等参数。当各参数取特定值时，将会使频率方程具有正实数根或带有正实数的复数根的解。在这种情况下，微小的振动就成为不稳定的了。在水弹性力学中，具有正实数根的解相应于非周期解，变位按eδt（δ＞0）随时间增加，称为“扩大”；具有正实数的复数根的解相应于周期解，振幅按e（δ+iω）t（δ＞0）随时间增加，称为“颤振”。使不稳定振动开始发生的a、H、U、y 0、yi等参数组成的综合关系式称为“临界条件”。闸门仅有旋转振动的情形下，频率方程给出如式（12.17），即

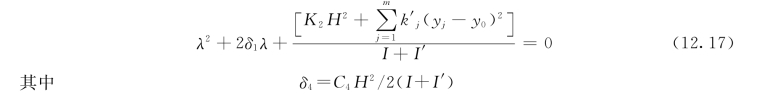
在振动稳定的情形，其必要和充分的条件是必须同时满足：

由第一个稳定条件式（12.17），要求C4＞0，即

若式（12.20）不被满足，则振动系统相当于所谓“负阻尼”的情形（暂不考虑实际阻尼的影响），这时体系的振动是不稳定的。因此，由第一个稳定条件出发，对临界条件可以这样定义：当相对开度为一定时，“附加阻尼”C 4开始出现负值时的相对质心高度称为“临界质心高度”ηOKP，它满足式（12.21）：

式中：k称为平均弹性常数。

因此，由第二个稳定条件出发，临界条件可以有两种定义：

（1）当闸门的结构特性一定，在e等于常数时，开始出现不稳定振动的流速称为“临界流速”U KP，它由式（12.23）决定：

（2）当闸门的结构特性一定，在U等于常数时，闸门开始出现不稳定振动的开度称为“临界开度”e KP，它由式（12.24）决定：

由上述对振动稳定性的讨论中，说明当闸门的结构特性和水力特性各因素组合不当时，轻型闸门发生“颤振”的实际可能性是存在的，因而应该引起闸门设计者的注意。闸门“颤振”现象是应该绝对避免的，因此避免“颤振”的方法具有重要的实际意义。主要措施有：①闸门结构的重量和刚度的合理分布，闸门重心位置过低是不相宜的，而在闸门实际运用中，亦常以加大开度来改变重心位置以避开发生强烈振动区；②改变流动条件以避免“颤振”。如在上游面板加以某种形式的导流坎和隔板，以达到有利的流速分布，也可以避免或克服“颤振”。

此外，Ishii对大跨度斜平面闸门在小开度时振动稳定进行了理论分析，研究表明，该类闸门振动稳定性主要与佛氏数F、闸门倾斜因子K及闸门底缘淹没水深比β*=d r/d 0有关。

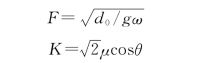
式中：ω为闸门振动圆频率；d r为上游水深；d 0为闸门底缘水深；θ为闸门与底板夹角；μ为流量系数。

F是影响闸门失稳的最主要因素，当F＞Fc（临界值）时闸门振动失稳。对于具体不同的闸门，临界值Fc（可由计算得到）是不同的。由于以上这些理论采用势流假定，因此不能分析出由漩涡不稳定分离引起闸门不稳定性振动，只适应于分析流体结构共振型的振动稳定性。另外，以上的理论分析是针对简单的振动模态，与闸门实测振动存在差距，对于实际复杂模态的振动稳定的数值预测模型研究需进一步加强。