【摘要】：关于闸门振动的危害程度的判别，Petrikat[33]认为振动的危害程度取决于振幅与频率的综合效应。选择测有振幅的数例闸门[34]，运用两种判别方法判别其危害程度见表11.9。因此对于弧形闸门，除了对振动响应进行控制外，还应考虑弧形闸门的动力稳定性，尽可能是弧形闸门远离其动力不稳定区域。表11.8美国阿肯色河的判别标准图11.58金属结构的危险振动表11.9闸门振动的危害程度
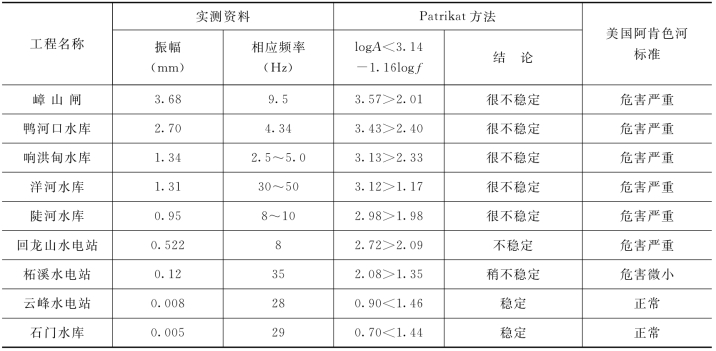
关于闸门振动的危害程度的判别，Petrikat[33]认为振动的危害程度取决于振幅与频率的综合效应。它在对数坐标上将危害程度划分为稳定、合理稳定、可以采用、稍不稳定、不稳定和很不稳定等6个区域，如图11.58所示。并给出安全临界振幅A（μm）应小于某频率f（Hz）的函数表达式，即：log A＜3.14-1.16log f。美国阿肯色河通航枢纽中采用了以振动构件平均位移划分的判别标准（表11.8）。选择测有振幅的数例闸门[34]，运用两种判别方法判别其危害程度见表11.9。由表11.9可知，两种判别方法基本一致，但是Patrikat方法的适用范围尚有可商榷之处。该法的实质为：频率高则允许振幅小，频率低则允许振幅高，虽然从动力学观点来看，对于正则振型，显然存在振动频率愈高振幅愈小的对应关系，但对于弧形闸门，主要问题是支臂失稳，振动过程中支臂本身加速度产生的惯性力不占主要地位，即关键是振幅和轴向荷载起主要作用，而不是频率和振幅起主要作用。按Patrikat观点，似乎可以得出支臂刚度越小、频率越低则允许振幅越大的结论。因此对于弧形闸门，除了对振动响应进行控制外，还应考虑弧形闸门的动力稳定性，尽可能是弧形闸门远离其动力不稳定区域。
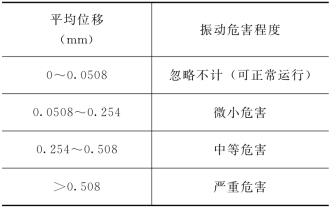
表11.8 美国阿肯色河的判别标准
(www.xing528.com)
图11.58 金属结构的危险振动（允许振幅判别标准）
表11.9 闸门振动的危害程度
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
