如7.4.3所述，由于水流动力荷载及流体—结构相互作用的复杂性，在水弹性模型模拟中存在一些不相似的因素，如阻尼比、泊松比、模拟范围、高频荷载的相似性差等，有必要考虑这些不相似因素的影响对振动响应进行修正。对于水弹性模拟结果的修正，本研究在考虑水流脉动荷载在时间和空间上的随机特性、水流点面脉动荷载的幅值和频率的转换关系、面脉动荷载间的相关关系的基础上，提出用流激振动反分析方法进行修正。首先由实测的动力响应，经反分析求出水流的各类等效荷载，然后针对不相似的因素，修改计算模型的参数。再用正分析的方法求出修正后的动力响应。另外，在模型动力实验中，实测动力响应的测点总是有限的（特别是在原型观测中有时更少），难以全面反映水工结构的动力响应特征，尤其是动应力响应，最大动应力点又常位于水下，难以测量。因此要对水工结构的动力响应进行正确评估，有必要通过实测有限点的响应特征，回归出整个动位移场和动应力场，以便得到最大动力响应值。这也可以通过流激振动反分析方法来实现[9-10]。
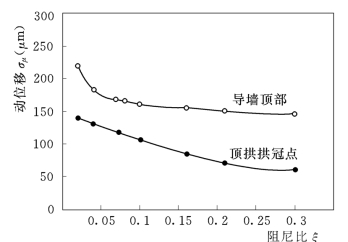
在采用水弹性模型来模拟水流脉动荷载作用下水工结构的动力响应系统时，按模型律的要求，结构模型材料应满足：容重比尺λρ=1。弹性模量比尺λE=λl（λl为几何比尺），阻尼比比尺λζ=1，泊松比比尺λμ=1。其中阻尼比和泊松比相似条件难以满足，其影响应进行适当修正。由于水弹性模型材料采用加重橡胶，其阻尼比和泊松比都偏大，各阶模态阻尼比一般在5%～10%，平均约6.77%，泊松比为0.35～0.40，而实际的水工结构（如东江、泉水双曲拱坝等）的阻尼比为2%左右，混凝土材料的泊松比为0.167。根据实测的动位移响应值和模型的阻尼比和泊松比的实测值，采用以反分析方法求出动力荷载，再根据实际工程结构的阻尼比和泊松比求解动力响应。图10.20、图10.21给出了构皮滩拱坝和三峡导墙结构流激振动的阻尼比和泊松比修正的结果。考虑阻尼比修正后，即阻尼比为2%、7%的动位移响应相比，顶拱拱冠点和导墙顶部的动位移均方根值分别增加了24%和26%；考虑泊松比修正后，顶拱拱冠点和导墙顶部动位移均方根值增加约8%～10%。
(www.xing528.com)
图10.20 构皮滩拱坝激流振动阻尼比对动位移的影响
图10.21 三峡导墙结构激流振动泊松比对动位移的影响
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
