泄流振动响应的谱分析优化方法

在实际工程中，绝大多数的流激振动问题都属于非线性求解问题，但我们可以利用近似的方法使之线性化，从而达到简化问题的目的。对于线性系统，它一般满足下述三点要求：

（1）响应是可以叠加（输入之和的输出等于各个单独输入所得的代数和）而又是齐次的。

（2）系统具有常系数，系统的所有基本性质都不随时间变化。

（3）常系数的线性系统应具有频率保持性，输出与输入的区别只不过是改变了振幅和相位。

对于水流激振问题的研究，其主要取决于两个方面——结构系统和荷载系统，关系式可以表示为：

将结构离散成有限多个自由度，其在随机荷载作用下的运动微分方程为：

式中：[M]为质量矩阵，是结构质量矩阵[M S]和水附加质量矩阵[MW]之和；[K]为结构刚度矩阵；[C]为结构阻尼矩阵；{V¨}、{V·}、{V}分别为加速度、速度、位移矢量；{P}为随机荷载分量。

因一般流激振动问题中均只是以低阶振型为主，若只考虑q个低阶振型，则将式（10.45）分解成q个独立的单自由度系统振动方程：

式中：M j、K j、Cj分别为广义坐标下的广义质量、广义刚度、广义阻尼。上式两边同除以M j有：

式中：ω为结构第j阶振型圆频率；ξj为结构第j阶振型阻尼比；Fj（t）为结构第j阶振型随机荷载作用分量。(www.xing528.com)

由式（10.45）的单自由度振动方程可求得第j阶振型的瞬态反应解：

式中：hj（t）为体系单位脉冲响应函数。

由此任一结点k的位移响应历程为：

由任一结点k位移响应的自相关函数进行傅立叶变换，得到位移响应的功率谱密度：

H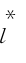（ω）为H j（ω）的共轭复数。对于阻尼较小的体系（在结构工程中一般都是这种情况），振型i所产生的反应与振型j所产生的反应几乎是与统计无关的，同时考虑各点随机荷载相互独立的情况，式（10.51）中互谱密度项和振型交叉项一并消失，有：

则位移响应均方根值为：

当单元中各结点的位移响应向量求出后，可依据式（10.54）求出其应力：

式中：[D]为弹性矩阵；[B]为应变矩阵。