平面水流脉动压力频谱的点面转换关系探析

10.1.2.1 点脉动压力相关特性

1.自相关函数和时间紊动尺度

自相关函数表征脉动压力场中某一点在两个不同时刻t与t+τ的脉动压力之间的依赖关系，其定义为：

表征紊动结构的时间紊动尺度或称时间积分尺度，反映紊流大涡旋的平均尺度，可由自相关函数求出：

式中：τ0为自相关函数第一个使R（τ）为零的τ值；D′P为脉动压力方差值。

表10.1是根据实验数据计算出的脉动压力时间积分尺度L t和时间微分尺度λt，表征脉动压力迅速变化的尺度λt为[3]：

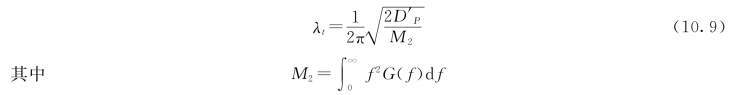
式中：M 2为二阶谱矩；G（f）为谱密度函数。由表10.1知：来流量和下游水垫深度相同，沿射流沿程各区Lt与λt的值都无大的变化，Lt在远离滞点的上、下游射流影响区较在滞点处略有增大的趋势；且Lt随下游水深增大而增大，与时均流场的关系密切，这是因为大尺度涡旋从时均流获取能量的缘故。故时间积分尺度Lt与时均流参数的关系绘于图10.2，可知对于同一测点，U 0 Lt/h约为常数，即：

表10.1　时间积分尺度Lt和微分尺度λt

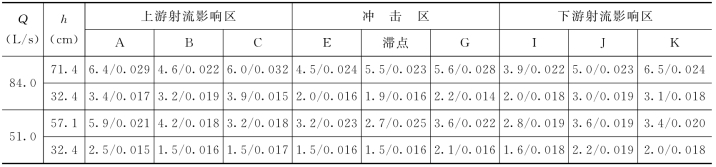
图10.2　时间积分尺度Lt与时均流参数的关系

2.时空相关特征

时空相关函数表征不同空间点在不同时刻脉动压力间的互相依赖关系，反映大尺度相干涡旋在一定空间范围内保持其尺度随时均流向下游传播，时空相关函数表示为：

式中：ξ、η分别为顺水流方向（纵向）和垂直水流方向（横向）的空间距离。显然，当ξ=η=0时，上式就是自相关系数，ρ（ξ，η，τ）与空间点距离和方向均有关，为此先将ρ（ξ，η，τ）分解为纵向和横向时空相关系数，然后将两者再综合起来分析其变化规律。当ξ≠0，η=0时，式（10.11）成为纵向相关函数ρx（ξ，τ）；当ξ=0，η≠0时，式（10.11）成为横向相关函数ρy（η，τ），部分纵向、横向时空相关函数的测算结果示例于图10.3。

由图10.3知，大尺度相关涡旋在滞点上游区向上游传播，在滞点下游区向下游区传播，即在时空相关图上，出现明显的峰值，随下游水深的增大，ρx（ξ，τ）也增大，峰值更明显，且随两点间的距离ξ增大，峰值减小，这表示涡旋在传递过程中的变形和解体，而ρy（η，τ）以τ=0时为最大外，就不再出现较大峰值，这表明横向涡旋传播不明显，主要是横向流速极小，水流涡旋几乎不存在相应的传递通道。

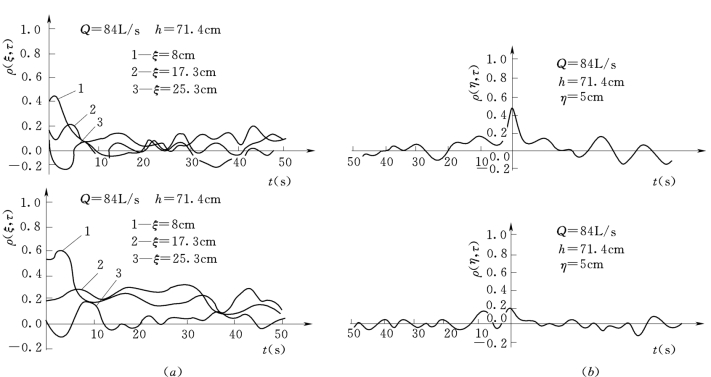
图10.3　时空相关图（ξ为负值，表示向滞点上游传播）

（a）纵向；（b）横向

3.空间相关特性与空间积分尺度

实验结果表明，脉动压力纵、横向的空间相关系数主要受下游水深（或射流扩散程度）的影响，受其他水流参数的影响较小，二维空间相关系数可近似按纵、横空间相关系数的乘积求得，表征涡旋特征尺度大小的纵向、横向空间积分尺度有：

4.泰勒冻结假定

由泰勒冻结假定，空间相关函数（纵向）和时间相关函数转换关系为：

式中：V e为涡旋传递速度，在脉动压力相关分析中：

τm为时空相关图中峰值的时滞，由于ρx（ξ，τm）的值总小于1，说明在传递过程中，涡旋结构将发生变化，并非刚性传递，且不同尺度涡旋的传递速度存在差别，因而，由式（10.15）求得V e只反映脉动压力主要脉动源——大尺度相干涡旋的传递速度，表10.2中给出了滞点下游侧V e的部分实验结果。

表10.2　涡旋传递速度Ve

(www.xing528.com)

由表10.2知，滞点向下游的涡旋传递速度V e为：

利用式（10.10）中U 0 L t/h≈0.41的结果，则

式（10.12）、式（10.17）的结果相近，说明在二元淹没射流中泰勒假定是近似成立的，即纵向空间相关和时间相关可互换。

10.1.2.2 点脉动压力的频谱特性

表征频谱特征的谱密度函数与自相关函数互为Fourier变换，反映了脉动压力的能量在频域上的分布，若用无量纲谱密度GK（f）表示，则有：

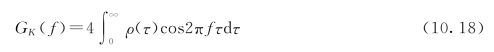
以滞点的GK（f）的测试结果为例示于图10.4。

由实验结果知，各测点谱密度函数值随下游水深而变化，下游水深较小，脉动压力能量在频域上分布较广，随下游水深增大，能量向低频移动，在冲击区内，各测点谱密度函数在水流条件同一的情况下相差不大，这与自相关函数或时间积分尺度的结果一致，将冲击区的谱密度函数进行概化处理，拟合出射流作用下脉动壁压的频谱表达式：

式中：St为斯特鲁哈数。

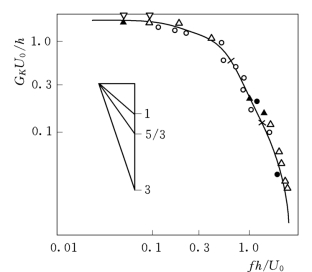
图10.4　冲击区谱密度函数

图10.5　点、面脉动压力谱图

在频谱图（图10.4）上，依次出现频率密度按频率-1、-5/3、-3次幂的规律变化，这是紊流能级的反映，分别对应于紊流能量谱的载能区、惯性区和黏性区，载能区和惯性区交界处的St为0.5～0.6，St小于0.5～0.6的区域是脉动压力的主要频率范围。

10.1.2.3 面脉动压力的频谱特性

实践表明，点、面脉动压力的谱图存在较大的差异，如图10.5所示。工程中更关心面脉动压力谱，利用相关分析方法可推求二元脉动压力场频谱的点、面转换关系。二元均匀场中面脉动荷载自相关函数与点脉动压力时空相关函数的关系为：

结合泰勒冻结假定，可得：

式中：l、b分别为承压面的长度和宽度；Cp′η为横向点、面脉动压力幅值转换系数，表示如下：

对式（10.21）作Fourier变换，取单边谱，并将单边谱无量纲化，则得：

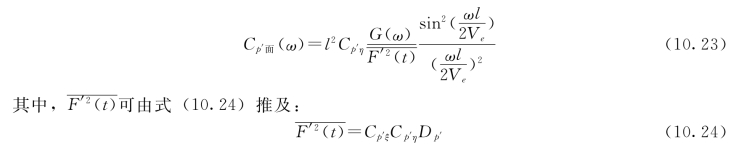
式中：Cp′ξ为纵向点、面脉动压力转换系数。

将式（10.22）、式（10.24）代入式（10.23），得出点、面脉动压力无量纲谱密度函数的转换关系：

式中：GK（f）、Gp′面（f）分别为点、面脉动压力无量纲谱密度函数。

式（10.25）在均匀流内得到，用于非均匀流场，应将上式非均匀流变量（V e、D p′等）用在承压面范围内的平均值代替，由此得二元非均匀场点、面脉动压力的频谱转换关系。

图10.6　管道壁压分析