底流消能导墙动水荷载特性优化

9.2.2.1 时均压强

图9.13为时均压强沿水流方向的分布规律。图中显示在水跃漩滚区，时均压强较小，大约在相对位置x/L j=0.4（L j为自由水跃长度）以后，基本不变，趋于静水压强分布。从图9.14可以看出，导墙上的时均压强沿水深的分布基本上是一条直线，其图形与静水压强相似，呈三角形分布。

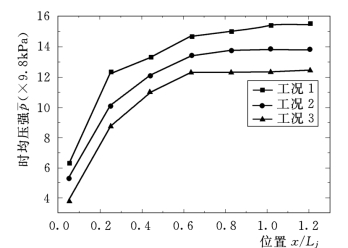
图9.13　时均压强沿水流方向的分布规律

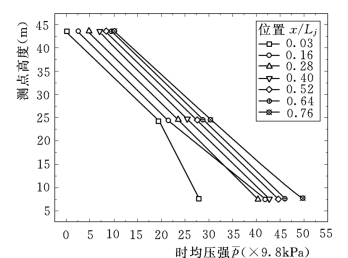
图9.14　时均压强沿水深的分布规律

9.2.2.2 脉动压强

底流消能区导墙上脉动压强沿水流方向的分布是水跃首部为最大，沿程逐渐衰减，整体呈下降趋势，符合一般底流消能脉动压强分布规律；沿水深分布出现底部小上部大的现象，但差别不大。其原因是为了降低水流漩滚对消力池底板的动水压力，在表孔和中孔尾部与消力池底板衔接处设置了高差12m的挑坎，将动水能量导向上部。这一举措虽降低了底板所受的动水压力，却增大了导墙上的动水荷载，而且其合力作用点明显高于静水压力，对导墙的稳定是不利的。脉动压强分布如图9.15所示。从频域角度来看，导墙上的脉动压强是大尺度低频脉动，各工况脉动主频均小于0.25Hz。作用于导墙动水荷载的同步范围较大。

9.2.2.3 整体荷载

作用在导墙上的整体荷载与两侧水流条件有关。如果两侧水流条件相同，理论上时均荷载趋于零，而脉动荷载则占主导地位。若两侧水流条件不同（入池水流弗劳德数不同而形成水位差或一侧为静水），则时均荷载可能达到较大量级，因具体条件而异。

1.荷载沿流向的分布

图9.16为模型实测导墙上的整体荷载沿水流方向的分布（两侧流态基本相同）。从图中可以看出，作用在单个导墙段上的最大整体荷载达到83.58k N/m2，发生在跃首区域的导墙段上。而且，从数据中可以看出，整体荷载时均值与3倍均方差之和大约等于整体荷载最大值，说明符合正态分布。图9.16中显示，处于水跃首部的导墙为受力最危险的区域。从频域角度看，荷载主频不大于0.2Hz，与导墙本身自振频率相差很大，不会引起导墙的低频共振响应。

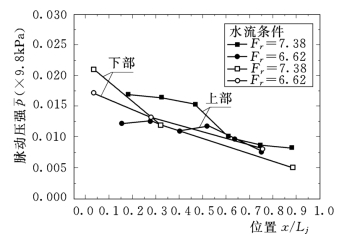
图9.15　脉动压强沿水流方向的分布规律

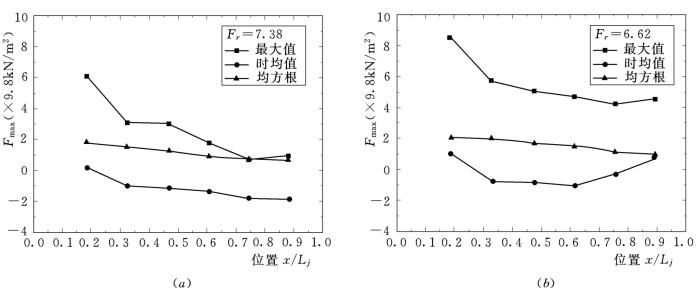
图9.16　典型工况下整体荷载沿水流方向的分布规律

2.脉动荷载与脉动压强的关系

图9.17为脉动压强与脉动荷载的关系，两者大致相等。按底板点面荷载转换方法，令导墙两侧面脉动荷载具有相同的特征，则整体荷载的方差方程为：

令导墙两侧点面脉动压力转换系数为β，并以点脉动压强代入，式（9.8）变成：

可得β=0.71。(www.xing528.com)

3.最大荷载与脉动荷载的关系

图9.18为最大荷载与脉动荷载的关系。两者的关系可以表示如下：

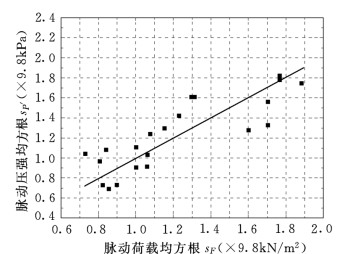
图9.17　脉动压强与脉动荷载的关系

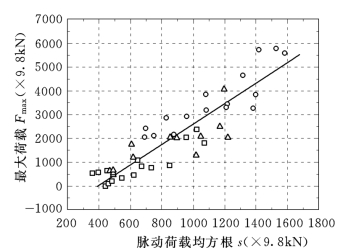
图9.18　最大荷载与脉动荷载的关系

导墙水动力荷载基本是脉动分量，时均量占小部分。这与导墙两侧水流条件有关，若两侧水流条件相同，整体荷载的时均近于零。

4.最大荷载的预测

与消力池底板荷载类似，影响导墙荷载的因素主要是入池弗劳德数Fr、水跃淹没度σj。荷载大小与两侧水流条件有关，下面分述两侧水流条件相同和不同时的模型实测结果和经验拟合关系。

图9.19为两侧水流相同时整体荷载与入池水流条件的经验关系，拟合公式如下：

式（9.11）的试验条件为：q=（140～225）m2/s；Fr=6.62～7.84；σj=0.96～1.29。

图9.20为两侧水流不同时整体荷载与入池水流条件的经验关系，拟合公式如下：

式（9.12）的试验条件为：q=（50～80）m2/s；Fr=10.4～13.6；σj=0.96～1.29。

式中：q为入池单宽流量；H为以消力池底板起算的水头；Fr为入池水流弗劳德数；σj为水跃淹没度；F max为导墙单位面积荷载，一般以跃首处最大。

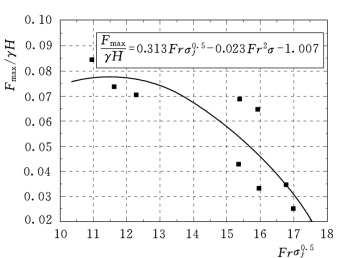
图9.19　两侧水流条件相同的最大荷载

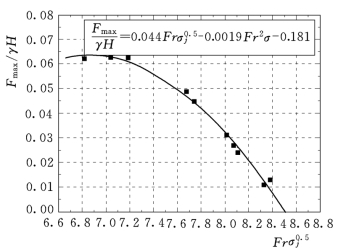
图9.20　两侧水流条件不同的最大荷载