以某弧形闸门为例[9 10],该闸门孔口尺寸为12×16-16m(宽×高-水头),闸门弧面半径24.00m,支铰高度18.00m,闸门为常规止水,其中测水封为L形橡塑水封,底水封为I型橡胶水封,水封座板为不锈钢,启闭杆按缸径500mm,缸体外径580mm,杆径250mm计算,在有限元模型中用梁单元进行模拟。闸门面板梁格以及支臂用三维板壳单元,启闭杆采用三维梁单元模拟,整个结构共分为14358个单元,20844个节点;水体区域沿水流方向取3倍水深作为模拟范围,水体共划分5168个流体单元,6120个节点,有限元模型如图8.20所示。选取闸门相对开度e/h=0.25、0.5、0.75三种典型情况下分别计算闸门空气中(干模态)自振特性以及闸门在水流作用下的流固耦合效应(湿模态),得出以下结论:
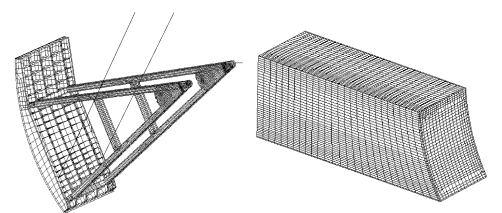
图8.20 弧形闸门及水体有限元模型
(1)闸门系统刚度分布不均匀,抗弯刚度有如下关系:I杆<I支臂<I面板,启闭杆和支臂的一阶自振频率均较低,极易引起振动的部位是启闭杆,其次是支臂,再者为面板。
(2)在闸门开度e/h=0.25、0.5、0.75时,启闭杆的一阶弯曲自振频率分别为1.855 Hz、1.959 Hz、2.261 Hz,振动的部位为油缸下部的起吊杆;从第六阶开始支臂在闸门开度e/h=0.25、0.5、0.75时的振型均是在支臂桁架平面内振动,自振频率分别为5.790 Hz、6.154 Hz、6.630 Hz。
(3)闸门出现了整体的框架振动(第五阶),振动频率为4~5Hz。随着开启程度增大,各阶频率均有所提高,前四阶(启闭杆振动)随着开度增加而增加,主要是由于启闭杆收缩,侧向和轴向刚度增加的原因。(https://www.xing528.com)
(4)在闸门不同开度情况下,受流固耦合影响程度最大的是第五阶模态频率,即两启闭杆轴向拉伸及侧向弯曲振动,闸门整体绕支铰在支臂桁架平面内振动;影响程度次之的是支臂在支臂桁架平面内同相振动。随着闸门开度的不断增加,流固耦合对闸门自振频率的影响程度降低,在闸门开度e/h=0.25、0.5、0.75时,闸门产生整体振动的第五阶自振频率分别降低17.2%、7.6%、1.5%。
(5)受流固耦合的影响,闸门的模态也发生了变化,闸门相对开度e/h=0.25时,从第六阶开始发生变化;相对开度e/h=0.5时,从第八阶开始发生变化;相对开度e/h=0.75时,由于开启较大,流固耦合影响很小,振型基本不发生变化。对于远离面板的(水作用处)的杆件(如启闭杆和支臂)流固耦合效应比较小,典型开度下模态频率及模态特征见表8.12。
表8.12 闸门典型开度(e/h=0.25)下的振动干、湿模态频率及模态特征
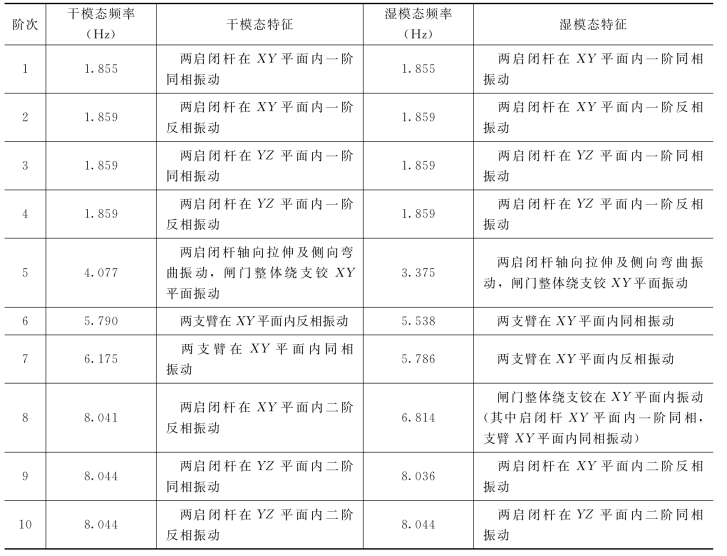
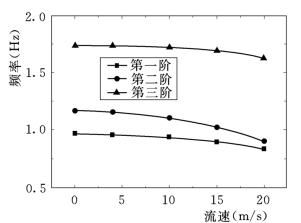
图8.21 流速对闸门自振频率的影响
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




