以某水电站进水口平板工作闸门为例对闸门的模态进行测试与计算分析[8],该闸门靠油压机启闭,孔口宽4.8m,高7.5m,设计水头30.5m,模型比尺采用1∶30。
8.5.1.1 实验模态分析
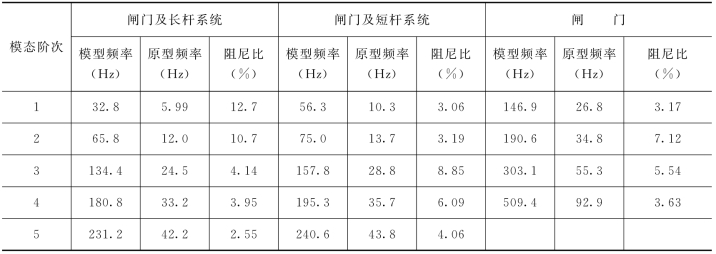
采用8.1.2节所述的结构模态测试分析方法对该闸门进行模态测试,模态响应测点布置如图8.17所示。实测模态频率和阻尼比见表8.9。前四阶振型(闸门板)如图8.18所示。
实验结果表明:
(1)闸门的振动频率是随运行状态变化而变化的。闸门开度小、启闭杆长时,基频低,刚开启时的一阶频率为5.99Hz;随闸门开度的增大,启闭杆变短,基频升高,开度为6m时基频率为10.3Hz;闸门门体自身的频率(底缘受约束)较闸门及启闭杆系统的频率高,闸门门体一阶频率为26.8Hz。
(2)闸门开启运行时,结构体系都是闸门与启闭杆组成的。对于闸门及启闭杆系统,其低阶模态均以启闭杆的振动幅值较大,闸门门体振动幅值较小,主要表现为启闭杆的振动。因此闸门与启闭杆整体的低阶频率的大小主要取决于启闭杆的尺寸。随着振动模态由低阶到高阶,启闭杆依次为一阶、二阶和高阶的杆弯曲模态。
(3)闸门门体的一阶模态主要是绕Z(垂直)轴弯曲振动,振动模态是由低阶的弯曲振动逐步过渡到高阶的扭曲振动。
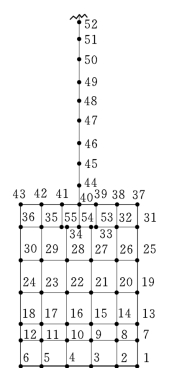
图8.17 模态响应测点布置
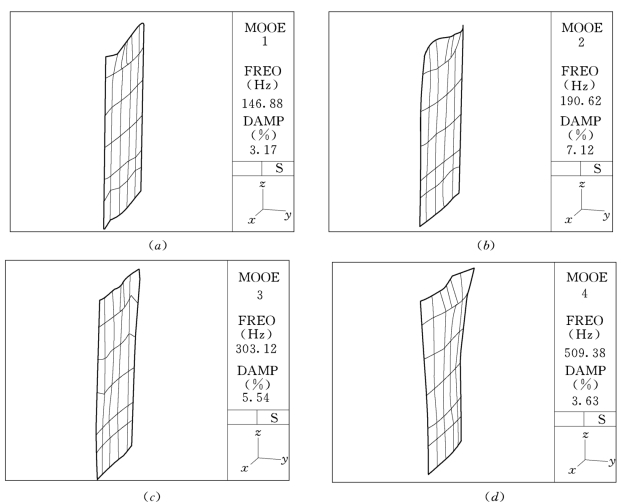
图8.18 闸门板前四阶振型图
(a)闸门模型一阶模态振型图;(b)闸门模型二阶模态振型图;(c)闸门模型三阶模态振型图;(d)闸门模型四阶模态振型图;
表8.9 实测模态频率和阻尼比(https://www.xing528.com)
8.5.1.2 平板闸门结构的模态计算
采用Super SAP程序对闸门系统模态特征进行有限元计算。将闸门结构按板单元剖分,单元总数1148个,节点总数1032个,在主轮处加顺水流方向的约束,在侧轮处加测向约束。计算所得闸门与启闭杆系统前四阶振型如图8.19所示。
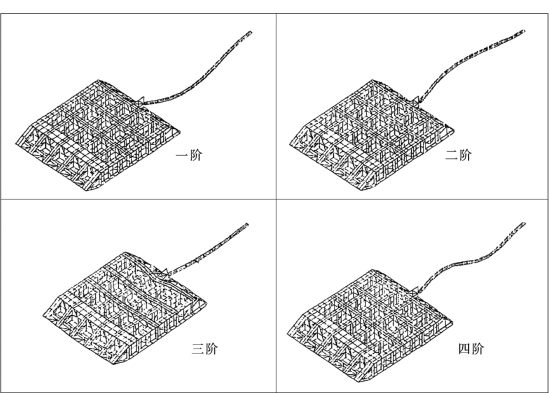
图8.19 典型的闸门与启闭杆系统振型图
8.5.1.3 自振频率的有限元计算与实测值比较
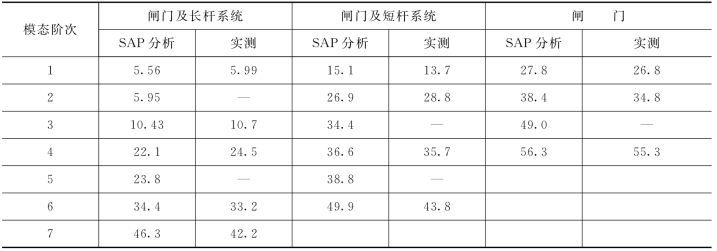
表8.10中的有限元计算与实测的对应频率是按相同振型给出的。可见,两者还是比较吻合的。根据模态有限元计算和实测结果,可以得出以下结论:闸门的振动频率是随运行状态变化而变化的,对于闸门和启闭杆系统,主要表现在启闭杆的振动,闸门门体的一阶模态主要是绕Z(垂直)轴的弯曲振动,闸门与启闭杆整体低阶频率的大小主要取决于启闭杆的尺寸。
表8.10 有限元计算与实测比较单位:Hz
8.5.1.4 闸门干、湿模态的比较
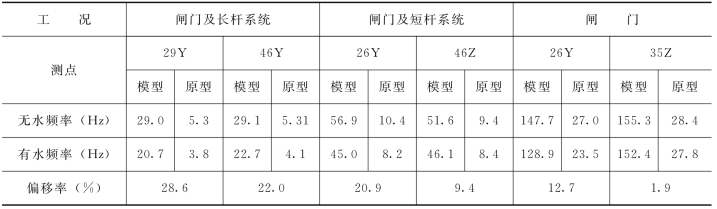
实验和有限元计算都是针对闸门在空气进行,为干模态。在水中的闸门,由于水流与闸门的耦联作用会使闸门模态发生变化。在静水中体具有“附加质量”效应,使闸门结构的频率变低,在动水中水体不但具有“附加质量”效应,而且还具有“附加刚度”和“附加阻尼”效应。“附加质量”效应主要是使闸门自振模态发生变化,而“附加刚度”和“附加阻尼”效应主要是影响闸门的动力响应和稳定性特征。这里仅考虑闸门模态特征的变化。表8.11给出干、湿模态频率的比较。可见有水情况,频率明显降低,测得最大基频下降率可达28%。
表8.11 干、湿模态频率的比较
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




