5.2.1.1 水动力荷载分析
当止水完好时,板块与地基固结良好,锚固钢筋基本不受力,对板块振动有影响的力只有板块上表面由大尺度紊流压力脉动引起的脉动荷载(这时扬压力通常很小,可以忽略),即图5.1(a)中F上的脉动部分。
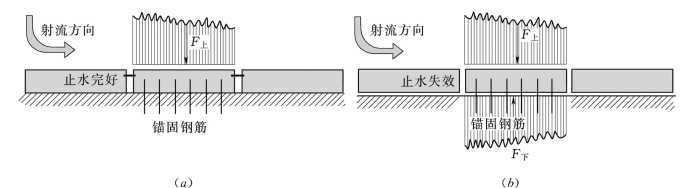
图5.1 水垫塘底板块—锚固钢筋—基岩—水动力荷载耦合系统示意图
(a)止水完好;(b)止水失效
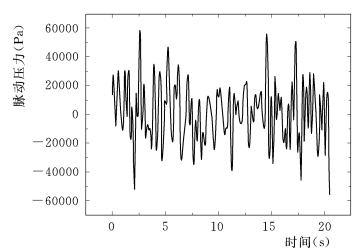
图5.2 典型水垫塘底板的脉动上举力时程线
止水失效后,脉动压力沿缝隙传播。板块除受到锚固钢筋的拉力作用外,还受到强大的脉动上举力,即F=F下-F上[图5.1(b)]的脉动部分引起底板块振动。图5.2为模型实验测得板块的典型脉动上举力。
5.2.1.2 锚固钢筋模拟方法
锚固钢筋的受力过程是一个非常复杂的过程,任何模拟方法都是近似的并有其局限性,至今还没有完全解决。目前,锚固钢筋的有限元计算模型可以采用线单元、实体单元、薄膜单元等型式,钢筋与混凝土(基岩)的连接有固结、连接弹簧单元、接触等常用的方式。
水垫塘防护结构在水流荷载作用下破坏过程呈现出多阶段性,钢筋与基岩和水垫塘底板的相互作用形式也在发生着变化。根据水垫塘底板破坏各阶段的物理特征,在不同阶段采用不同的锚固钢筋模拟形式。钢筋未发生滑移或者滑移较小可采用实体有限元模型、固结连接。钢筋发生较大滑移,必须考虑钢筋与混凝土间的滑移关系。这时可采用2节点线单元模拟锚固钢筋、三向弹簧连接单元模拟锚固钢筋与混凝土(基岩)的连接。线单元计算模型钢筋只承受轴向力作用,即
![]()
式中:Ns为钢筋的轴向力;As为钢筋断面积;σs为钢筋应力。
轴向钢筋与混凝土的黏结应力与滑移量之间的关系应通过试验求出,Nilson采用了Bresler和Bertero对实验资料分析所得的局部黏结应力—局部滑移公式[12-13],即局部τ—s非线性关系表达式:
![]()
式中:τ为黏结应力,MPa;Δ为滑移量,cm。
法向弹簧元刚度取一极大值。
5.2.1.3 水体附加质量
高拱坝泄洪引起底板振动属于流固耦合问题。当水体假定为不可压缩流体时,可以用附加于底板上的附加质量代替,即认为加速度所产生水体的附加质量的惯性力等效于动水压力,到目前为止,还未见到强紊流区附加质量的计算方法,也可采用在静水中确定附加质量的方法。(https://www.xing528.com)
对于平面有限尺寸的板(L×B),附加质量的经验公式[14]为:
![]()
其中
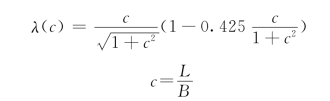
式中:ρ为水密度,考虑水体的附加质量相当于底板的容重增大。
5.2.1.4 接触处理方法
法向接触条件包括不可贯入性条件和法向接触力条件。不可贯入性条件,是指物体A和物体B的位形VA和VB在运动的过程中不允许相互贯穿(侵入或覆盖),接触时以接触力为压力控制条件。切向接触条件为允许发生相对滑移变形。板块间摩擦系数为0.5,板块与基岩间摩擦系数为0.55。
5.2.1.5 非线性时程分析方法
由于止水破坏后,必须考虑板块与地基的接触、锚固钢筋与板块和地基的耦合作用,水垫塘防护结构成为典型的非线性系统,本文采用非线性时程分析法求解。常见的数值解法有中心差分法、线性加速度法、Newmark—β、Wilson—θ法和Houbolt法等。采用Newmark—β法进行求解,具体理论见3.4.1节。
5.2.1.6 水垫塘防护结构模型
目前,国内外对许多水垫塘底部衬砌块断裂、解体后失稳破坏的试验研究证明,水垫塘混凝土底板块最先失稳的位置在射流水舌冲击点下游。因此,本例选择模拟了水垫塘防护结构表孔水舌冲击区末端到中孔冲击区前端的3个端面进行模拟(图5.3),基本涵盖了表孔单独、表中联合泄洪的区域。底板尺寸为9m×9m×5m,边坡护坦板厚3m,护坡模拟到高程1007m处。基岩顺河向长27m,垂直河向117m,厚15m。由原型观测[15]可知A3、B3、C3振动位移较大,因此设定这三块板止水破坏,工况为7个表孔联合泄洪(泄量6300m3/s)。二滩水垫塘底板防护结构有限元模型如图5.4所示。
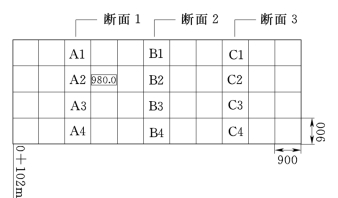
图5.3 计算断面位置示意图
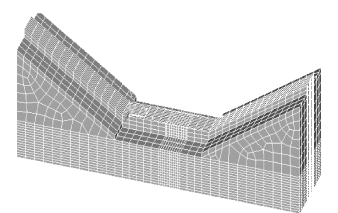
图5.4 二滩水垫塘底板三维有限元模型
当底板止水破坏,钢筋屈服,底板必定发生失稳破坏。因此根据水垫塘底板的动力失稳过程,将止水破坏、锚固钢筋屈服前的动位移响应过程分为3个等级,相应建立3个有限元模型。模型1底板止水完好、钢筋与底板和地基胶结良好;模型2底板止水破坏,不考虑钢筋的滑移作用(底板、钢筋和地基交会的节点为同一个节点);模型3底板止水破坏,考虑锚固钢筋的滑移作用。各种材料参数见表5.1。
表5.1 材料参数

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




