反拱底板局部稳定抗力优化研究

为了有效地防止底板的局部破坏，通常需要确定反拱底板局部稳定抗力。通过考查板块在不同荷载下的位移变形规律，可分析出当变形（位移）速率突然增大时，往往就是反拱形结构发生局部破坏的时候。因此，取板块位移增长率突然增大的那一点作为底板块的极限抗力点，从而得到板块保持稳定的极限抗力。

对所研究的板块施加均布载荷，采用静力分步加载模式，静力分析中的时间为伪时间，是虚构的，无实际意义。在不同荷载下，板块有不同的位移，对荷载—位移曲线离散求导就可得到板块在某一荷载处的位移变化率，板块临近失稳时，板块的位移变化率通常会出现变化（突然增大），以此来判断板块的临界状态。出现变化的那一点，本书称之为“拐点”，如图3.21所示，可以认为拐点处的荷载即为板块能维持稳定的极限荷载，因为拐点过后，板块的位移增长率明显变大，板块很快破坏，图3.22为反拱形板块的失稳形态。

分析中发现，边缘板块的位移变化曲线由两部分构成，即平滑段和上升段。拐点为平滑段的末端，也就是上升段的始端，当荷载超过拐点处的荷载时，板块位移增长率迅速变大，继而失稳。内部板块的位移变化曲线与边缘板块不同，它也由两部分构成，即平滑段和屈服段，板块处于平滑段时，板块可以通过自身的抗力维持稳定，一旦越过拐点，即平滑段的末端，板块的位移增长率迅速变大，而后又迅速减小，甚至为负值，而后再变大，就这样一直到破坏，所以本文认为拐点为板块能维持稳定的临界点，对应的荷载值即为板块能维持自身稳定的极限抗力。

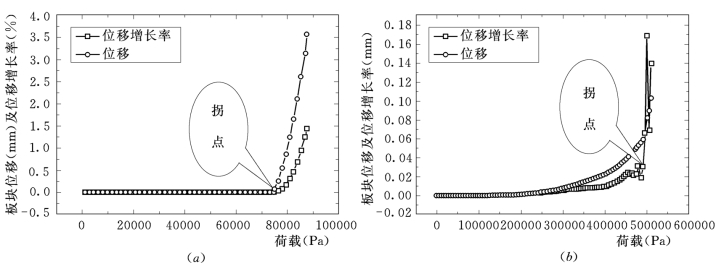
图3.21　位移变化曲线

（a）边缘板块；（b）中间板块

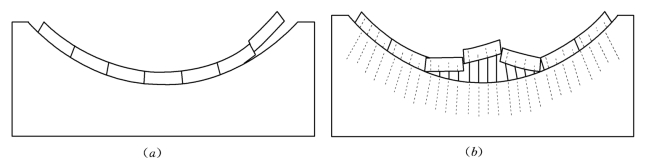
图3.22　反拱板块的失稳形态

（a）边缘板块；（b）中间板块

为了验证反拱底板局部稳定分析的数值模型的可靠性，对某工程实例进行分析，并将计算结果与模型试验的结果进行比较，如图3.23所示，结果表明，数值模型计算结果与模型试验结果吻合良好。说明数值模型在一定程度上能反映板块的实际受力特征，计算结果具有一定的可信度。

图3.23　位移变化曲线(www.xing528.com)

（a）拱端力N=0；（b）拱端力N=1.5G

某工程反拱底板有5个板块，且反拱两侧的底板结构是对称的。因此，取任一侧的3个板块计算结果即可，从边缘板块开始，依次定义为边缘板块、中间板块、中心板块。假定与反拱底板尺寸相当的平底板，以研究反拱底板与平底板之间的区别。以中心板块为例，由图3.24中的位移变形速率曲线可确定出平底板及反拱底板的极限抗力；中间板块有锚固时的局部失稳破坏形态如图3.25所示。

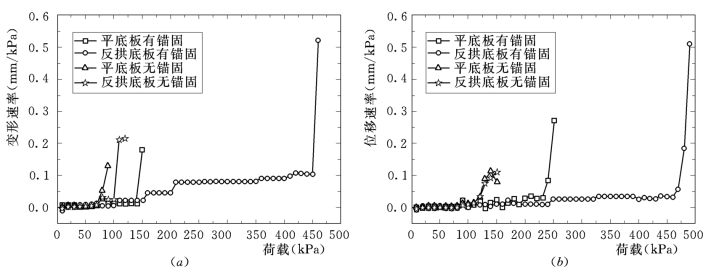
图3.24　中心板块的位移变形速率

（a）无键槽；（b）有键槽

由结果得出：设置键槽及锚固钢筋对于提高底板块的抗力有较显著影响。设置键槽可使反拱底板块的抗力提高5%～20%，使平底板的抗力提高60%～70%，这是由于未设键槽时平底板的抗力由单块板提供，而设置键槽后抗力由该板块与其相邻的板块共同承担所造成的。平底板各板块的抗力基本一样，反拱底板则是中心板块抗力最大，边缘板块抗力最小。图3.26为反拱底板与平底板各板块的抗力比较，由图可知，在设计锚固水平（7.6t/m2）条件下，对于不设键槽的情况，反拱底板的抗力较平底板的抗力提高约1～2倍；对于设置键槽的情况，则反拱底板的抗力较平底板的抗力提高约50%～100%。

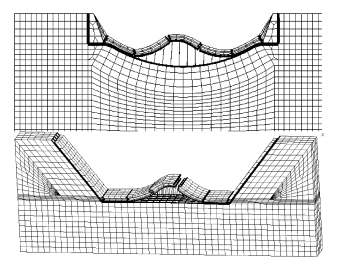
图3.25　中心板块失稳的形式

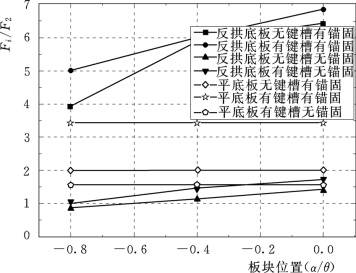
图3.26　反拱底板与平底板的极限抗力比较

注 图中的θ为反拱形底板整个拱圈的圆心角的1/2，α为计算板块的径向与竖直向的夹角