消力塘底板的稳定是实现消能和防冲的关键,其受力和运动过程十分复杂。在水动力荷载的作用下,其响应是水体—防护结构(底板、岸坡)—水动力荷载(渗流力或瞬变力)—锚杆—基岩耦连接构体系动力响应,受力和运动过程十分复杂。反拱形水垫塘与平底水垫塘相比,结构更为复杂,除了处理好水体、底板、荷载、锚杆和地基的关系外,还要处理好各个板块间、板块与拱座间的关系。因此,寻求一种符合反拱形消力塘实际受力状态的力学理论和数值模拟方法非常关键,对它的数值模拟通常需要考虑以下三个方面:锚固钢筋与底板、地基之间的黏结滑移;底板之间、底板与基岩之间、底板与拱座之间的接触以及底板与水体之间的相互作用问题。目前,比较合理的模拟方法为采用三维非线性弹簧单元模拟锚固钢筋与基岩的位移协调、接触元模拟衬砌块接缝以及底板、拱座、基岩和边坡间的碰撞、滑移行为,采用附加质量考虑水体与底板之间的相互作用。
3.2.1.1 非线性的接触理论
接触问题作为工程问题之一,属于典型的状态非线性问题。当两个物体在边界处发生接触时,接触面的大小及接触应力的大小与接触面的初始间隙、摩擦力及荷载的大小有关。在加载过程中,接触面大小不断地改变,即边界条件在不断地变化,使得计算过程相当复杂。
反拱水垫塘板块与基岩、边坡与基岩、板块与拱座、拱座与边坡,以及板块之间都是典型的接触行为,在数值模拟中应按接触处理,才能很好地反映结构的实际受力和运动状态。
1.接触问题的描述
接触问题有两种求解方法,即解析法和数值法。接触问题的解析法又称为经典接触力学,经典接触力学只能求解一些几何形状比较规则的物体,应用范围非常有限。接触问题的数值解法又可以称为非经典接触力学,随着计算机技术的发展,接触问题的数值解法发展迅速,尤其有限元法得到了广泛应用。

图3.3 接触点对
另外,接触问题的状态在初始时难以确定,只有通过接触条件来判断接触物体处于何种接触状态。接触界面条件包括:法向接触条件和切向接触条件。
(1)法向接触条件。法向接触条件判定物体是否进入接触以及已进入接触应该遵守的条件。法向接触条件包括不可贯入性(Impenetrability)条件和法向接触力为压力条件。不可贯入性条件,是指物体A和物体B的位形V A和V B在运动的过程中不允许相互贯穿(侵入或覆盖)。
由图3.3所示,设tx p A为tSc A上任一指定点P在t时刻的坐标,该点至tS c B面上最接近点Q(t x B)的距离tg可表示如下:
![]()
不可贯入性条件要求tg的法向分量tg N满足下式:
![]()
法向接触力为压力要求接触面法向接触力t F N A,t F N B应满足如下条件:
![]()
(2)切向接触条件。切向接触条件是判断已进入接触的两个物体的接触面的具体接触状态,以及它们各自应服从的条件,包含无摩擦模型和有摩擦模型两种。
1)无摩擦模型。如果两个物体的接触面是绝对光滑的,或者相互间的摩擦可以忽略,此时分析可采用无摩擦模型,即认为接触面间的切向摩擦力为零。亦即
![]()
2)有摩擦模型——库仑(Coulomb)摩擦模型。如果接触面间的摩擦必须考虑,则应采用有摩擦的模型,本文采用这种模型。库仑摩擦模型因其简单和适用性而被工程广泛的应用,库仑摩擦模型认为切向接触力t F T的数值不能超过它的极限值μt F N。
当t F T<μt F N时,接触面之间无相对滑动,即接触面间的相对滑动速度tv满足:
![]()
当t F T=μt F N时,接触面之间发生切向相对滑动,这时接触面间的相对滑动速度tv满足:
![]()
2.接触系统的平衡方程
用增量方法求解接触问题时,在时间t+Δt位形内与平衡条件相等效的虚位移原理可以表示为:

其中A、B为两个求解区域,t+ΔtW L是作用于t+Δt时刻位形上外荷载的虚功,t+Δt W I是作用于t+Δt时刻位形上惯性力的虚功,如果惯性力的影响可以忽略,则t+Δt W I=0,问题变成静态接触问题,t+Δt W c是作用于t+Δt时刻接触面上接触力的虚功。
3.2.1.2 黏结滑移的模拟
钢筋与混凝土的黏结是钢筋与外围混凝土之间的一种复杂的相互关系,通过它来传递二者间的应力,协调变形。这是钢筋与混凝土两种材料组成的复合构件共同工作的前提。通常所谓黏结应力是指沿钢筋与混凝土接触面上的剪应力,它使钢筋应力沿钢筋长度而变化。
1.黏结滑移的本构关系
在有限元对钢筋混凝土进行模拟分析时,需要用到黏结应力τ与滑移量S的数学关系。τ—S曲线模型主要有连续曲线模型和分段折线(曲线)模型[25]。
(1)连续曲线模型。用连续的曲线方程来描述黏结—滑移关系,可以得到连续变化的、确切的切线或割线黏结刚度值,在有限元分析中应用比较方便。为简便计算,常将黏结应力τ表达为滑移量s的多项式:
![]()
在实用中通常取前3~4项,并根据试验数据的统计回归分析建立起曲线方程。
如:Nilson、Bresler、Bertero得到的曲线方程为[26-27]:
![]()
式中:τ的单位为MPa;S的单位为mm。
Houde和Mirza在此基础上考虑了混凝土强度f c的影响,得到曲线方程为[28]:
![]()
式中:f c为混凝土抗压强度,单位为MPa;τ的单位为MPa;S的单位为mm。清华大学腾智明[29 30]教授还考虑了保护层厚度c、钢筋直径d和黏结力分布的影响,得到:
![]()
式中:F(x)为黏结力分布函数;τ以MPa为单位;c为保护层厚度;d为钢筋直径;x为至最近裂缝的横向距离,c、d、x均以mm为单位。裂缝间距最大取300mm。
(2)分段折线(曲线)模型。将黏结—滑移曲线简化为多段式折线(曲线),已有多种建议的模型,如3段式、5段式、6段式等。在确定了若干个黏结应力和滑移的特征值后,以折线或简单曲线相连即构成完整的τ—S本构模型。
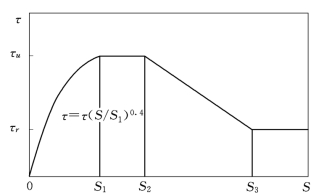
图3.4 CEB-FIP MC90的τ—S模型
表3.1 τ—S曲线的特征值

如模式规范CEB—FIP MC90建议的4段式模型[31]如图3.4所示,参数值见表3.1。徐有邻[32-33]通过试验给出的黏结滑移本构关系的简化模型,简化地采用三段式τ—S关系曲线如图3.4所示,其中3个特征点:cr(τcr,Scr)、u(τu,Su)和r(τr,Sr)的数值由表3.2确定。用式(3.12)、式(3.13)分段定义各曲线段,位置函数用式(3.14)表达,黏结滑移本构模型为两者的乘积。(https://www.xing528.com)
表3.2 基准试件的特征强度和特征滑移量

注 表中混凝土抗拉强度ft=0.267fc2u/3,临界保护层厚度(c/d)cr为4.5,超过此值取4.5计算。

![]()
残余段为经过残余点(τr,Sr)的水平线,即τ=τr (S>Sr)
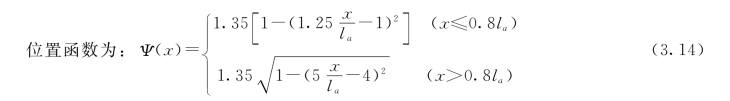
2.锚固钢筋有限元的模拟方法
钢筋与混凝土(基岩)的连接,有以下几种方式:
(1)固结。假定钢筋与混凝土(基岩)之间是完全固结的,没有任何相对变位,钢筋的应变等于它周围混凝土(基岩)的应变。
(2)弹簧连接单元。如图3.5所示,在钢筋与混凝土(基岩)间设置连接单元,把钢筋与混凝土之间的接触力集中在一组弹簧上,钢筋表面与混凝土(基岩)之间的距离为零。设切向弹簧常数为k h,法向弹簧常数为k v,在局部坐标系(H,V)中,节点力与节点变位的关系为:
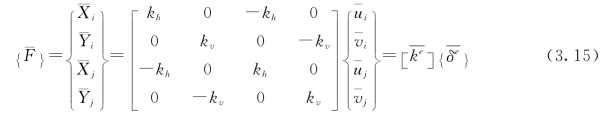
式中:[ke ]为局部坐标系中的刚度矩阵。
进行坐标变换后,得到整体坐标系(x,y)中的弹簧单元刚度矩阵如式(3.16):
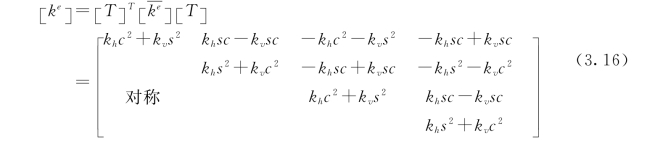
其中
![]()
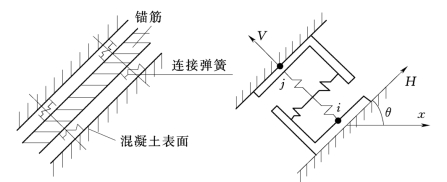
图3.5 弹簧连接单元
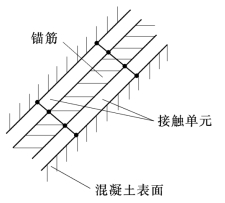
图3.6 接触连接单元
(3)接触单元。在钢筋与混凝土(基岩)之间设置特殊的接触单元,通过接触单元的变形来模拟钢筋和混凝土之间的黏结和滑移现象,如图3.6所示。
3.黏结滑移在ANSYS中的实现
为全面考虑钢筋混凝土之间的相互作用,在ANSYS有限元分析中,可以在钢筋混凝土相对应结点之间采用一组相互垂直的非线性弹簧单元(Combination39单元)来模拟钢筋混凝土之间的黏结—滑移现象,每一个弹簧的性能是由弹簧的力—变形曲线(F—D曲线)确定的。
(1)纵向弹簧(平行于钢筋方向)。该方向为钢筋的埋置长度方向,该方向的连接面上的共同作用即为钢筋与混凝土之间的黏结滑移,因此F—D曲线可以通过黏结—滑移曲线根据以下方法来确定。
首先根据黏结滑移本构关系,确定第i个弹簧对应位置处黏结—滑移对应关系:
![]()
则该弹簧单元的F—D曲线的数学表达式为:
![]()
式中:A为钢筋单元与混凝土单元的连接面面积;d为一根钢筋的直径。
(2)法向弹簧(垂直于钢筋方向)。对于法向弹簧,其弹簧刚度kv取值较复杂,文献[34]介绍:在实际梁中,当裂缝扩展较大时,垂直于纵向钢筋的黏结力与钢筋的暗销作用和梁的向下挤压作用均有很大关系。在此情况下,黏结力不仅与化学性的黏结力和钢筋与混凝土之间的机械咬合力有关,而且还与钢筋四周的混凝土是否能很好握住钢筋有关。实际上是一个三向受力问题。
当裂缝宽度不大,或在裂缝两侧附近有钢箍时,向下挤压作用较小,还不会使混凝土发生水平劈裂,此时钢筋在垂直方向的移动很小,甚至可以忽略不计,可认为混凝土和钢筋在垂直方向是刚接的,于是可假定k v为与混凝土受拉弹性模量成正比的一个很大值。
![]()
式中:E为混凝土受拉弹性模量;bn为梁在钢筋高度处的净宽;b为梁宽;l为连接单元沿钢筋纵向的间距。
以上方法是一种近似的处理方法。文献[35]中建议取一个与混凝土弹性模量同量级的大数,故本算例中kv取值为5×1010。
3.2.1.3 有限元模型的实例
某工程双曲拱坝最大坝高250m,电站装机容量6×700MW,为Ⅰ等大(1)型工程。坝址区为高山峡谷地貌,两岸坡陡峻,高差近700m。坝后主要消能建筑物为水垫塘和二道坝。坝址的地形、地质条件决定了消力塘更适宜采用反拱底板衬砌形式,反拱形消力塘是利用天然河床的形状,将底板做成反拱形,对保护坝基、不刻意开挖、维护坝肩抗力体的完整性都十分有利。反拱水垫塘长度约218.30m,消力塘坝下0+055.4桩号上游体形按梯形断面修改,底板高程2227.0m,下游体形横剖面按圆弧设计,从上游到下游等宽布置,沿水流向14.2m为一段分永久缝。底板最低点高程2214.5m,底板厚度3m、2.5m,反拱中心角61.647°。每个拱圈内将底板分成5块。消力塘与拱坝、二道坝之间设伸缩缝,其施工缝和永久缝均设止水。消力塘底板全断面布设锚筋并设有抽、排水设施。反拱形消力塘横断面如图3.7所示,图中高程以m计,其他数据单位为cm。
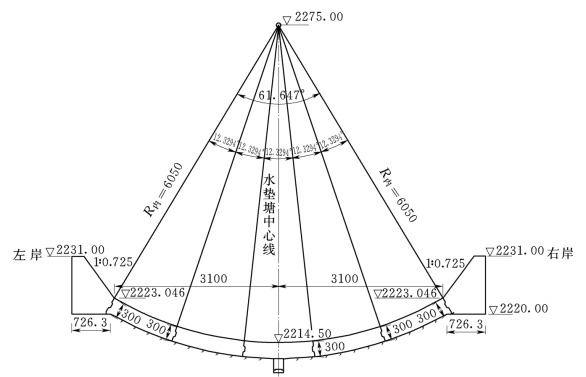
图3.7 某工程反拱形消力塘横断面图
根据以上介绍力学模型建立消力塘反拱底板有限元模型(图3.8),底板沿拱圈方向均匀分成5块,边缘底板与拱座相连,板块、拱座、边坡、地基相互之间均采用非线性接触处理。板块、拱座为混凝土材料,采用Solid65单元来模拟,混凝土材料间的滑动摩擦系数0.5,基岩材料为花岗岩,采用Solid45单元,混凝土材料与花岗岩间的摩擦系数为0.55。锚筋垂直于接触面均匀布置于反拱底板上,如图3.8(c)所示,底板和拱座锚固水平为7.6 t/m2,边坡锚固水平为5.0 t/m2。锚筋与混凝土相对应节点之间采用Combination39单元模拟黏结滑移作用。有限元模型中各材料属性见表3.3,钢筋及混凝土的应力—应变曲线如图3.9、图3.10所示。
表3.3 材料属性

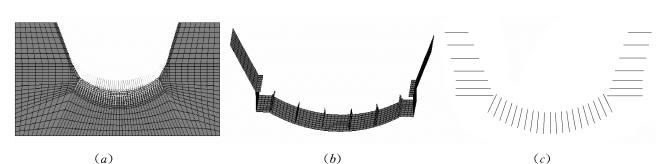
图3.8 有限元模型
(a)整体模型;(b)接触单元;(c)锚固钢筋单元

图3.9 钢材的应力—应变曲线
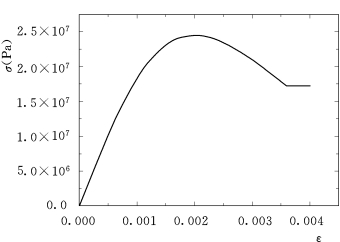
图3.10 混凝土的应力—应变曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




