平底板稳定的控制指标优化技巧

2.3.6.1 挑跌流消力塘底板稳定的控制指标

消力塘作为防护下游河床的结构，其自身在高速水流冲击下的稳定性是实现消能和防冲目的的关键所在。目前，我国工程上采用的底板抗浮稳定的控制指标是冲击压强ΔPm≤150kPa和分布系数α≤1.0。本节结合溪洛渡、拉西瓦、锦屏一级、糯扎渡等工程消力塘模型试验研究，对高坝泄流消能防护结构的稳定性控制指标进行了探讨[47]。

中川博次认为，跌落水舌对河床基岩的冲刷，主要是高速水流进入岩石缝隙，在其底部产生较大动水压力，而表面压力减小，从而形成上下表面压力差，产生上举力，岩层上浮破坏。因此对动水压强ΔPm及分布系数α（最大冲击压强与其作用距离的比值）提出一个限值。对消力塘底板稳定问题，亦参考这个特征值。由日本的凌北等5个拱坝溢流工程，给出时均冲击压强ΔPm均在300k Pa以下，分布系数α在1.0以下的控制指标，这些工程都安全运行。我国设计二滩工程消力塘底板时，采用时均冲击压强标准ΔPm=150k Pa。小湾、构皮滩等水电工程，其消力塘底板冲击压强均控制在150k Pa以下，甚至降至100k Pa。目前在溪洛渡、拉西瓦、锦屏一级等高坝消力塘设计中，仍采用这一标准。即使如此，有些专家对底板的稳定性仍心存疑虑。另外，在消力池底板设计中，采用脉动压强作为控制指标，即底板上的脉动压强均方根不超过入池流速水头的5%～10%。

冲击压强ΔPm及其分布系数α这两个指标有丰富的内涵，应用起来比较简洁、方便。但它的来源纯粹是日本几个工程的统计结果，没有进行即便是简单的水动力学推演。因而在具体应用时，自然会产生诸多疑问。尤其日本凌北等6个拱坝无论是坝高还是泄流流量，都不能与我国正在设计的几座高拱坝相提并论，类比性较差。各个工程的水力条件、地质条件、结构条件不相同，用同一个指标去控制显然有不合理之处。从定性分析角度，最终影响底板稳定的因素是作用在其上下表面的动水压强，导致底板浮升失稳的上举力是上下表面动水压力的合力，包括时均和脉动两部分。显然，上举力与动水压强有正比的关系。在定量方面，ΔPm很难直接与上举力挂钩，从物理概念上，也不好理解。第一，作用在底板上下表面的动水压力与板块面积有关。由于点脉动压强与面脉动压力之间的转换不是简单的倍数关系，不同尺度板块单位面积所能抵抗的动水压强不相同，因此，用一个指标控制显然不合适。第二，板块抵抗水动力荷载的能力与其厚度有关。尽管在强大的动水荷载面前板块厚度产生的抗力显得微不足道（每增加一米可抵抗14k Pa的动水压强），但对其下表面荷载特性的影响还是深远的，主要表现在脉动压强沿缝隙传播方面。第三，板块的稳定性与锚固水平有关。地质条件、施工技术都可能使可能施加的最大锚固力因不同工程而异。第四，冲击水舌的特性更是直接影响冲击压强的大小。对于挑流消力塘，水舌入水角为45°左右，在某些运行工况下，底板上的压强分布甚至不存在典型的尖峰形态。若以下游水深作为起算冲击压强的基准，所有区域的压强都是负值。笔者在进行某高坝溢洪道消力塘水工模型试验中间，发现所有运行工况下底板压强水头都低于下游水位，但模型试验结果却是大部分区域底板处于不稳定状态。另外，对于底流消能的消力池来说，不可能存在ΔPm，但不能就此认为底板是稳定的。

综上所述，认为用ΔPm作为底板稳定的控制指标，应将其与整体荷载（上举力）联系起来，给出明确的量化关系，在力学概念上有所交代。或者寻求另外的参数，例如点脉动压强作为控制指标。

1.脉动压强与冲击压强的关系

已有的研究成果表明，突变流动边界（如水跃、淹没射流等分离流）上，脉动压强主要是由分离或扩散形成的大尺度漩涡所控制。考虑到紊动强度与水舌入水速度有关这一事实，进而知脉动压强与冲击压强直接相关。图2.74是几个工程模型实测脉动压强和冲击压强的结果。可以看出，试验范围内二者之间基本上呈固定的比例关系。

定性上分析，冲击压强随水垫深度的增加而减小。在较小高度冲击射流（ht/d 0≤5）情况下，水舌动能的70%以上可以转化为压能即冲击压强，而大高度射流（ht/d 0＞50）由于水垫的耗能作用，仅有约5%的动能到达底板转化为压能[37]。脉动压强主要是水体紊动能的转化，虽然也随水垫深度的增加而减小，但衰减速度较冲击压强为慢。因此，二者的比值σp′/ΔPm随水垫深度的增加而增大。图2.75几个工程试验的水深ht/d 0约在20左右，大体上有如下关系：

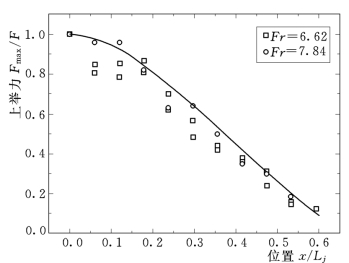
图2.74　最大上举力的沿程分布

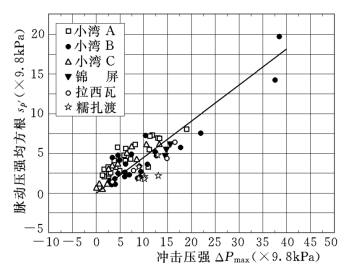
图2.75　实测脉动压强和冲击压强的关系

文献[48]和文献[1]在二元水槽中的试验结果如图2.76所示。图2.76（b）中的d 0是扩散后的水舌厚度，与图2.76（a）有较大的差别，本文的数据与文献[37]协调，结果接近。尽管图中二者的横坐标不协调，但从两图中曲线变化趋势分析，σp′/ΔPm在0.4～0.6之间，再大的数值则对应更大高度冲击射流，与本文的结果没有可比性。另外，图2.76是整体模型三元水流的试验结果，与二元水槽的试验结果可能有一定的差别。因此，式（2.71）基本上能反映消力塘冲击压强与脉动压强的关系。

如果以冲击压强作为控制指标，例如取ΔPm=150kPa，则意味着脉动压强的控制标准为67.5k Pa。

2.脉动压力的点面转换关系

作用在板块上的脉动上举力是板块上下表面脉动压力的合力，可表示为：

式中：F′、F′1、F′2分别为单位面积上板块所受的脉动上举力、上表面动水压力、下表面动水压力的脉动分量。求上式的方差得：

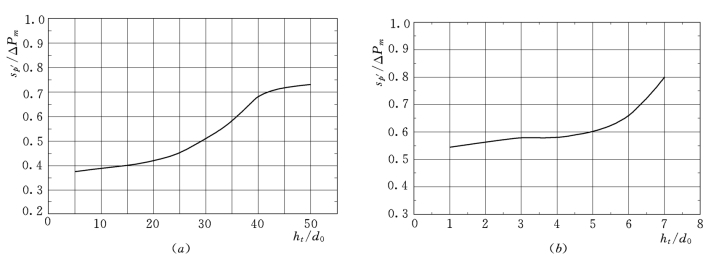
图2.76　冲击压强与脉动压强的关系

（a）为文献[48]试验结果；（b）为文献[1]试验结果

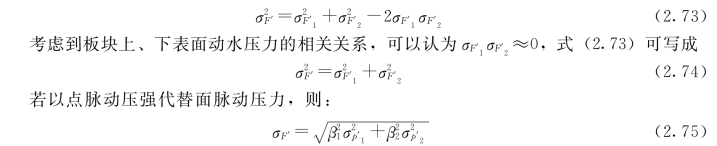
式中：β1、β2分别为上、下表面脉动压强点面转换系数；σp′1、σp′2分别为上、下表面点脉动压强均方根。取β1=β2（考虑到底面脉动压强在缝隙中的传播特性，实际上β1＜β2）。有研究结果表明[49]，上、下表面点脉动压强关系为σp′2=0.7σp′1，则：

式（2.76）即脉动压强与脉动上举力的关系，给定脉动压强点面转换系数，可由此估算脉动上举力。

图2.77给出了三个工程模型实测底板脉动上举力（峰值位置）与脉动压强的关系。从图中可以得到结论：板块单位面积的上举力均方根与脉动压强均方根的关系为：

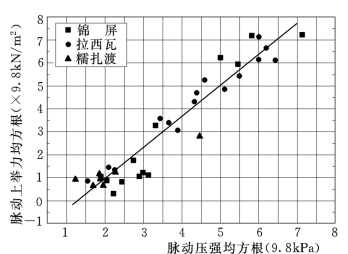
图2.77　脉动压强与脉动上举力的关系

(www.xing528.com)

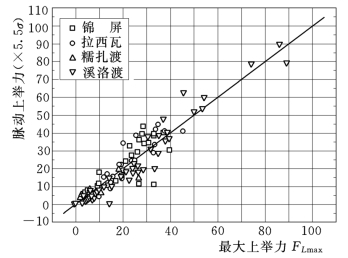
图2.78　脉动上举力与最大上举力的关系

再由式（2.76）可以计算出冲击区脉动压强点面转换系数β=0.38～0.77。实际上这个数值可以理解为上、下表面点面转换系数的平均值，上表面小而下表面则大。

由上面的推演及试验结果，基本上可以得出明确的量化概念：脉动压强与脉动上举力量级相当。

3.底板稳定控制指标的讨论

图2.78是四个工程模型实测最大上举力与脉动上举力的关系，且平均有F max=5.5σF。若评估底板稳定性是用瞬时最大上举力，即考虑在某一瞬时，作用在底板上表面的动水压力最小而下表面动水压力最大，此时上举力达到最大。关于上下表面动水压力的相关性，本书不进行讨论。

综合前面已经得出的公式：

由式（2.78）可进一步得出冲击压强与上举力的关系为：

取式（2.79）的平均值：

式中：F max为瞬时最大上举力，9.8k N/m2；ΔPm为从下游水位起算的冲击压强，9.8kPa。式（2.80）也可表述为：9.8kPa（1米水柱高）的冲击压强相当于18.6k N/m2（1.86t/m2）的上举力。

按目前国内各工程普遍采用的标准：ΔPm≤150k Pa，由式（2.80）即可得出相当于279k N/m2（27.9t/m2）。

由式（2.78）还可得出以脉动压强为参数的控制指标：

ΔPm≤150kPa相当于67.5k Pa脉动压强均方根。若给出最大容许上举力，式（2.80）和式（2.81）都可用于确定底板稳定的控制指标。

2.3.6.2 底流消能消力池底板稳定的控制指标

关于底流消能消力池底板稳定的控制指标，文献[50]给出脉动压强均方根为入池流速水头的5%～10%。即

按这个指标，本研究的消力池入池流速为40m/s，相应流速水头约为800k Pa，由此可得脉动压强均方根应控制在40～80kPa。下面根据试验结果，对脉动压强与上举力的量化关系进一步解读。

由前面试验得出的结果为：

得：

式（2.84）表明，单位面积上的最大上举力大致为5倍的脉动压强均方差。若控制指标为σp′≤40k Pa，则相当于最大上举力为200k N/m2（20t/m2）。

上述控制指标没有考虑板厚和锚固水平对稳定性的影响。按文献[25]中的底板抗浮稳定计算模式，得：

式中：G′为单位面积板块的浮重；A为单位面积板块的锚固力。

取式（2.84）的平均值代入式（2.85），则：

式中：d为板块厚度。给定K f，根据板厚和锚固力则可确定脉动压强具体数值。