底板尺寸对稳定性的影响分析

消力塘底板破坏的主要原因是板块上表面动水压力沿着缝隙进入板块下表面，因上下表面动水压力的相位差在板块上产生强大的上举力，最终导致板块失稳。消力塘底板尺寸会影响底板上下表面脉动压力的相关特性，从而导致底板水流上举力的不同并影响其安全性。本节通过分析水流脉动压力相关尺度、消力塘底板尺寸、上下表面脉动压力的相关特性对底板水流上举力的影响，基于此对消力塘底板块尺寸对稳定性的影响进行了探讨。

已知面脉动上举力的标准差σr为：

式中：σp、σq分别为底板块上、下表面面脉动压强的标准差；ρpq为底板块上下表面面脉动压强互相关系数。显然水流上举力不但与上下表面的脉动压力强度有关，还与上、下表面脉动压力的相关特性密切相关。考虑两种极端的情况，如图2.61、图2.62所示。第一种情况（图2.61）：涡旋的空间尺度大于或等于板块的尺寸，这样，上表面受同一个涡旋控制，两个缝隙入口处的压力脉动完全相关，若上下表面的脉动压力强度相等，上下表面脉动压力能够相互抵消；第二种情况（图2.62）：涡旋的空间尺度远远小于板块的尺寸，两个缝隙入口处的脉动压力部分相关（存在相位角差φ1-φ2）或者完全不相关，这种情况可能会产生最大的上举力。下面分别从水流脉动压力相关尺度、消力塘底板尺寸、上下表面脉动压力说明。

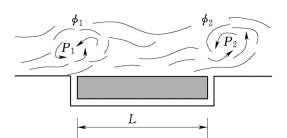
图2.61　大尺度涡旋

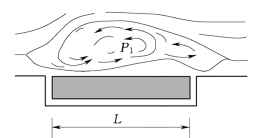
图2.62　小尺度涡旋

2.3.4.1 上下表面脉动压强的相关关系

将板块上下表面各个测点的脉动压力均方根值σ用跃首流速水头ρv2/2无量纲化，得出各个测点脉动压强系数，即Cp′=σρv2；同样定义脉动上举力强度系数F′=Fσ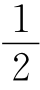ρv2（Fσ为上举力标准差），最大上举力强度系数F+=F maxρv2（F max为上举力最大值）。

脉动压力的空间积分尺度决定了两个测点脉动压力相关的最大距离。沿水流纵向的脉动压力积分尺度的数学表达式为：

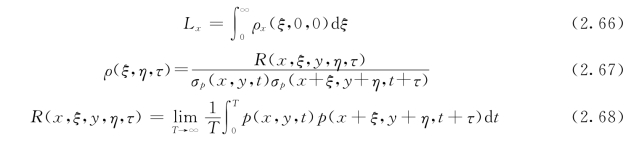
式中：p（x，y，t）为某点的脉动压力。

由于水跃强滚区内紊动特性相当复杂，目前还处于初步探索阶段，只能利用紊流统计理论近似给出L x。即在水跃底部纵向布置一系列传感器，将测量到的脉动压力代入式（2.66）～式（2.68）计算得到。

2.3.4.2 上下表面脉动压强的相关系数

板块下表面的脉动压力来自于上表面，上下表面脉动压力的瞬时互相关系数的大小体现了上下表面脉动压力的同步性好坏。上下表面同步性越好也即其相互抵消的可能性越大，可能的最大上举力就越小，如式（2.64）所示。鉴于点脉动压力易于测量，上下表面面脉动压力间的瞬时相关系数与点脉动具有相同的变化规律，因此以点脉动的相关关系来代替面脉动，不会影响分析的结果。

图2.63以脉动压力空间积分尺度与底板块尺寸的比值Lx/L作为X轴，按式（2.67）计算的上下表面中点脉动压力的瞬时互相关系数作为Y轴。图2.63中可以看出随着L x/L的增大，上下表面脉动压力的相关系数逐步增大。

2.3.4.3 上下表面脉动压强的转化系数

由于缝隙对涡旋的选择作用和沿程损耗，脉动压力沿缝隙传播到底板块的下表面时，其强度发生衰减。定义下表面点脉动压强系数的平均值与上表面点脉动压强系数的平均值的比值为上下表面点脉动压强转换系数Cd，即

将脉动压力空间积分尺度与底板块尺寸的比值L x/L作为自变量，上下表面点脉动压强转换系数Cd作为因变量，图2.64表示了两者间的关系。从图2.64中可以看出随着L x/L值的增大，上下表面脉动压强转化系数逐步增大。

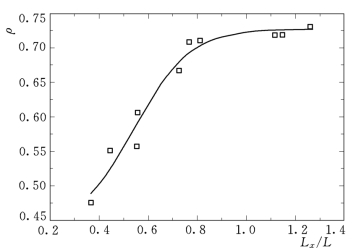
图2.63　上下表面中点脉动压力的瞬时相关系数

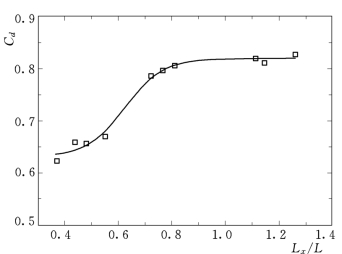
图2.64　上下表面点脉动压强的转化系数

2.3.4.4 脉动压强相关尺度、板块尺寸对上举力的影响(https://www.xing528.com)

从图2.63和图2.64可以设想在极限情况下，当脉动压力空间积分尺度与板块尺寸比值趋向于正无穷，或者说底板块的尺寸无限缩小到一个点，则脉动压强转换系数和瞬时相关系数都将趋向于1，此时上下表面的上举力出现最小值；当脉动压力空间积分尺度与板块尺寸比值趋向于零，或者说底板块的尺寸无限扩大，则脉动压强转换系数和瞬时相关系数将趋向于零，此时，上举力也出现最小值；在这两个极限情况之内，上举力在某一点应该达到最大值。

上举力试验结果证实了这一推测，图2.65给出了不同尺寸板块脉动上举力强度系数与L x/L之间的关系。可以看出，脉动上举力强度随L x/L的增大而增大，在L x/L=0.80左右达到最大值，之后又随着L x/L的增大而减小，形成一种类似高斯分布的曲线型式，瞬时最大上举力也有相似的分布，如图2.66所示。刘沛清[45]在冲坑底部岩块脉动上举力的试验研究中，其脉动压力积分尺度为2m左右，采用的板块尺寸分别为2m、4m、6m，其L x/L位于图2.66曲线的左半部，因此得出了岩块尺寸越大，最大上举力越小的结论。Fiorotto[46]在进行板块上举力和尺寸优化试验研究时，认为防护结构在其他设计因素允许的情况下，其横向尺寸应该尽可能小而纵向尺寸应尽可能大。Fiorotto确定的板块最优尺寸的横向尺寸位于图2.70、图2.71的右半部，而纵向尺寸则位于左半部。

图2.65　脉动上举力强度与L x/L的关系

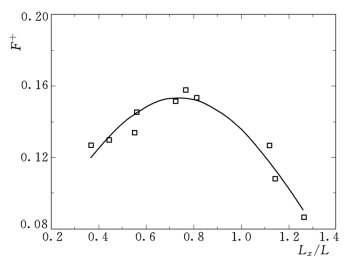
图2.66　最大上举力强度与L x/L的关系

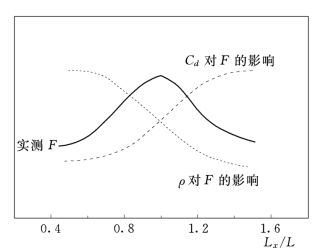
图2.67　上下表面相关特性对上举力的影响

图2.67解释了产生这种现象的原因：当防护结构块相对较大时（L x/L很小），一方面可以降低上表面的平均压强，另一方面可以减小上下表面点脉动压强转换系数，增强结构安全性。当防护结构块相对较小时（L x/L很大），虽然上表面的平均压强和上下表面脉动压强转换系数都很大，但是由于防护结构块的尺寸远小于脉动压力空间积分尺度，结构块上下表面脉动压力的相关性、同步性很好，其作用可以相互抵消。而当防护结构块的尺寸和脉动压力空间积分尺度相当时，上表面的平均压强和上下表面脉动压强转换系数仍然比较大，同时上下表面脉动压力在时间上有一个相位差，这样就可能发生在下表面压力最大时，上表面的压力最小，造成结构物瞬时承受巨大的上举力。

在水工模型试验中，相对于上举力，底板块上表面的点脉动压强是最容易测量的物理量。如果要通过上表面点脉动压强估计上举力，就需要建立与之对应的转换关系。上举力的转换系数Cp定义为：

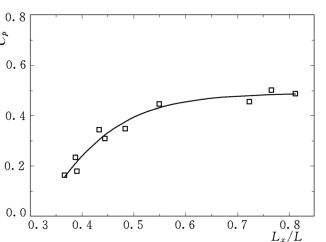
图2.68　脉动上举力与点脉动压强的转换系数

图2.68给出了以Lx/L为横坐标的上举力与点脉动压强之间的转换系数，该图可以估算消力塘底板最大脉动上举力。

2.3.4.5 板块尺寸的优选设计

图2.69给出了实验中水跃区脉动压力纵向空间积分尺度的沿程变化。图中可以看出，急流区和跃尾的脉动压力积分尺度较大，水跃强滚区的积分尺度较小。若考虑1∶100的模型比尺，板块尺寸在10m左右，则在急流区和跃尾L x/L远大于1，板块避开了可能的最大上举力；而在跃中强滚区个别位置L x/L接近于1，板块可能遭受到最大上举力。因此，进行板块尺寸设计时，板块的尺寸位于两条虚线以外的区域是较为安全的，并且可以考虑在不同区域采用不同的板块尺寸。

图2.70为某高拱坝消力塘表中联合泄流工况下脉动压力积分尺度的模型实验统计结果（已按重力律换算成原型值），以冲击滞点为横坐标0点（H z为上下游水位差）。对挑跌流消力塘来说，射流冲击区范围内的脉动压力积分尺度较小，壁面射流区的积分尺度较大，射流冲击区与壁面射流区的过渡区域存在L x/L≈1.0的可能性。图中可以看出，该工程采用的板块尺寸（14m）与脉动压力积分尺度比值为1.0的位置位于上游壁面射流区，这里上表面的脉动压力较小，因此不会产生太大的脉动上举力。下游由于两道坝的阻断作用，具有和消力塘同尺度的大涡旋没有形成，脉动压力积分尺度较板块尺寸低得多，所以下游板块都处在较安全的区域。

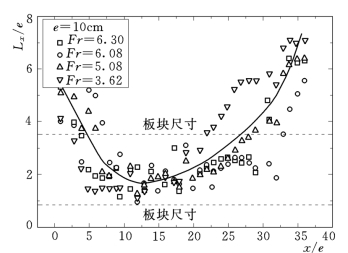
图2.69　脉动压力积分尺度沿程分布

图2.70　消力塘脉动压力积分尺度沿程分布

目前，我国工程上采用的消力塘底板设计标准主要参照日本一些工程（一般是中小工程），这些工程消力塘水垫浅，动水压力最大的区域涡旋尺度小，板块10m左右的尺寸较涡旋尺度已大的多，因此板块尺寸是偏于安全的。我国的工程多是大型甚至巨型工程，运行时水垫深，动水压力大的区域涡旋尺度也大，Lx/L易于处在接近1的危险区域，因此在工程设计中，防护结构块的尺寸应该在允许的条件下相对于脉动压力空间积分尺度尽可能取得大一些，或者小一些，而不要取在与脉动压力空间积分尺度相当的范围内。

综上，通过分析消力塘平底板板块尺寸对稳定性的影响，得到如下几点认识：

（1）相同的工况条件下，板块尺寸越接近脉动压力空间积分尺度，下表面的脉动压强就越接近上表面，上下表面脉动压强的相关性越好。

（2）相同的工况条件下，脉动上举力强度随L x/L的增大而增大，在L x/L≈1.0时达到最大值，之后又随着L x/L的增大而减小，形成一种类似高斯分布的曲线型式。

（3）在工程实际中，为了底板的稳定，防护结构板块尺寸应该在允许的条件下相对于脉动压力空间积分尺度尽可能取得大一些，或者小一些，而不要取在与脉动压力积分尺度相当的范围内。