水流脉动压力幅值的点面转换方法

随着高山峡谷修建高坝的发展，采用经坝身挑流、坝顶跌流泄流的趋势，将有增无减。因而射流作用在河床或护坦上的时均压力和脉动压力是否可能引起河床严重冲刷、护坦失稳破坏以及能否激起轻型结构强烈振动等问题令人关注。本节结合二滩水电站局部水工模型实验成果，进行理论分析，探索二元射流作用在河床或护坦面上脉动壁压特性，进而根据点、面脉动壁压的相关性，推导出点、面脉动壁压转换的简易的解析表达式[13，34]。

2.2.3.1 点脉动壁压幅值计算

1.点脉动壁压强度最大值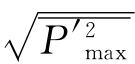

射流作用下河床面或护坦面上的点脉动压力是随机现象，但产生点脉动壁压强度最大值的位置却是确定的，压力最大点称压力滞点。影响脉动压力的物理量很多，但因本实验水流雷诺数大[Re=u 0 d 0/v=（0.63～1.75）×105]，研究的冲击压力脉动问题、射流入水角和掺气变化不大，故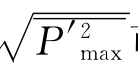可看成是水舌入水速度u0、入水水舌厚度d 0、下游水深h和水的密度ρ的函数，经量纲分析得：

整理实验资料并用曲线拟合，得到图2.25。在实验范围内（h/d 0＞13），其经验公式为：

上式是在入射角为60°～65°时得到的。考虑脉动压力是由流速脉动产生的，以及在滞点动能变成压能的事实，对于其他入射角θ，式（2.36）可近似改写成：

2.点脉动壁压强度分布

在工程不仅要知道滞点处脉动壁压强度最大值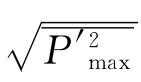，而且还关心滞点上、下游点脉动壁压强度分布。用各点脉动壁压强度与滞点脉动壁压强度最大值的比值和各点到滞点距离x与有效水垫深度h c0的比值，对所测各点脉动壁压强度加以整理，得到图2.22。

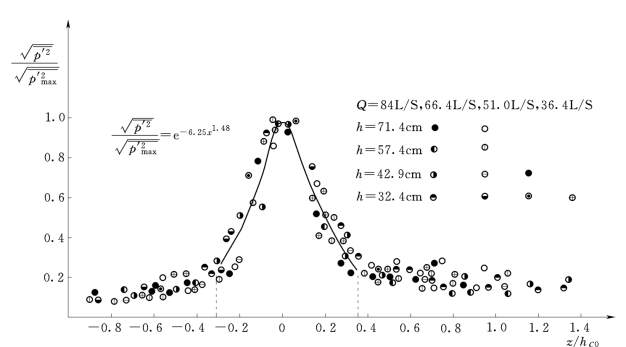
图2.22　点脉动壁压分布

冲击区点脉动壁压强度分布可表达如式（2.38）。

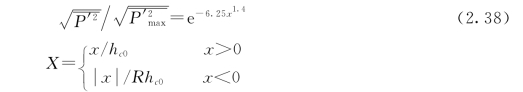
式中：x值在滞点下游为正；R为水垫中射流扩散不对称系数，R随水舌入水角θ增大而增大。

由图2.22可以看出，在滞点附近存在一个点脉动壁压强度及其梯度较大的区域，其范围x/hc0约为-0.32～0.35，即所谓射流冲击区。冲击区外上、下游点脉动壁压强度及其梯度较小的区域，可视为射流影响区。在滞点上游射流影响区，脉动壁压强度随X增加而减小，当X在0.355～1.0范围内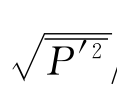，由0.24变到0.10，在滞点下游射流影响区；当X在0.35～0.75范围内，脉动壁压强度增加的数值不大，取其外包值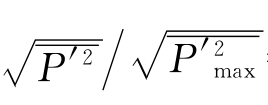=0.25，这一点与淹没水跃起始段临近最大脉动壁压强度点的脉动壁压的特征相近，当X超出0.75～1.5范围，脉动壁压沿程递减，这也与淹没水跃后半部所显现的脉压特征相近。

3.点脉动壁压振幅分布特性

由大量试验结果可知，射流作用下点脉动壁压的概率密度函数是符合正态分布的，只有在大流量、小水深时，滞点附近的点脉压的Cs和Ce值与正态值有偏离。面脉动壁压实验成果表明，面脉动壁压强度的振幅分布比点的有更好的正态性，在滞点也具有较好的正态分布特性。

2.2.3.2 面脉动壁压幅值计算

工程设计最感兴趣的是面脉动壁压，但实验（或计算）得出的点脉动壁压强度比面的偏大，不宜直接用于工程设计。因此，存在一个由点转换成面脉动壁压的问题。近年来，都采用经验折减系数和做实验的办法来解决。本文利用相关分析原理，结合实验资料，求出计算面脉动壁压的解析表达式。

1.点面脉动壁压相关分析

在长为l、宽为b矩形脉动壁压场内，取出一个微小面积d A=d x d y，点面脉动壁压关系为：

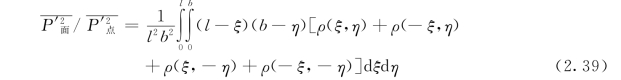(www.xing528.com)

式中：ρ（ξ，η），ρ（-ξ，η），…是点互相关系数。

式（2.39）就是经相关分析得到的点面脉动壁压转换的关系式。下面的问题是寻找点互相关关系的规律。

2.点脉动壁压互相关系数

点脉动壁压互相关函数不仅与两点距离有关，而且还与方向有关。为了方便，在推求脉动壁压互相关关系时，先把它分解成顺水流方向和垂直水流方向的互相关系数，再分别探讨，最后再综合求出点互相关关系的分布规律。

根据点互相关系数定义，顺水流方向相距ξ的两点互相关系数可写成：

垂直水流方向相距η的两点互相关系数可写成：

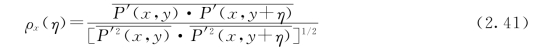
据此，将冲击区各点脉动壁压相互关系成果点绘成图2.23、图2.24，经拟和后得到射流冲击区点脉动壁压相互关系表达式。

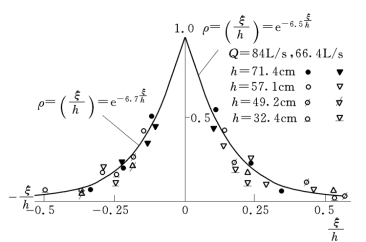
图2.23　顺水流向点脉动相关系数

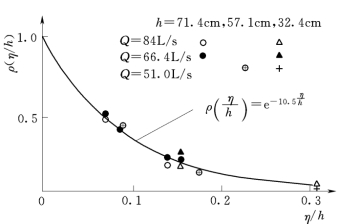
图2.24　垂直水流向点脉动相关系数

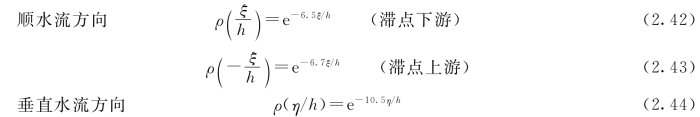
由图2.23和图2.24看出，在二元射流冲击区点脉动壁压互相关系数大小主要受下游水垫和两点相对位置控制，而受上游水位影响相对较小。还可以看出，冲击区点脉动壁压顺水流方向和垂直水流方向互相关系数分布基本上具有对称性，即

式中：α、β为常数；α取6.5；β取1.05；其他字母代表意义与前同。

式（2.48）是在均匀流场情况下得到的，对于射流只需P′采用积分区间内点脉动壁压的平均值，就可以利用式（2.48），很方便就计算出面脉动壁压。

图2.25　点、面脉动壁压转换折减系数

点、面脉动壁压转换系数C′p定义为：

利用式（2.49）计算了各实验工况的C′p值，并将它与实测的面脉动压力求得的C′p值都点绘于图2.25上。可以看出，计算曲线同实验点基本是吻合的，与崔广涛等[36]人给出深水垫时挑流冲击下游河床的C′p值为0.4～1.0、A.斯波里亚里克等[37]人给出消力池底板上的不恒定冲击力的C′p为0.4以及黄涛[38]根据丰满原型观测给出的C′p值为1/3～1/2进行比较，说明式（2.48）、式（2.49）的计算精度可满足工程需要。