模型开发：岛屿宽度和水力传导系数对透镜体厚度的影响

（1）参数设置与模拟

构建代数模型的第一步是量化降雨及珊瑚岛主要的水文地质特征如岛屿宽度、水力传导系数、不整合面深度、礁盘的存在等对淡水透镜体厚度的影响。方法是利用计算软件对每一参数，在保持其他参数值不变的条件下，对其变化范围内的一系列值进行模拟计算。在模型开发中，降雨变化范围为2.5～5.5 m/a，但对于改变其他参数进行模拟计算时，降雨量保持常数为4 m/a。上层含水层水力传导系数的变化范围为25～500 m/d，但对于改变其他参数进行模拟计算时，上层含水层水力传导系数保持常数为50 m/d。不整合面深度的变化范围为8～16.5 m，但对于改变其他参数进行模拟计算时，不整合面深度保持常数为16.5 m。对每一岛屿宽度在具有和不具有礁盘的条件下进行模拟计算，礁盘用一层厚1 m的低水力传导系数（K＝0.05 m/d）的地质单元来表示，并从岛屿的海洋一侧延伸到岛屿的中部。

每一系列的模拟计算均在岛屿的宽度范围（150～1 100 m）内进行，以定量研究岛屿宽度的影响，年回补量取年降雨量的50%。在所有模拟计算中，下层含水层的水力传导系数均取500 m/d。透镜体的底部边界取为500 mg/L氯离子等浓度面（2.5%海水浓度）。

为了定量研究在平均季节气候条件下和严重干旱条件下透镜体的水力特性，Bailey等还进行了时变模拟计算，计算中使用的回补率随时间变化，由西太平洋密克罗尼西亚东西Caroline地区的气象数据获得。和恒态模拟系列计算类似，时变模拟计算也分背风岛和迎风岛，并都在设定的岛屿宽的范围内进行。

（2）降雨量、岛宽和不整合面深度数值计算结果拟合

Bailey等人选择5个不同宽度的岛屿在7种不同降雨量回补条件下进行恒态模拟计算，将计算获得的透镜体中央厚度Zmax作为年降雨量和岛屿宽度的函数绘图，如图8.3（a）所示，图中L后括号内的数值为岛屿宽度。由图可见，对于每一宽度的岛屿，随着年降雨量的增加，透镜体中央厚度Zmax按指数增加，但趋于一定值L。这表明当透镜体的厚度趋于L时，降雨量增加对Zmax增加的影响逐渐降低。因此，数值计算结果可用一趋于极限的指数衰减函数来拟合，方程为：

式中　Zmax——透镜体中央厚度，m；

　　　L——Zmax的最大值，m；

　　　R——年降雨量，m/a；

　　　b——由岛屿宽度确定的拟合参数，如图8.3（b）所示。

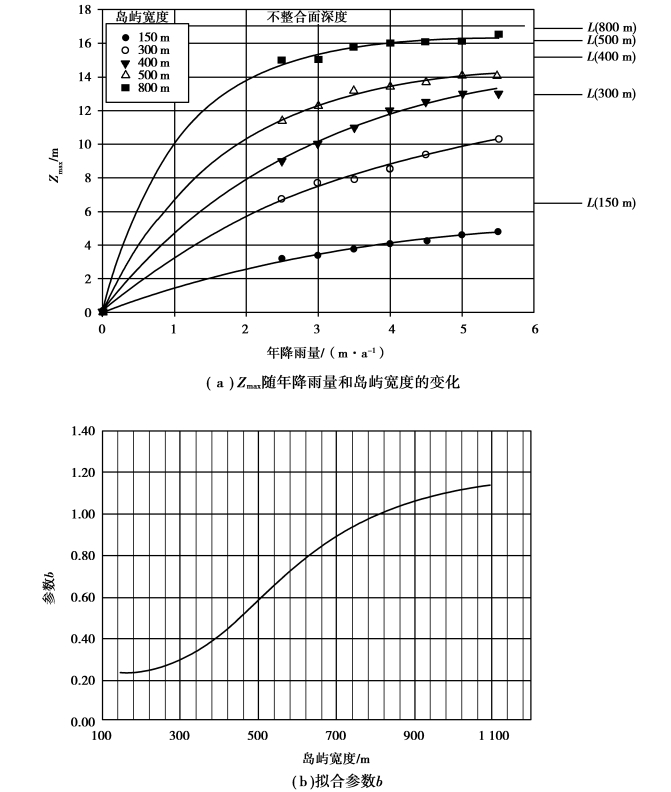
图8.3　透镜体最大厚度Zmax的拟合曲线

式（8.15）中，Zmax的最大值L是岛屿宽度和不整合面深度的函数，如图8.4所示。当岛屿宽度较小时，随宽度增加，L快速增加；当岛屿宽度较大时，随宽度增加，L增速减缓，趋于不整合面的深度。一个宽度为800 m、年降雨量较大的岛屿，透镜体的底部可能向下延伸至不整合面，L的值与不整合面的深度相同，为16.5 m。然而，对于小岛，无论年降雨量为多少，透镜体的底部都不会达到不整合面的深度。如宽度为300 m的小岛，最大透镜体厚度L值为13.0 m，宽度为200 m的小岛，L为9.3 m，均小于不整合面深度。因此，大岛（如800 m以上宽度岛屿）的透镜体厚度受不整合面深度的限制；而对于小岛，如200 m宽度岛屿的透镜体厚度，则受其宽度的限制。

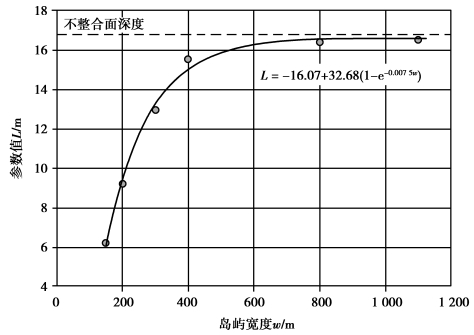
图8.4　不同宽度岛屿的L值

图8.4所示的透镜体中央厚度的最大值L随宽度变化的曲线可用下面指数关系式拟合：

式中　L——Zmax的最大值，m；

　　　w——岛宽，m；

　　　y0，a，d——拟合参数。

由于不整合面深度是大岛透镜体厚度的限制因素，根据式（8.16），当岛屿宽度趋于无穷时，L的极限是y0＋a，等于不整合面的深度ZTD，即

由上式解出a，并代入式（8.16），得：

式中　L——Zmax的最大值，m；

　　　w——岛宽，m；

　　　ZTD——不整合面深度，m；

　　　y0——拟合参数，y0＝-16.07；

　　　d——拟合参数，d＝0.007 5。(www.xing528.com)

这样，对于给定岛屿宽度和不整合面深度，用式（8.18）就可以计算最大可能的淡水透镜体厚度L，再将这一值代入式（8.15），就可求得在给定的回补率、岛宽、不整合面深度条件下淡水透镜体的最大厚度。不同岛屿宽度、不同不整合面深度时的L值也可由图8.5确定。

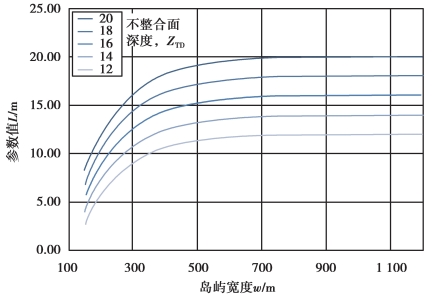
图8.5　透镜体最大厚度L值曲线

（3）水力传导系数与礁盘影响

含水层水力传导系数对透镜体厚度有明显影响。选取不同宽度的岛屿，在不同水力传导系数条件下，对淡水透镜体的演变进行恒态数值模拟，计算结果如图8.6所示。

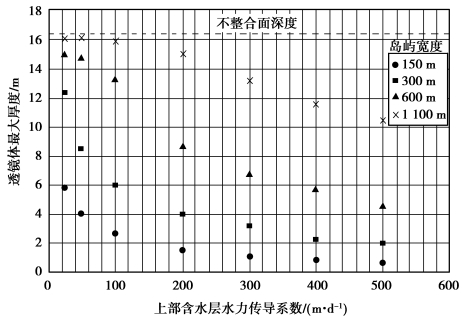
图8.6　水力传导系数对透镜体最大厚度的影响

模拟结果表明，透镜体厚度随水力传导系数的增加显著地减小。还可看到，透镜体厚度随含水层水力传导系数的增加而减小的速率受岛屿宽度的影响，岛屿越小，影响越显著。这是由于小岛上透镜体更强烈地受到水力梯度变化的影响。

水力传导系数对透镜体厚度的影响，可以在式（8.15）中引入一个水力传导系数参数S来表示。式（8.15）是根据水力传导系数为50 m/d的模拟计算结果得到的，可将这一水力传导系数条件下算得的透镜体最大厚度对应的水力传导系数参数S作为1，根据图8.6的数据，计算其他水力传导系数条件下不同宽度岛屿透镜体最大厚度的水力传导系数参数S值，绘成如图8.7的关系曲线，方便使用。这样，对应于不同的水力传导系数，透镜体最大厚度Zmax可按下式计算：

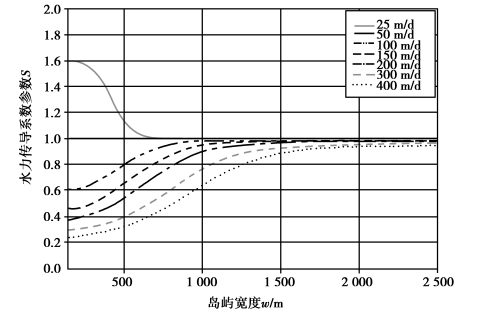
图8.7　不同岛宽时的水力传导系数参数S

图8.7表明，S是含水层水力传导系数和岛屿宽度的函数。对于一定的水力传导系数和不同的岛屿宽度，S按比例决定了淡水透镜体的厚度。高水力传导系数的参数S值小，对应了一个薄的淡水透镜体。

根据一系列不同宽度的岛屿，在有无礁盘时的数值模拟计算结果，用类似的方法可得到礁盘参数C，如图8.8所示。

礁盘参数C表示具有礁盘岛屿的透镜体厚度与没有礁盘岛屿透镜体厚度之比。礁盘的影响是随岛屿宽度的增加，透镜体厚度的增值减小。由图查得礁盘参数C后，在式（8.19）中再乘上一个因子C，即可表征礁盘对透镜体厚度的影响：

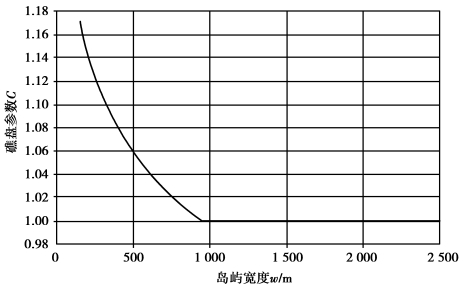
图8.8　礁盘参数C变化曲线

珊瑚岛若无礁盘，C值等于1.0。如图8.8所示，礁盘使小岛的透镜体增厚，一个宽200 m的小岛，C值为1.14，代入式（8.20）将增大淡水透镜体的厚度。但对宽度大于1 000 m的岛屿，礁盘对透镜体厚度的影响可以忽略。

这样，式（8.20）连同式（8.18）便考虑到了所有相关的水文地质特征：年降雨量R、岛宽和不整合面深度（通过L表达）、水力传导系数（通过水力传导系数参数S表达）、礁盘（通过礁盘参数C表达）对透镜体厚度的影响。如果不知道含水层水力传导系数，那么对于环礁上的岛屿，水力传导系数可以分别用背风岛50 m/d和迎风岛400 m/d的水力传导系数的值来计算。对于侧向岛，无论处于环礁岛的迎风还是背风部分，都可以用50 m/d和400 m/d间的值来计算。模拟计算表明，淡水透镜体对不整合面的深度和含水层的水力传导系数最为敏感，其次是岛宽和年降雨量。礁盘对透镜体厚度的影响较小。

（4）干旱影响

季节变化特别是偶发的干旱事件对透镜体的厚度及几何外形有重要影响，这种影响可以在式（8.20）中引入一个无量纲干旱因子D来表达。干旱因子D的定义是：在某一时段内，按月均或按日降雨量进行时变模拟计算，将算得的月透镜体厚度除以恒态模拟计算得到的透镜体厚度，便得到无量纲的干旱因子。这样，干旱因子实际上表示了在特定月份透镜体厚度占恒态条件下透镜体厚度的分数。根据干旱因子的含义，考虑干旱影响的代数模型就可用下式表示：

式中，D为干旱因子。

Bailey等人应用西太平洋密克罗尼西亚西Caroline的Yap和东Caroline的Pohnpei两地区，1977—1999年间的日降雨量进行时变模拟计算，确定了这一期间的干旱因子。选择这一时段主要是为了考察该区域1977年强烈的EI Niño现象，以及随之而来的1988年后半年剧烈的干旱期间透镜体的损耗。他们给出了东、西Caroline地区5个典型时期：1个月（干旱开始），6个月（干旱峰值），12个月（6个月恢复期），18个月（12个月恢复期），24个月（18个月恢复期），背风岛和迎风岛的干旱因子，见表8.1。

表8.1　东西Caroline区域不同大小的背风岛和迎风岛的干旱因子

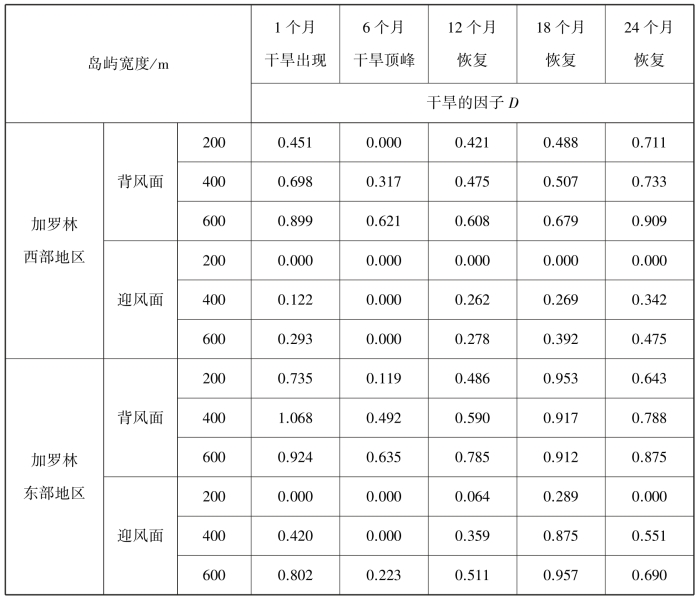
由表中的干旱因子，可看出透镜体厚度的变化，如西Caroline区域一个宽600 m的背风环礁岛，6个月的干旱因子为0.621，也就是透镜体的厚度为恒态时透镜体厚度的62.1%，而到第24个月，干旱因子是0.909，表示此时透镜体的厚度为恒态时透镜体厚度的90.9%。这说明在干旱期间透镜体变薄，出现干旱峰值后，要恢复到干旱前的状态，需要1.5 a的时间。

引入干旱因子D后，就可以计算干旱和后干旱恢复期的Zmax。由于上述D值的确定依赖于1997—1999年密克罗尼西亚环礁岛屿的数值模拟结果，与岛宽、岛屿位置和1997—1999年El Niño及后El Niño期间的雨量分布有关，因此，上述D值只能用来表示1997年El Niño对密克罗尼西亚环礁岛屿淡水透镜体厚度的影响。不过，因为1998年密克罗尼西亚的干旱与有记录的其他干旱相比极为严重，所以对类似的严重干旱事件在干旱峰值月份，式（8.21）依然能给出Zmax的近似值。这样，对于未来的El Niño事件，要评估密克罗尼西亚和类似的环礁岛屿的水资源，式（8.21）也是有用的。