突变界面倒锥的作用及应用

突变界面倒锥的近似计算方法是Dagan和Bear提出的。他们假设：含水层多孔介质均匀各向同性；淡水和海水两种流体为不可压流体，由一突变的几何界面分隔；流动服从Darcy定律。在每一流体流动区域中，流动速度势满足Laplace方程，在这些假设条件下，由小扰动法求得了倒锥的近似解，它是时间和距离的函数。取坐标如图7.7所示，锥面到初始界面的距离，即锥面方程Z（r，t）为：

式中，R′和t′为无量纲径向距离和无量纲时间：

式中　Z——锥面到初始界面的距离，L；

　　　Q——抽水速率，L3T-1；

　　　Δρ/ρf——两种流体的无量纲密度差。Δρ＝ρs-ρf，ρs为海水密度，ρf为淡水密度，取ρs＝1 025 kg/m3，ρf＝1 000 kg/m3；

　　　d——井底与t＝0时界面的距离，L；

　　　r——距井的距离，L；

　　　n——孔隙率；

　　　Kz，Kx——垂直和水平方向上含水层对淡水的渗透系数，LT-1；

　　　t——抽水开始起算的时间，T。

在抽水井正下方，r＝0，式（7.1）简化为：

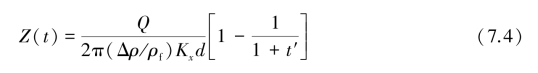
将式（7.3）代入式（7.4），并对时间t求导数，得到抽水井下方锥的上升速率：(www.xing528.com)

式中，A和B是由几何关系以及含水层和流体决定的常数：

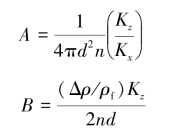
式（7.5）表明抽水井下方倒锥界面上升速率随抽水速率增加而增大。对一个给定的抽水速率，倒锥界面上升速率与锥面升高Z呈线性关系，直线斜率为-B，即锥的升速随升高高度而减少。

在一定抽水速率下，当t→∞时，得到最终升高Z（r）max、Zmax，由方程式（7.1）和式（7.4）：

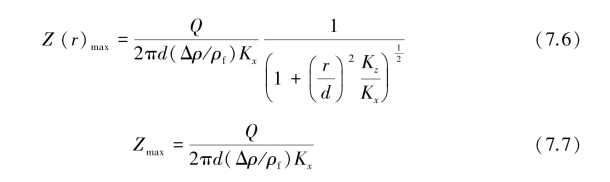
式（7.6）和式（7.7）中，Zmax为在新平衡位置，锥面的最终升高。Zmax正比于抽水速率Q。Zmax和Q的这一线性关系在临界升高Zcr之下成立。Bear和Dagan 1964年所作的模拟试验表明：当Z/d＞1/3～1/2时，锥面会加速上升，在临界升高Zcr之上时，锥面会突然跃升到抽水井底部。Dagan指出Zmax和Q的线性关系实际上在Z/d＜1/2成立。Bear和Dagan推介使用（Z/d）max＜1/4以保证抽水的安全，并避免受到海水咸化影响。

临界升高Zcr有一个取值范围，Falkland给出这一范围为Zcr/d＜0.4～0.6，并认为计算临界抽水率时，可取Zcr＝d/4～d/3，且这一取值范围偏于保守。井的抽水速率小于临界抽水速率时，不会抽吸到海水，却在一定程度上会受到咸水弥散的影响。但另有学者给出了Zcr的不同取值，Muskat 1964年定义不稳定上升或加速上升区为Z/d＞0.48，临界升高在Zcr/d≅0.60～0.75。

另外，S.Schmorak和A.Mercado在地中海沿岸的Ashqelon地区进行过现场实验。实验场含水层总厚度达70 m，由沙、沙粒与黏土、有机土构成。在实验场开凿一个抽水井，距该井不同距离再开凿5口观测井，在每口观测井的不同深度安装有开孔网。观测井中放入传感器，测量不同深度的电阻率，以获得盐分的分布剖面，监测抽水引起的界面上升和停止抽水后的倒锥消退情况。实验进行了2年多的时间，分别作了两套不同抽水速率和持续时间的实验。实验结果表明：临界升高值Zcr/d的值为0.4至0.6；当Z/D＝1/4～1/3时，倒锥会加速上升。Zcr/d＝0.4～0.6的这一实验值稍高于Bear和Dagan根据海滨取水井建议的1/4～1/3。Zcr表示界面中心的最大允许升高，这一高度上对应了海水与淡水盐分差的50%，此值约为17 500 mg/L的总溶解固体。Zcr＝d/3可以作为抽水速率一个合理的设计标准。实验还表明，计算结果与抽水试验结果吻合相当好，并且伴随着界面上升，过渡带增宽。根据现场实验结果，S.Schmorak和A.Mercado建议临界升高计算公式Zcr＝Θd中的Θ取0.5，该值是现场测得的Zcr/d＝0.4～0.6的平均值。

另外，抽水形成的倒锥在抽水停止后会消退，锥面下降。这是由于淡水透镜体中的淡水重新经过过渡带流向海洋的结果。消退期的锥面高度Z（r，t），可在抽水结束后将抽水井想象成回补井而求得：

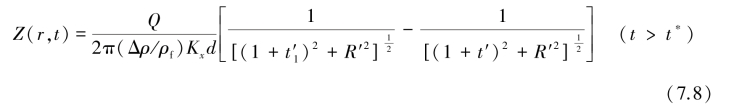
在井的下方，r＝0，式（7.8）简化为：

式中，t*为抽水停止的时间。R′和t′分别由式（7.2）和式（7.3）确定；t′1由式（7.3）用t-t*替代t计算确定。