如何构造差分方程？

回到珊瑚岛礁淡水透镜体数值模拟的差分构造上。设珊瑚岛地下含水层系统已划分为若干个三维网格单元，空间任一点（x，y，z）处的水头为h＝f（x，y，z）。取其中任意一个单元（i，j，k），与其相邻的六个单元分别为（i-1，j，k），（i＋1，j，k），（i，j-1，k），（i，j＋1，k），（i，j，k-1）和（i，j，k＋1），如图6.9所示。按照上述差分的构造方法，某一时间层，如n层上水头h对x、y、z偏微分的差分为：

向前差分：

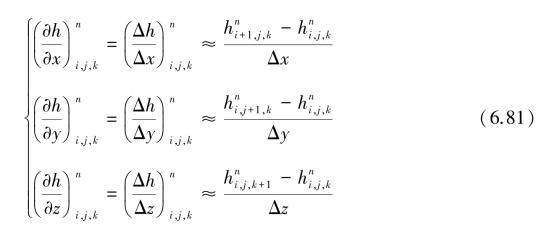
向后差分：

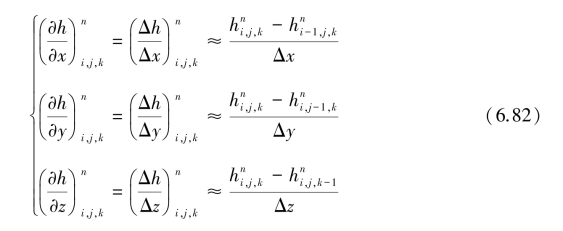
中心差分：

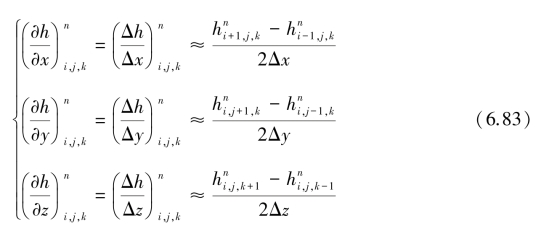
二阶偏导数的差分：

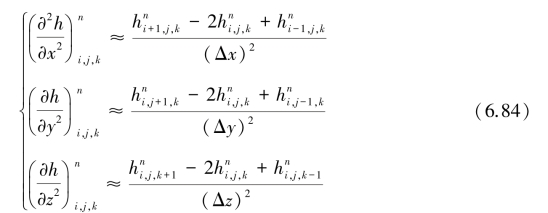
式中　上标表示时间层；下标表示计算单元的位置；

　　　——计算单元（i，j，k）在n时层的水头值；

　　　——计算单元（i＋1，j，k）在n时层的水头值；

　　　——计算单元（i，j＋1，k）在n时层的水头值；

　　　——计算单元（i，j，k＋1）在n时层的水头值；

　　　——计算单元（i-1，j，k）在n时层的水头值；

　　　——计算单元（i，j-1，k）在n时层的水头值；

　　　——计算单元（i，j，k-1）在n时层的水头值。

类似地，n时层计算单元（i，j，k）水头h对时间t偏微分的差分也可表示为：

向前差分：

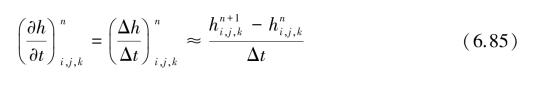
向后差分：

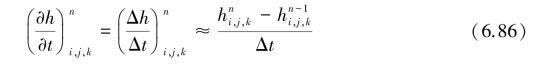
中心差分：

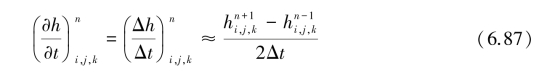
式中　——计算单元（i，j，k）n时层水头值；

　　　——计算单元（i，j，k）n-1时层水头值；(www.xing528.com)

　　　——计算单元（i，j，k）n＋1时层水头值。

应用上述差分公式，就可以用差分代替微分，将偏微分方程改造成差分方程。偏微分方程定义在连续的求解域上，差分方程定义在网格上。将定解条件也离散为网格上的函数关系或函数值后，差分方程加上离散化的定解条件就构成了差分格式。由于用以近似微分的差分有前差分、后差分和中心差分之分，加上在网格节点上构成差分的函数可以在n时间层上取值，也可在n＋1时层上取值，这就导致了各种不同的差分格，其中显格式和隐格式是广泛使用的两种格式。

（1）显式差分格式

显式差分格式是指任一时间层上的节点值可由前一时间层上的已知值表示出来，不需要求解任何代数方程组，只需由初值开始，将已知时间层上的节点值代入差分方程，就可逐一地计算出各时间层上各节点之值，仅需要代数四则运算，数值计算过程简单。

由水流方程式（6.51）：

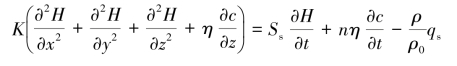
式中，水头H和浓度c对空间坐标偏导数的差分在n时层上取值，对时间t偏导数的差分在n＋1和n时层上取值，根据式（6.83）、式（6.84）和式（6.85），改造方程式（6.51），得到水流方程显格式形式的差分方程：

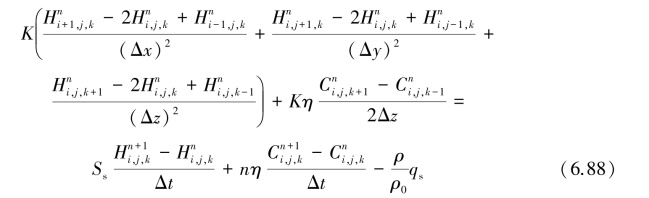
对溶质方程式（6.61）：

在分区计算的条件下，若将Dii视作常数，用与改造方程式（6.51）相同的方法，得到溶质方程显格式形式的差分方程：

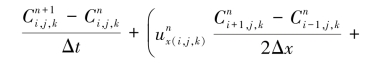
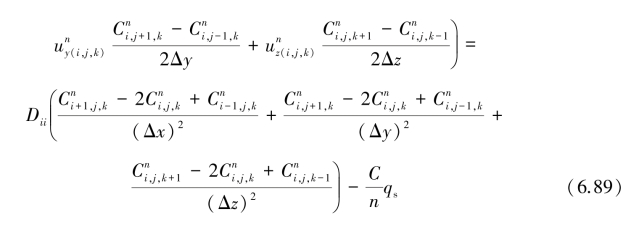
式中，ux、uy、uz是水头的函数，由式（6.17）、式（6.10）和式（6.11）确定。因此，若将n时层上求解域中各点的函数值作为已知值，那么式（6.88）和式（6.89）中仅有，为未知量，可以联立求解。n＋1时层上各点的函数值就由n时层上的值显式表出，即任意时间层节点上的函数值可以由前面时层上的函数值显式表现出来。这种差分格式称为“显格式”。式（6.88）和式（6.89）中，n＝0，1，2，3，…，n＝0表示初值。

显格式计算从n＝1时层开始，这一时层上各点的值都由n＝0时层的值，即初值表示出来。求得第1时层各点的值后，再向第2时层推进，计算第2时层各点的值，依次计算第3时层、第4时层……，直到所需时层各点的值算出为止。

然而，差分方程的解是否是原微分方程定解问题的解？或者说差分格式的解能否逼近原来微分方程定解问题的解？这就涉及差分格式的收敛性和稳定性问题。因为用差分代替微分存在逼近误差，构建差分方程时便产生了截断误差；用差分式格式计算时，同一时层上每一节点处的计算值还受其他节点误差的影响，也受在该点计算过程中数值舍入误差的影响。因此，节点上微分方程定解问题的精确解与差分格式的解之间就存在误差，这一误差是由于微分方程和求解域离散化而带来的，称为“离散误差”，又称“全局误差”。如果空间步长趋于零、计算时层n趋于无穷时，全局误差趋于零，那么差分方程的解逼近原微分方程的解，差分格式便是收敛的，否则是不收敛的。此外，差分方程的求解是按时层顺序一层一层地向前推进的，某一步上产生的误差，会逐层传递下去。对于一个差分格式，如果在计算过程中误差传递的趋势是越来越小，或者始终控制在一个有限的范围之内，则称差分方程是稳定的；相反，如果误差不断积累，使差分计算解与精确解之间的差异越来越大，将精确解湮没，这样的差分格式就是不稳定的。只有收敛、稳定的差分格式才是有价值的。对于一个确定的定解问题，差分格式的收敛性与时间、空间步长和格式本身的类型有关，但通常要直接证明差分格式的收敛性确是十分困难的。普片采用的办法：一是有些问题可以较为容易求得差分格式收敛的必要条件，便可使计算在满足这样的条件下进行，但要注意，这样的条件并不一定是收敛的充分条件；二是通过证明与差分有关的其他一些性质来间接证明差分格式的收敛性，如腊克斯（Lax）等价定理，便是通过证明差分格式的稳定性来间接证明它的收敛性的。在数值计算领域，讨论差分格式稳定性的方法很多，读者可以参阅相关的书籍。

（2）隐式差分格式

上述显格式的求解过程十分简单。但显格式是条件稳定的，因而差分格式的网格步长受到严格限制。这就意味着要加大计算工作量，同时也难以提高计算精度。而隐式差分格式一般是无条件稳定的，网格步长不像显格式那样受到严格限制，有利于减少计算工作量和提高计算精度。

隐式差分格式是指任一时间层上各节点的值，既与前一时间层上的节点值有关，也与同一时间层上相邻节点的值有关，这样各时间层上的节点值就不能由前一时间层上的节点值显式表示，而需要求解一个线性代数方程组。

根据式（6.83）、式（6.84）和式（6.85），对空间坐标的差分在n＋1时层上取值，改造方程式（6.51），得到隐格式的水流差分方程：

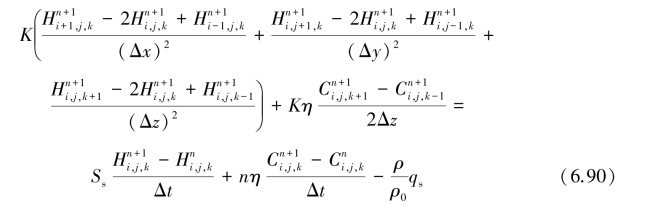
同理，对溶质方程式（6.59）亦采用隐格式：

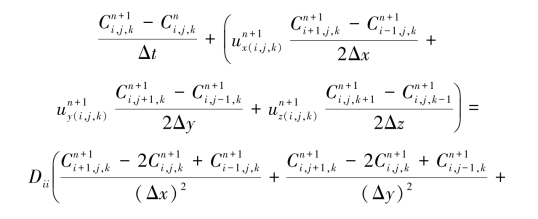
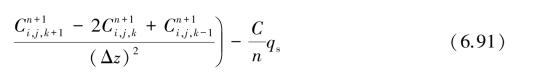
由上两式可以看出，每一节点第n＋1时间层的值是由第n时间层的值和n＋1时间层相邻节点的值一起来表示的。因此，每一时层每一节点上的值，都必须求解一个以该时层上的节点值为未知量的代数方程组，这样逐层求解，最终获得所需时层上各节点的目标函数值。

比较显式差分格式与隐式差分格式，由于隐式无条件稳定、网格步长不受严格限制，又可减少工作量和提高精度，因而是更常使用的一种格式。下述永兴岛淡水透镜体的三维数值模拟即采用隐式差分格式。