离散函数的域、时间与求解技巧

（1）求解域离散

求解域离散指用等间距或不等间距的网格将一个含水层系统划分为一个三维的网格系统，如图6.8所示。例如，用一系列垂直于x轴的平面将含水层沿x方向划分为若干等份，每一等份为一列，列号用j表示，列间距为Δxj；再用一系列垂直于y轴的平面将含水层沿y方向划分为若干等份，每一等份为一行，行号用i表示，行距为Δxi；最后用一系列垂直于z轴的平面将含水层沿z方向划分为若干等份，每一等份为一层，层号用k表示，层间距为Δzk。这样整个含水层被剖分为若干个小长方体，每个小长方体称为“计算单元”。在理论上，同一层中的所有计算单元可以具有不同的尺度，以反映含水层性质在空间上的变化。但在实际工作中，由于单元网格分得足够细小，可以认为每个计算单元内各点有相同的水文地质特性，同时为了计算方便，常使每个同层计算单元具有相同的形状大小，一般为相同的立方体或长方体。每一个计算单元的位置由其行号i、列号j和层号k来表示，即（i，j，k）表示行号为i、列号为j、层号为k的计算单元。i称为“行下标”，沿y轴负方向编排；j称为“列下标”，沿x轴正方向编排；k称为“层下标”，沿z轴负方向编排，如图6.9所示。每个计算单元的体积可以表示为ΔxjΔyiΔzk。上述i，j，k＝1，2，3，…。每个计算单元的水头、溶质浓度和其他参数以该节点处的值表示。边界上节点的值为已知值，由边界条件确定，边界以内的节点称为“内节点”。内节点上的函数值是待求值。

图6.8　含水层空间离散

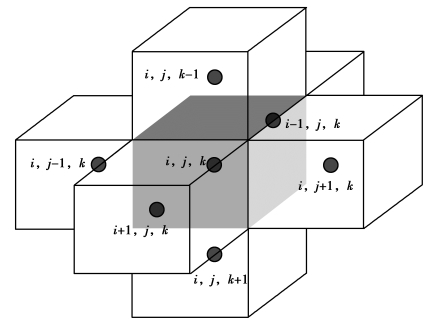
图6.9　计算单元（i，j，k）和其相邻的六个单元

（2）时间离散

从初始时刻起，用一系列时间间隔，即时间步长Δtn将模拟时长分成有限时段，每一时段称为“一时层”，时层的编号以n标记，n＝1，2，3…。同一时层内流动参数不变。

（3）函数离散

空间离散后，就可将未知函数在节点处对坐标的偏微分用差分表示，称为“函数的离散”。函数离散的基础是Taylor展式。设有水头分布函数h＝f（x，y，z），只要f（x，y，z）连续可微（在实际问题中，这个条件常常是满足的），就可以沿着某一方向，如x轴的正向或负向，用Taylor级数展开：

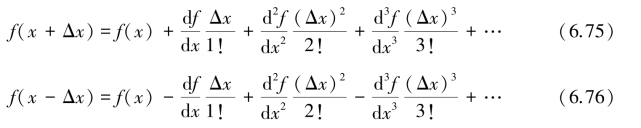
由式（6.75）和式（6.76）得：(www.xing528.com)

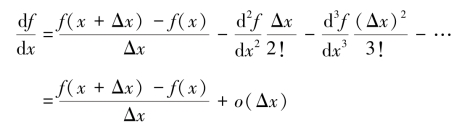
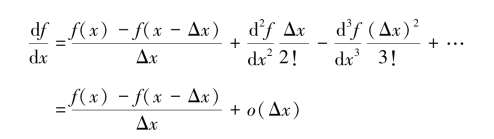
略去一阶无穷小，分别得到一阶导数的近似表达式：

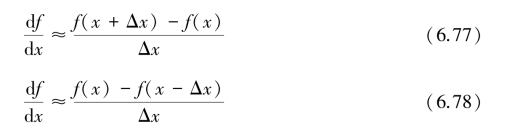
这两式实现了用差分来表示微分。式（6.77）用x和前面一点x＋Δx的函数值之差构成的差分来表示微分，称为“前差分”；式（6.78）用x和后面一点x-Δx的函数值之差构成的差分来表示微分，称为“后差分”。在差分表达式中，由于省略了一些小项，与真值比较会有误差，称为“截断误差”，可以用截去的级数项中最大的一项±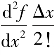来表示。这项与Δx同量级，只要Δx足够小，产生的误差便会任意小，从而保证了差分替代微分的正确性和可靠性。

除了前差分和后差分这两种格式外，还有一种差分，称为“中心差分”，可由式（6.75）减去式（6.76）得到：

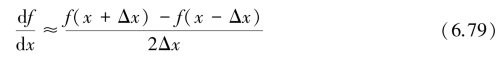
构造中心差分时，截去的级数项中最大的一项为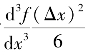，截断误差与（Δx）2同量级。与前、后差分比较，精度提高了一级，达到二级精度。这不难理解，构造中心差分时，用了x-Δx、x和x＋Δx三个点的函数值。

上述是一阶导数的差分表达式，还可以构造二阶导数的差分表达式。将式（6.75）与式（6.76）相加，得到：

不难看出，二阶导数的差分表达式的截断误差也与（Δx）2同量级。