模拟区域的定解条件及其重要性

淡水透镜体三维数学模型的主管方程是二阶非定常偏微分方程，描述了渗流流动和溶质运移的一般规律，方程的解有无穷多组，称为“泛定方程”。要得到适合于所研究问题的唯一解，即要获得模拟区域上渗流流动和溶质运移的特定规律，必须提出适定的定解条件，使问题成为一个定解问题。因此，正确确定模拟区域的定解条件尤为重要。定解条件包括边界条件和初始条件。边界条件是指模拟区域几何边界上的目标函数必须满足的值；初始条件是指起始时刻目标函数的状态，以指明非稳定过程是从何种状态开始，通常取该时刻为零时刻，即t＝0。就淡水透镜体的三维数学模型而言，边界条件表达了水头或渗流量以及溶质在模拟区域边界上的水力特性和浓度分布。初始条件表达了水头和溶质在模拟区域各点上起始时刻的分布。边界条件和初始条件可根据现场勘测或实验研究得到，在一些情况下，也可根据经验人为给出某种假设，提出相应的数学关系式作为定解条件。

对于定常问题，运动过程与时间无关，定解条件只有边界条件。这种仅取决于边界条件的流动问题称为“边值问题”。而对于非定常问题，则边界条件和初始条件缺一不可，这类问题称为“初值问题”。淡水透镜体三维变密度地下水流属初值问题。

（1）边界条件

三维变密度地下水流的边界条件用于表述水头H或流量q在边界上的取值条件，反映了边界内模拟区流动与外部的联系与相互作用，边界因模拟区域的不同而有不同。如前所述，二维流动问题中的边界是平面域上的封闭边界线，或有限个孤立边界点及边界线；三维地下水流的边界则是空间区域的边界面，或有限个孤立边界点及边界面。通常，任何边界条件都包括两方面内容：确定边界的几何形状，确定边界上目标函数（因变量）或其导数满足的关系。对于三维区域，边界几何形状可以表达为：

F（x，y，z）＝0，此为几何边界不随时间改变条件下的表达式；

F（x，y，z，t）＝0，此为几何边界随时间改变条件下的表达式。

在地下水流研究中，很多情况下实际的几何边界较为复杂，难以找到一个准确的连续函数来描述，这时可对边界进行概化，用平面或简单的曲面来近似；或者在数值计算过程中，对边界进行离散，用一组边界上的点来表述。当研究珊瑚岛礁淡水透镜体时，因珊瑚岛由珊瑚从海底向上增长、经骨骼和各类生物碎屑堆积胶结而成，矗立于海洋之中，四周被海水包围，这种情况下的边界便可分为三个部分：岛上地表、侧向壁面、底部平面，如图6.3所示。前两部分是明确的界面，底部边界则具有一定的随意性，因为珊瑚岛底部深达千米以上，底部边界取在何处合适要依岛屿地质构造而定，好在全球的珊瑚岛集中分布在太平洋、印度洋热带海域和墨西哥湾有暖流经过的洋面，有着相同的地质形成过程和构造特点，即在上层全新世地层和潜伏其下的更新世地层之间存在不整合面，不整合面之下地层在漫长的地质年代中受到海水强烈侵蚀，孔隙溶洞极其发育饱含海水，底部边界就可取在不整合面下一定深度的地方。

图6.3　淡水透镜体边界示意图

三维变密度地下水流的边界条件包括水流边界条件和溶质运移边界条件。

1）水流边界条件

在淡水透镜体的地下水流研究中，在实际应用意义上，水流边界条件可分为三类：

①定水头边界

在边界上给定测压管水头H（x，y，z），对于三维的情况可写为：

式中，Γ1为模拟区域边界，f（x，y，z）、f（x，y，z，t）为已知函数或已知值。流动区域流体与边界外流体连接时就是定水头边界。在地下水流动中，饱和多孔介质与河流、湖泊或海洋相连接的边界属于这类边界，边界上的测压管水位就是河流、湖泊或海洋的水位，如图6.3所示。图6.3中AB和CD段上所有点的侧压管水头都取为H0。给定水头的边界问题称为第一类边值问题，也称“Dirichlet问题”。

②定流量边界

在这类边界Γ2上，垂直于单位面积的流量qn为已知值：

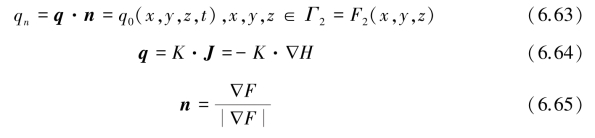
式中　q——比流量矢量，m/d。由Darcy定律确定；

　　　K——水力传导系数张量，m/d；

　　　H——水头，m；

　　　n——边界曲面外法线单位矢量；

　　　q0（x，y，z，t）——已知函数或已知值，如地表单位面积上的补给量。

在定流量边界中，有一类边界，其上不存在流量交换，称为“隔水边界”。如图6.3中的BC段，该段在不整合面之下足够深的地方浸没于海水中，事实上不存在水量交换，因此可视为隔水边界。于是：

对于各向同性介质(www.xing528.com)

上式变为：

或

定流量边界问题也称“第二类边值问题”或称“Neumann问题”。

在淡水透镜体地下水运动研究中，还有一种特殊的边界——潜水面边界。它是多孔介质孔隙内水和空气的界面，如忽略毛细管带水的存在，潜水面为一突变界面，属于有入渗补给的非稳定界面。潜水面的位置是未知的，可通过模拟计算得到最终的稳定位置。

2）溶质运移边界条件

溶质运移边界条件包括三种类型：第一类边界，给定浓度的边界，这类边值问题也称“Dirichlet问题”；第二类边界，给定弥散通量的边界，这类边值问题也称“Neuman问题”；第三类边界，给定溶质通量的边界，这类边值问题也称“混合边界问题”，即“Cauchy问题”。

①第一类边界，在模拟期间沿边界Γ1给定浓度值：

式中，C1（x，y，z，t）为沿着Γ1的浓度值，可随时间变化。

②第二类边界，垂直于边界Γ2方向上的弥散通量已知：

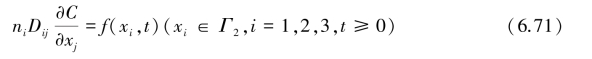
式中，ni为界面Γ2上外法线方向单位矢量n在xi轴方向上的分量，f（xi，t）为沿着Γ2的已知函数，可随时间变化。

③第三类边界，在边界Γ3上给定溶质通量：

式中，qi为比流量矢量q在xi轴方向上的分量，g为沿着Γ3的总通量（弥散和对流）的已知函数，可随时间变化。

（2）初始条件

初始条件用以表示在选定的某一初始时刻，透镜体中的水头分布和浓度分布，这一时刻常取为t＝0。

水流的初始条件为：

式中，H0（x，y，z）为研究区t＝0时的已知水头值，xi∈Ω，Ω为研究区域，i＝1，2，3。

浓度的初始条件为：

式中，C0（x，y，z）为研究区t＝0时的浓度值。

需要指出，初始时刻并非淡水透镜体的生成时刻，因为透镜体的生成时刻既无法确定，也没有必要。事实上，初始时刻是可以根据需要在一定条件下任意选定的时刻。