地下水变密度流主管方程及其关系式

（1）地下水流主管方程

在变密度流中，取直角坐标和介质微元六面体，如图6.1所示。微元六面体各边长分别为Δx1、Δx2、Δx3，与对应坐标轴平行。设流体密度为ρ，流速为v，在各坐标轴上的分量分别为v1、v2、v3。根据质量守恒，可导出变密度流的连续性方程；再运用Darcy定律，便可导出地下水流主管方程。

图6.1　地下水流微元六面体示意图

考虑各方向上单位时间内进出微元六面体的流体质量：x1方向：

类似地

因此，单位时间内进入与流出微元六面体的总质量差为：

设多孔介质孔隙率为n，则微元六面体内单位时间内增加的质量为：

若微元六面体内存在源汇，强度为qs，则根据质量守恒，微元六面体内单位时间内增加的质量应等于单位时间内进入与流出微元六面体的总质量差，与单位时间内单位体积内源qs产生的质量ρqsΔx1Δx2Δx3的和，即

整理得到变密度地下水流的连续性方程：

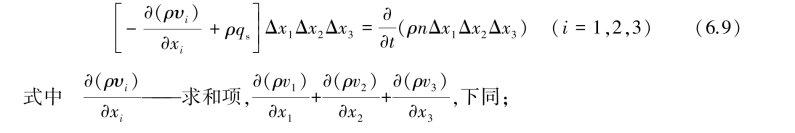
　　　qs——单位时间内、微元六面体单位体积多孔介质源产生的体积流量。qs正表示源，负表示汇，s-1；

　　　x1，x2，x3——直角坐标，对应于通常所使用的x，y，z坐标，在下面的公式推导中，对此将不加区别；

　　　ρ——流体密度，kg/m3；

　　　vi——渗流速度，m/d，i＝1，2，3。

多孔介质中渗流运动方程是由Darcy定律反映的流速与水力坡度间关系的方程，其数学表达式为：

式中　q——比流量向量，等于渗流速度v，m/d；

　　　K——渗透系数，又称“水力传导系数”，是综合反映多孔介质、渗流流体力学特性的一个参数，与多孔介质结构、流体的密度有关，具有速度的量纲，m/d。在非均匀各向异性介质中，K是一个二阶张量；

　　　J——水力坡度，无量纲。

式中　H——测压管水头，H＝p＋，m；

　　　▽——哈密尔顿算子，▽＝k；

　　　γ——容重，γ＝ρg，N/m3。

由前所述，q＝v，有：

在双组分流体（淡水＋海水）的变密度流中，密度随空间变化，p，γ均为（x，y，z）的函数：

因为▽γ≪▽p，所以

式中　k——渗透率，反映多孔介质传导流体的能力，m2，在非均匀各向异性介质中，k是一个二阶张量；

　　　μ——水动力黏滞系数，kg/（m·s）。所以

不失普遍性，写为分量的形式：

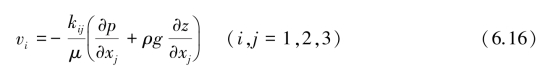
当研究盐分弥散时，需用多孔介质中的真实平均流速ui。渗流速度vi与ui有如下关系：

式中　ui——流体在多孔介质孔隙中的平均流速，m/d；

　　　n——多孔介质孔隙率。

将式（6.16）代入式（6.9）：

在等温条件下，变密度流中，流体密度ρ随压强p和浓度c改变，孔隙率n随压强改变，压强p随时间和空间位置而改变，即

式中　c——混合流体浓度，kg/m3；

　　　t——时间，s。

另外，由于地表以下含水层介质受到上覆岩层、水以及地表建筑物等垂向荷载压力的作用，且与侧向范围广阔相比，垂向范围小，容易变形，所以，通常只考虑垂向压缩，忽略侧向粒间力的作用。因此，可将Δx1，Δx2设为常数，仅考虑垂向变形。这样，式（6.19）右边第一项可展开：

设α为多孔介质压缩系数，β为流体压缩系数。在等温条件下，根据压缩系数的定义，流体压缩系数为：

式中，v为流体体积。

因为在温度t为常数时，ρv＝const，d（ρv）＝0，-，则

在仅考虑透镜体含水介质垂向压缩的条件下，设作用于饱和含水介质上的总应力为σ，固体骨架承受的应力为σ′，介质孔隙中流体静压力为p，则

式中，σ′也称有效应力。

同样，在等温条件下，多孔介质压缩系数可定义为：

式中，vs为介质骨架体积。vs与介质孔隙体积vv之和等于多孔介质总体积vb：

于是：

对于选定的微元六面体，vb＝Δx1Δx2Δx3。由于假设Δx1，Δx2为常数，由式（6.24）：

含水层埋藏于地表之下，作用于饱和含水介质上的总应力为σ可假设为常数，由式（6.23），得：

将式（6.29）代入式（6.28），得：

由式（6.27）：dσ′＝-，得到：(www.xing528.com)

假设骨架的变形很小，可以忽略不计，即

由式（6.32）和式（6.33），得：

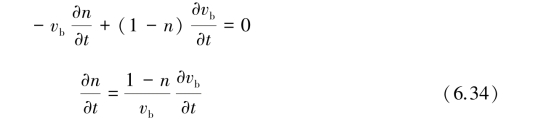
由式（6.31）、式（6.34）和式（6.23），得：

因为σ＝const，则

由此得到：

根据贮水率的定义：

将式（6.22）、式（6.28）、式（6.37）和式（6.38）代入式（6.20），得：

将式（6.39）代入式（6.19），得：

分析上式中的流体动力黏性系数μ和密度ρ。淡-海水混合流体在珊瑚沙砾中流动时，温度无明显变化，流体动力黏性系数μ可视为常数，其值取为淡水动力黏性系数；而密度ρ则可近似表示为溶质浓度c的线性函数：

式中　ρ——混合流体密度，kg/m3；

　　　ρ0——淡水密度，取作参考密度，ρ0＝1 000 kg/m3；

　　　c——混合流体中的溶质浓度，常取为氯离子Cl-1的浓度，kg/m3；

　　　cs——与海水密度ρs对应的浓度，kg/m3；

　　　ε——密度差相对比率，ε＝。

由式（6.41）得：

式中　η——密度耦合系数。

另外，对于淡水水头H：

对式（6.44）取导数：

将式（6.42）、式（6.45）、式（6.46）代入式（6.40），得：

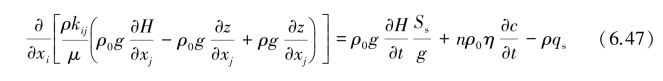
整理上式，应用式（6.41）、式（6.43），得到：

此即为三维变密度地下水流主管方程，式中的Kij为水力传导系数张量K的分量，它与渗透率张量k的分量kij的关系由式（6.15）确定。k和K均为二阶张量。如果取坐标轴的方向与水力传导系数张量K的主方向一致，则

式（6.48）可以化简为：

特别地，对均匀各向同性含水介质，水力传导系数转化为一标量K。式（6.50）可进一步简化：

三维变密度地下水流主管方程反映了水头、密度和溶质浓度间的关系。方程中的qs项代表了源汇的影响，在珊瑚岛礁淡水透镜体的动力学研究中，降雨补给为源，抽水、蒸腾等损失为汇。

（2）溶质运移主管方程

与构建地下水流的主管方程类似，运用质量守恒的原理，可以方便地导出溶质运移主管方程。

仍取直角坐标系和介质微元六面体，如图6.2所示。微元六面体各边长分别为Δx1、Δx2、Δx3，与对应坐标轴平行。研究溶质的运移，需要采用介质孔隙中的真实流速。设流体密度为ρ，溶质浓度为c，介质孔隙中真实平均流速为u，在各坐标轴上的分量分别为u1、u2、u3，弥散系数张量为Dij（i，j＝1，2，3），m2/s，源产生的流体浓度为c*，介质孔隙率为n。

图6.2　溶质运移微元六面体示意图

以下考虑单位时间内进出六面体的溶质之差：

在x1方向上，单位时间内由于对流，进入微元六面体溶质质量为：cu1nΔx2Δx3，流出微元六面体的溶质质量为；在x1方向上，单位时间内由于弥散，进入微元六面体溶质质量为-D1jnΔx2Δx3，流出微元六面体的溶质质量为。单位时间内，同时考虑对流和弥散，在x1方向上，净流入微元六面体的溶质质量为：

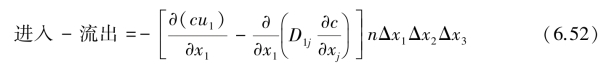
同理，在x2方向和x3方向上，净流入微元六面体的溶质质量为：

单位时间内进入微元六面体的溶质质量为：

另一方面，单位时间内微元六面体中，由于溶质浓度变化而增加的溶质质量为：

考虑源汇的存在，根据质量守恒定律，单位时间内，下式成立：

六面体溶质的增量＝进入六面体的溶质质量＋源增加的溶质质量

整理上式，得到：

多孔介质中的流动通常为不可压缩层流，＝0。于是

式（6.56）转化为：

此即为三维变密度流溶质运移主管方程。如果流场坐标轴与弥散系数张量D主轴一致，则只有Dii不为零，式（6.58）转化为：

在式（6.58）、式（6.59）中，左边第一项表示多孔介质控制单元中溶质质量随时间的变化率，第二项表示溶质随地下水流动的运移量；右端第一项表示由于水动力弥散引起的溶质变化量，第二项表示源项，也可以表示汇，qs为正表示源，否则表示汇，可分别用于表示由于注水、抽水和溶质吸附、解吸等作用造成的溶质增加与减少。在淡水透镜体的开发过程中，用得较多的是抽水，这时式（6.58）、式（6.59）中的qs为汇，表示单位时间内，从单位体积的含水介质中抽取的水量，如果溶质的浓度为c，式（6.58）、式（6.59）右边第二项要作改变，方程分别变为：

式中，-表示单位时间内，从单位体积的含水介质中流失的溶质。

三维变密度地下水流方程（6.48）和三维溶质运移对流—弥散方程（6.59）构成了淡水透镜体三维数学模型的主管方程。