【摘要】:图5.1淡水透镜体微元示意图图5.1中,hf、hs分别为海平面上、下的淡水厚度;qx、qy分别为沿x、y方向流入微元体的体积流量;qx+d qx、qy+d qy分别为沿x、y方向流出微元体的体积流量。将式(5.8)、式(5.9)代入式(5.5),得:为书写方便,以下用h代替hf,表示淡水透镜体在海平面以上的厚度,经整理,得:式或式就是淡水透镜体二维数学模型的主管方程。
在透镜体内建一直角坐标系,x-y平面平行于海平面,z轴铅直向上。在坐标系中取一微元,上表面为潜水面,下表面为淡-盐水界面,底面边长分别为d x、d y,铅直方向高为h,如图5.1所示。
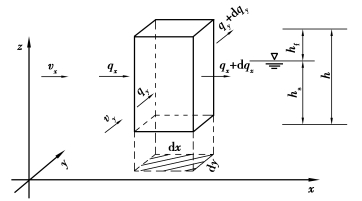
图5.1 淡水透镜体微元示意图
图5.1中,hf、hs分别为海平面上、下的淡水厚度;qx、qy分别为沿x、y方向流入微元体的体积流量;qx+d qx、qy+d qy分别为沿x、y方向流出微元体的体积流量。若Vx、Vy分别为沿x、y方向流入微元体的渗流速度,则沿x、y方向流入与流出微元体的体积流量为:
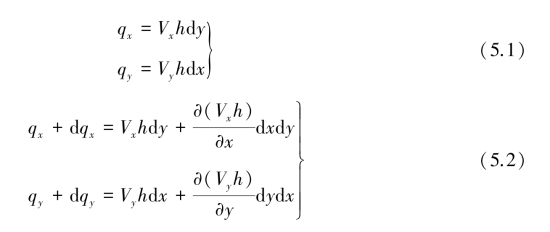
设降水、蒸发和地下径流流失对透镜体形成的补给率为ε(量纲L3/(T·L2)),即单位时间内、单位潜水面积流入的流体体积为ε,且规定水量流入为正,流出为负,则d t时段内通过补给,微元体获得的水量为εdxdydt。如果流入的微元体的水量多于流出水量,微元体内水量将会增加,引起h增大,由此而增加的流体体积为n![]() dxdydt。
dxdydt。
由质量守恒,得到如下关系:
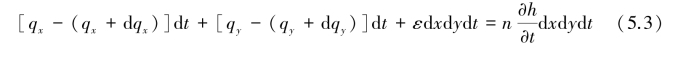
式中,n为有效孔隙率。将式(5.1)、式(5.2)代入式(5.3),有:
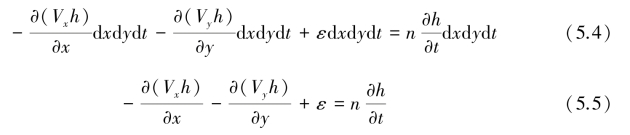 (https://www.xing528.com)
(https://www.xing528.com)
应用Ghyben-Herzberg近似,hs为hf的α倍:
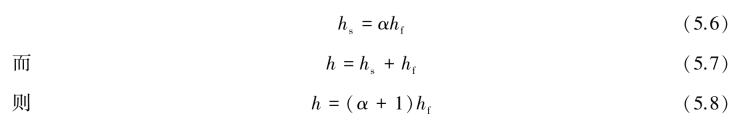
式中,α为Ghyben-Herzberg比率。由Darcy定律:

式中,K为水力传导系数。将式(5.8)、式(5.9)代入式(5.5),得:
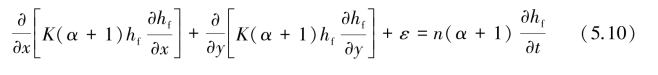
为书写方便,以下用h代替hf,表示淡水透镜体在海平面以上的厚度,经整理,得:
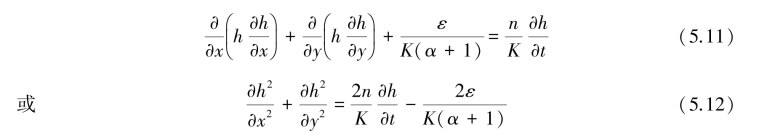
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




