探究Dupuit近似方法的应用

达西定律中渗流速度V与水力坡度J间的线性关系描述了均匀渗流的流动规律，这就意味着符合达西定律的渗流流速彼此平行，潜水面是一平面。然而，实际的潜水面常常是非线性的表面，尤其是淡水透镜体的潜水面是一上突的曲面，潜水面之下的流动便具有垂直方向的分量，使得达西定律的应用碰到困难，也使渗流问题的分析计算变得十分复杂。好在潜水面的坡度一般很小，渗流为缓变渗流，这就为问题的简化提供了可能。1863年，法国水力学家、工程师Dupuit针对缓变渗流，作了一些假设，提出了一种近似理论。设有一缓变渗流，作一铅直平面与流动区域相交，得一截面，截面上潜水面与截面相交为一流线，P是流线上一点，该点的水头为h，流线与水平面的夹角为θ，如图4.2（a）所示。由达西定律，P点的渗流速度Vs为：

式中，d s沿流动方向的流线微元弧长。Dupuit的假设是，对缓变渗流，θ很小，有如下的近似：

当h＝h（x）时，式（4.8）转换为：

(www.xing528.com)

当h＝h（x，y）时，式（4.8）转换为：

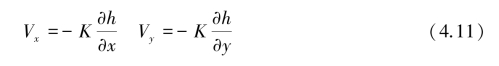
这样，对流线弧长s的偏导数变成了对x或x，y的偏导数。一般而言，弧长s＝s（x，y，z），在式（4.10）和式（4.11）中z不再作为自变量出现，原问题中自变量的个数减少了一个，并且任一竖直线上，各点渗流方向水平，各点渗流速度相等；忽略了流速、压强等流动参量沿竖直方向的变化，如图4.2（b）所示。这不仅使问题得到简化，也将均匀渗流的达西定律推广到缓变渗流，使其在实际渗流运动中得到成功运用。因此，Dupuit近似是淡水透镜体动力学基础的另一重要内容，也是处理二维无压渗流最为有效的方法之一。

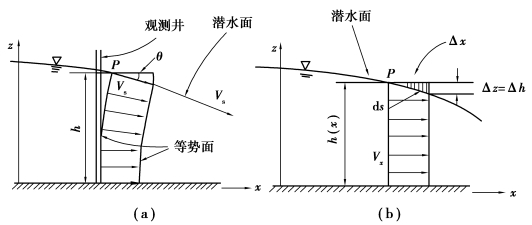
图4.2　Dupuit假设原理图

Dupuit近似忽略了流动在铅直方向的变化，必然带来一定误差。不过，天然条件下，潜水面坡度很小，Dupuit假设带来的误差可以忽略不计。但在潜水面坡度较大时，Dupuit近似就有较大误差。通常，在地下水渗出面附近，在具有垂直补给潜水含水层的分水岭附近、斜坡地带潜水含水层中、抽水井附近和泉水附近的地下水中，渗流在垂直方向上的分量不可忽略，Dupuit近似不再适合。这些地方的流动，应用三维渗流理论来分析。