达西定律：多孔介质中流体的统计规律

流体的运动受作用力的支配，运动规律由运动方程表示。通常运动方程根据动量定理导出，但流体在多孔介质孔隙中流动时，情况就相当复杂，主要是多孔介质孔隙大小不一，孔隙通道蜿蜒曲折、形状多变，使得流速在孔隙中的分布无论大小和方向都不均一。在某一时刻彼此靠近的地下水流质点群，在流动过程中不是都按平均流速运动，而是不断被细分，进入更细的分支，从而使得水流质点逐渐散开，形成按平均流动所预期的范围内流动。加上黏性作用也十分复杂，就很难像一般流体那样可直接由动量定理导出运动方程，只能通过实验总结出另一种形式的描述流体在多孔介质中运动规律的方程，这就是达西定律。

达西定律是一个试验定律，它从宏观角度表达了流体在多孔介质中流动的统计规律。Darcy（全名Henry Darcy）是法国水利工程师，为解决水质净化问题，1856年与工程师C.Rittery一道用直立的均匀沙柱进行了有名的渗流实验，实验原理如图4.1所示。实验装置的主体是一个横截面积为A的圆筒，下部设一滤网，其上填充沙粒，形成长度为L的沙柱，柱顶覆盖另一滤网，当水从上端注入时用以保护顶部沙层，下部滤网则起支撑沙柱的作用。在沙柱上下滤网外侧分别设置进出水管，水管连接一可上下调节水头的容器，连接进水管的容器设溢水管，连接出水管的容器设排水管，将通过沙柱的水流排入量筒中，测量流量Q。另在沙柱上下端设置测压管，用以测量进出水流的作用水头H1和H2。实验时，水流从上端进水管注入沙柱，上下调节出水管容器水面高度，同时测量水头H1、H2和量筒接收的排出水体积及接收时间，计算流量Q。实验表明，通过沙柱的流量Q与横截面积A、进出水流的作用水头差H1-H2成正比，而与沙柱长度L成反比，用公式表示为：

式中　Q——体积流量，m3/s；

　　　K——水力传导系数，m/s；

　　　A——沙柱横截面积，m2；

　　　H1、H2——分别为连接沙柱进出水管容器水面的测压管水头，m；

　　　L——沙柱长，m。

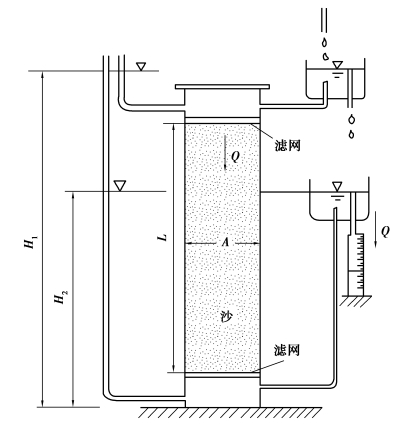
图4.1　Darcy实验原理图

将式（4.1）的两端除以沙柱横截面积A得：

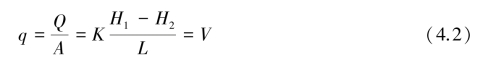
式中，q为单位时间内通过单位面积的水流体积，称为比流量，具有速度的量纲，常称“渗流速度”，用V表示，单位为m/s。

由于流体在多孔介质中流动时只能在孔隙通道中流动，固体颗粒占据的空间是不能流过流体的，而式（4.1）和式（4.2）中的过流断面积A既包含断面上的孔隙面积，也包含固体颗粒占据的面积，因此，式（4.2）中的渗流速度V是假想的流动速度，是假定过流断面上每点全都通过水流时的流动速度。这一速度和多孔介质孔隙中的实际平均流速u有如下关系：

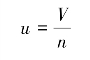
式中，n为孔隙率。考虑到多孔介质中一些孔隙为死端孔隙，流体不能通过；另外，孔隙中在固体颗粒表面，由于分子引力、静电引力的作用，一部分水即结合水被牢牢地吸附在颗粒表面不能流动而占据了部分孔隙空间。因此，多孔介质中流体能流过的孔隙只是总孔隙中的一部分，称为“有效孔隙”，其值用有效孔隙率ne表示。相应地，渗流速度V与实际平均流速u的关系应为：

式中的实际平均流速u在一些著作中称为“渗透速度”。为简单计，以后文中出现的孔隙率均指有效孔隙率，仍用n表示。值得指出的是，渗流速度V与渗透速度u虽只有一字之差，但概念相差很大：渗流速度V是宏观的假想平均流速，渗透速度u是微观真实的平均流速。

式（4.2）中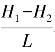，称为“水力坡度”，常用J表示，则：(www.xing528.com)

式中水力传导系数K的物理意义一目了然，可以理解为单位水力坡度作用下的渗流速度。K值随多孔介质和流体种类而变。因此，水力传导系数K是由多孔介质和流体的力学特性共同决定的、反映多孔介质通过流体能力的综合性参数。流体的力学特性由密度ρ和动力黏性系数μ表示；而对珊瑚沙粒这样的松散多孔介质，介质的力学特性由颗粒形状、大小、级配、比表面积、孔隙率以及孔隙通道的弯曲程度等反映。这样水力传导系数K可表示为：

式中　g——重力加速度，m/s2；

　　　k——渗透率或固有渗透率，m2。

根据一系列实验，并与Darcy定律比较，渗透率k可用一经验公式表示为：

式中　c——无量纲比例系数，取值为45～140，黏性沙土取小值，纯沙介质取大值，一般介质取100；

　　　d——有效粒径，取d10，cm。

上述对达西定律的讨论适用于均匀各向同性介质。在多孔介质中，一个物理量的值可以随空间点位或方位的不同而改变，也可以不变。一个物理量的值如果不随空间点位的变化而发生改变，这样的介质称为“均匀介质”，否则称为“非均匀介质”；如果物理量的值不随方向变化而改变，这样的介质称为“各向同性介质”，否则称为“各向异性介质”。珊瑚岛具有双含水层结构，总体而言，含水层属非均匀各向异性介质，不整合面之上的全新世含水层和下伏的更新世含水层具有不同的水力传导系数和弥散度；即使在同一含水层中，在不同方向上，水力传导系数和弥散度也可能取不同的值。当然，在不同问题中，根据具体要求，可以忽略某些差异，作均匀各向同性的近似假设。

以式（4.1）、式（4.4）形式表示的达西定律的特点是体积流量和渗流速度与水力梯度呈线性关系。这一线性关系仅在渗流为层流的条件下成立，渗流为层流的判据可仿照管流流态的判据建立。在管流的条件下，当雷诺数Re＝＜2 000时，工程上将流动归类为层流。在雷诺数Re的计算式中，v是流体的运动黏性系数，表示流体的物理属性；V是管流的平均流度，d为特征长度，常取为水管直径。从作用力的角度看，雷诺数Re计算式的分子代表惯性力，分母代表黏性力。在渗流的情况下，也可以雷诺数Re作为流态的判据，这时的Re可表示为：

式中　v——流体的运动黏性系数，cm2/s；

　　　V——渗流速度，cm/s；

　　　d10——介质的有效粒径，cm。

按照式（4.7）计算的雷诺数Re＜（1～10）某一值时，渗流为层流。

随着渗流速度的提高，线性关系将被打破。J.贝尔将多孔介质中的流动分为三个区：①层流区，是低雷诺数流动区，该区内黏性力起支配作用，线性达西定律成立，层流区上限雷诺数为1～10；②过渡区，该区从低雷诺数黏性力起主要作用的层流状态逐渐转变为惯性力起支配作用的另一种层流状态，进而在该区较高雷诺数时转变为紊流状态，惯性力起主要作用的层流区通常称为“非线性层流区”，过渡区上限雷诺数为100；③紊流区，在该区，Re＞100。这三个区域中，达西定律仅在①区成立。

在珊瑚岛礁淡水透镜体的自然流动过程中，雷诺数较小，满足渗流为层流的条件，线性达西定律成立，从而构成了淡水透镜体动力学基础。