弥散度与观测尺度间关系的研究结果及局限性

弥散度是一个依赖于试验尺度的多孔介质参数，即具有尺度效应。无论室内还是野外现场试验，随着试验介质中流体流经距离的增大，弥散度的取值会越来越大。Gelhar分析了59个不同野外试验数据，发现纵向弥散度的取值范围为0.4～4 m。水平横向弥散度一般比纵向弥散度小一个量级，垂向横向弥散度一般又比水平横向弥散度小一个量级。弥散度的这种尺度效应，加上试验中的误差，使得野外试验的测定值只是一种估计值，仅反映特定条件下溶质的运移属性。

与实验室弥散度的测量一样，野外弥散度的测量也需要在含水介质中投放一定的示踪剂，测量介质中水流动情况下示踪剂浓度的时空分布，根据弥散方程的解通过试算或曲线拟合求得介质的弥散度。实验室内常用的示踪剂是氯化钠（NaCl）。在珊瑚岛上测定珊瑚沙砾的弥散度时，为避免淡水透镜体中氯离子（Cl-）的干扰，可使用其他示踪剂。但要注意，选择的示踪剂应满足无毒、安全、环保、检出灵敏度高、用量少、来源广、价格低等要求。试验方法主要是用井将示踪剂注入含水层，再用井把水抽出来，测试示踪剂的浓度。试验用井可以是单井、双井，甚至是多井。根据测试参数是纵向弥散度、横向水平弥散度或是横向垂直弥散度的不同，地下水流是天然水力梯度作用下的自然流还是人工产生的地下水流，试验有多种方法及变种，但不管哪种方法都较室内测试昂贵和费时。下面介绍一种应用均匀流二维扩散方程结合试验求得纵向弥散度和横向水平弥散度的方法。地下水流可以是天然水力梯度作用下的自然流动，也可以是人工产生的地下水流。

对均质含水层中的均匀地下水流，取x轴的方向为水流方向，则瞬时投放示踪剂的二维扩散方程为：

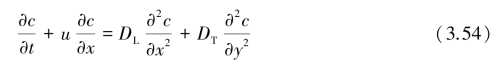
式中，c为示踪剂浓度；u为地下水在多孔介质孔隙中的平均流速，也称“渗流流速”；DL、DT分别为纵向弥散系数和横向水平弥散系数。引入弥散度的概念，DL、DT可表示为：

式中，αL和αT分别为纵向弥散度和横向水平弥散度。式（3.54）解为：

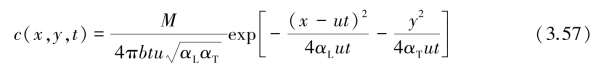
式中，M为t＝0时在坐标原点整个含水层厚度b范围内瞬时投入的示踪剂质量；其余符号同前。

基于式（3.57），Zou S和Par提出了一种由试验数据求弥散度的方法。这种方法需要求解联立方程，但不必预先测定地下水的流向，也不要求观测井和示踪剂投放井在同一流线上，只需大致知道地下水流向即可。图3.27是试验布置示意图，坐标原点O设于投放井，x轴大致指向地下水流方向，1号观测井（x1，y1）和2号观测井（x2，y2）分别位于x轴两侧，与投放井的连线也即距离分别为l1和l2，由Ox轴逆时针转至l1的角γ为正，由l1顺时针转到l2角β为负。由此可得坐标关系式：

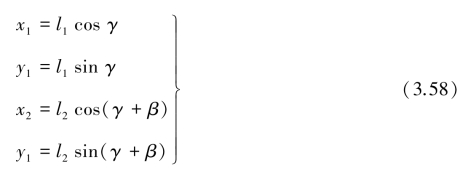
若令：k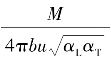＝，则式（3.57）可改写为：

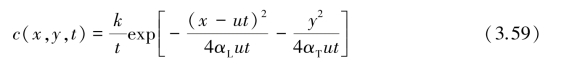
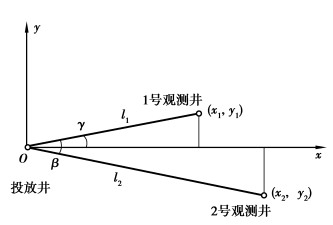
图3.27　试验布置示意图

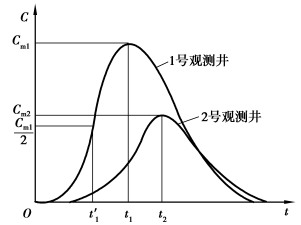
图3.28　观测井中的浓度过程曲线

野外试验时，在投放井中，于t＝0时瞬时投入质量为M的示踪剂如碘（I），然后在1号观测井和2号观测井中测量浓度过程曲线，并在线上读出1号观测井和2号观测井中出现峰值浓度cm1、cm2的时间t1、t2和两井中最大峰值浓度井出现1/2峰值浓度的时间t′1，如图3.28所示。应用求极值的方法，由式（3.59）求得取峰值浓度的时间tm，联合t1、t2和t′1便可建立一组联立方程。由：

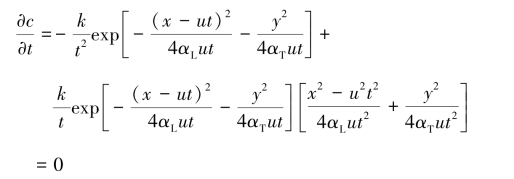
得：

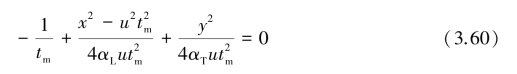
由方程（3.60）解得：(www.xing528.com)

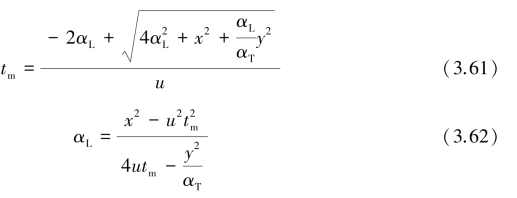
峰值浓度cm为：

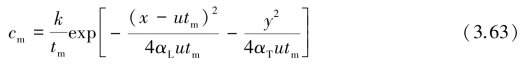
考察式（3.58）和式（3.63），共有5个未知量：γ、αL、αT、k和u，可由以下5个方程组成的方程组求解，即

上述方程组虽是一个封闭方程组，在数学上可以求解，但方程组中包含了超越方程，求解十分麻烦。再考虑到野外试验的难度和成本，工程上大多数问题可以通过已有实测数据整理的资料获得含水介质的弥散度，主要是利用经验公式计算弥散度和查图获得弥散度。

Xu和Eckstein于1995年统计分析了野外测得的纵向弥散度与流程之间的关系，得到如下经验公式：

式中　αL——纵向弥散度，m；

　　　L——观测点与扩散质源点间的距离，m。

式（3.69）反映了弥散度的尺度效应，即随着距离的增大而增大。但也可以发现，当距离L大于几千米后，弥散度随距离的变化很小，这与野外的试验结果是一致的。

之前，1985年Gelhar等综合了59个不同尺度的野外试验数据，给出了如图3.29所示的纵向弥散度与观测尺度间的关系。该图按观测类型和含水介质种类对数据进行了分类，是确定纵向弥散度时被广泛引用的资料。但图中的数据未标明可靠性，他们认为不考虑数据的可靠性并不合适。1992年Gelhar等按可靠性高、中、低对野外试验数据进行了分类表示，给出了弥散度与观测尺度的关系，如图3.30至图3.33所示。由图3.30可以看到对于给定的尺度，纵向弥散度的变化范围可达2～3个量级，不过可靠性高的测试点都集中于图形的下部。图3.31和图3.32给出了横向弥散度与观测尺度的关系，由图可见横向弥散度较纵向弥散度小，也受观测尺度影响；可靠性高的数据表明水平横向弥散度比纵向弥散度至少小一个量级，垂向横向弥散度比水平横向弥散度小1～2个量级。图3.33给出了纵向弥散度αL对水平横向弥散度αTH和垂向横向弥散度αTV的比，图中大的符号表示可靠性高，小的符号表示可靠性低；垂向虚线表示在该点测定了三个方向的主分量，水平虚线表示在数值模拟计算中普遍采用的比率为＝3。鉴于可靠性高的测试点都集中于图形的下部，因此，Gelhar等建议在任何尺度下均使用图中下半部分的弥散度。

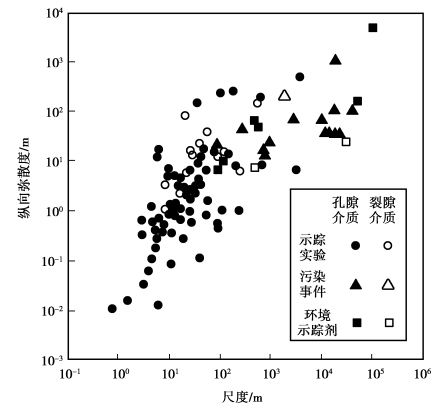
图3.29　纵向弥散度与观测尺度间的关系

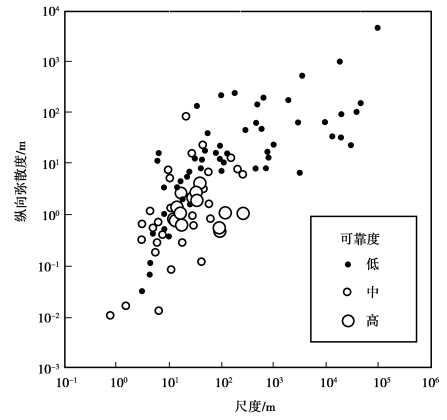
图3.30　按可靠性分类的纵向弥散度与观测尺度间的关系

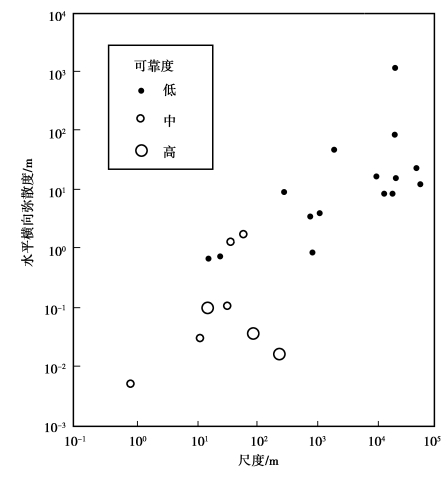
图3.31　水平横向弥散度与观测尺度间的关系

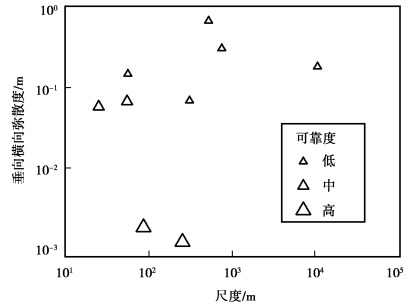
图3.32　垂向横向弥散度与观测尺度间的关系

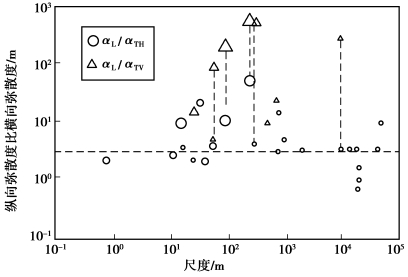
图3.33　纵向弥散度αL对水平和垂向横向弥散度（αTH和αTV）的比