现场测量渗透系数有多种方法,常用双环法、立管法和抽水法。
(1)双环法
双环法是一种传统的现场测量土壤介质渗透系数的方法,由试坑法发展而来。操作过程是:在珊瑚岛上选择地势较高地方,挖一圆形试坑,坑深60~70 cm,坑底直径约100 cm,平整坑底;然后在坑内嵌入两个钢环,使之成同心圆,外环直径50 cm,高15 cm;内环直径25 cm、高15 cm,两环上缘须在同一水平面上。压环时应注意防止珊瑚沙土压实或变形,如扰动过大须重新开挖试坑。之后,在内环及两环间隙内注入清水至满。另取一木支架,上可倒置安放2~4个容量为5 000 mL、装有斜口玻璃管和橡皮塞的供水瓶。调整支架至水平位置,将供水瓶注满清水后倒置于支架上,供水瓶的斜口玻璃管分别插入内环和内外环之间的水面以下。玻璃管的斜口应在同一高度上,以保持水位不变。测试装置如图3.10所示。
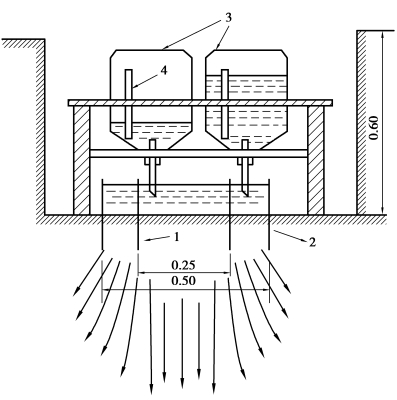
图3.10 双环法试坑渗水试验示意图(图中尺寸:m)
1—内环;2—外环;3—自动补充水瓶;4—水量标尺
试验时记录渗水开始时间及供水瓶的水位。经一定时间后,测量在此时间内由供水瓶渗入珊瑚沙土中的水量,直至流量稳定为止。此后,在1~2 h内测量流出水量至少5~6次,每次测记的流量与平均流量之差不应超过10%。
试验结束后拆除仪器,吸出贮水坑中的水,并在离试坑中心3~4 m以外的地方钻几个深3~4 m的钻孔,每隔0.2 m取土样一个,平行测定其含水率。根据含水率的变化确定渗透水的入渗深度,再按下式计算渗透系数K(cm/min):

式中 Q——稳定渗入水量,cm3/min;
l——试验结束时水的入渗深度,cm;
F——内环渗水面面积,cm2;
Hk——珊瑚沙土毛细压力水头,cm,对珊瑚沙可取5~10 cm,视沙粒粗细而定,越粗越小;
Z——内环水深,cm。
由于入渗深度l获取较为麻烦,并且内环水深z和毛细压力水头Hk与入渗深度l相比是一个小量,作为近似处理,常常略去这两项的影响,渗透系数K按下式计算:

用上述两个公式计算渗透系数K时,体积流量Q要求在环内下渗水量达到稳定时量取,有时这要花很长时间。为避免试验时间拖得太长,可在试验过程中选取两个时段t1、t2(d),累计算出这两个时段内的总入渗量V1、V2(m3),用下式计算渗透系数K(m/d):
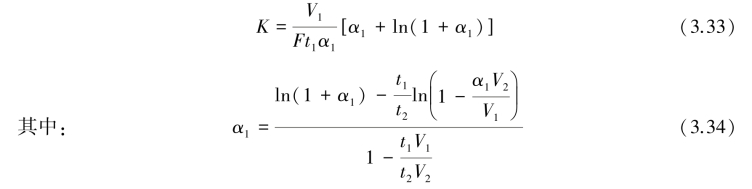
式(3.34)是一个超越方程,式中α1为代用系数,不能直接计算,可在计算机上用试算法求解。
(2)立管法
该法基于降水头渗透仪的测量原理。取一长130~150 cm、内径约10 cm的钢管,将一端管壁切削成楔形,制成测量用的立管。在珊瑚岛上,淡水透镜体通常埋深较浅(如西沙永兴岛),有的地方地面以下0.5 m就有地下水。现场测量时,选择一浅井,将立管从井底铅直插入珊瑚沙土中,埋入珊瑚沙土的管段内便充满了珊瑚沙,如图3.11所示。在这一过程中,立管内珊瑚沙柱受到的扰动很小,可以忽略不计。在管中灌满水,管内沙柱底面的水头近似等于井水位,沙柱顶面的水头则为立管的水面水位。在管内沙柱两端水头差的作用下,管内的水通过沙柱流出,立管内水面就会下降,记录管中水柱下降一定高度所用的时间t(min)。以井水面为基准面,设起始时管中水头为hi(cm),经时间t后,水头下降至hf(cm),立管插入珊瑚沙土的深度为L(cm),则由降水头公式可计算珊瑚沙土的渗透系数K(cm/min):
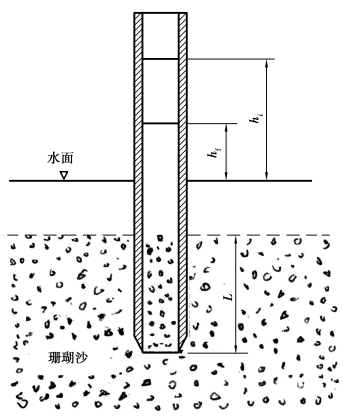
图3.11 立管法测量渗透系数示意图

如果不便用井进行测量,也可选择一测量场地,挖一土坑到出现地下水为止,平整坑底,再将立管从坑底铅直插入珊瑚沙土中,按上述方法操作和计算渗透系数。
(3)抽水试验
1)试验类型
抽水试验在井孔中进行。试验抽水分两种:单孔抽水和多孔抽水。单孔抽水试验仅在一口井孔中进行,这种试验方法简便、费用低廉,但只能粗略地获得渗透系数;多孔抽水试验也是从一口井中抽水,该井称为主井,但在主井之外还要再开凿一定数量的观测孔。试验时,除观测主井的抽水流量和水位降深外,还需要测量观测孔中的水位变化。多孔抽水试验较单孔试验复杂,但获得的资料全、精度高。根据抽水流量和降深是否需要稳定一段时间而分为稳定流抽水试验和非稳定流抽水试验。稳定流抽水试验是在设计的流量下持续抽水一段时间,达到流量和水位降深相对稳定,可以连续变更几个流量,因而有几个稳定的水位降深;非稳定流抽水试验通常是固定一个抽水流量,测量主井和观测孔中的水位随时间而变化。珊瑚岛上的抽水试验从透镜体中抽水,淡水透镜体无上下不透水层,因此,试验用井为非完整潜水井,可采用稳定流抽水试验与非稳定流抽水试验。由于稳定流试验时间长,抽取水量多,要求补给充沛和稳定,而非稳定流抽水试验更接近实际,且能获得更多的水文地质参数,所以,非稳定流试验应用较多。
2)试验设备
抽水试验所用的设备包括水泵、过滤器、排水设备,以及水位、流量等测量仪器。珊瑚岛地下水埋深浅,常选择低压离心泵,这种水泵扬程不大,但出水均匀、调节方便,适合在珊瑚岛上抽水试验使用;珊瑚岛含水层由珊瑚生物碎屑沉积而成,属中粗沙堆积层,需在井孔内壁安装过滤器,起护壁滤水作用;测量仪器主要有水位计、堰箱和孔板流量计等。
3)观测孔布置
当进行多孔试验时,观测孔应以抽水孔为中心、沿半径方向排列,连成观测线。通常,观测线应与地下水流方向垂直或水平。珊瑚岛礁淡水透镜体中央厚、边缘薄,水力梯度一般沿边缘指向中央,地下水流方向较易确定,观测线也就容易布置。观测线取1~4条,如图3.12所示。观测孔一般不少于3个,具体数目由试验方法确定。对于非稳定流抽水试验,如用水位降深s与抽水时间t的关系s-lg t整理试验数据,可布置一个观测孔;若用观测孔水位降深s与抽水孔的距离r的双对数lg s-lg r关系整理试验数据,则观测孔应不少于3个。
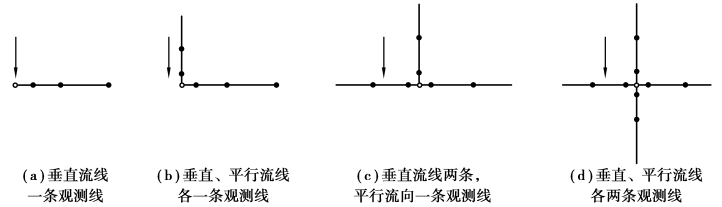
图3.12 抽水井与观测孔平面布置示意图
 —地下水流向;
—地下水流向; —抽水井;
—抽水井; —观测孔
—观测孔
4)试验要求
试验要求观测的参数包括试验前后的孔深、天然水位、抽水量、动水位和恢复水位、气温与水温;稳定流试验时一般要求进行三次水位降深的数据观测,水位降深间距尽量均匀分布,三次水位降深s1、s2、s3与最大水位降深sm的关系大致按s1=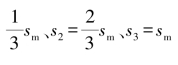 为好,sm可取抽水处透镜体厚度的1/3。试验过程中,水位与流量应同时观测,观测次数先密后疏,如抽水开始时5~10 min观测一次,2 h后每15~30 min观测一次。抽水稳定时间为8~24 h;非稳定流试验通常采用定流量抽水。试验时,要同时观测流量和水位;停止抽水后,要观测恢复水位。观测间隔时间要比稳定流试验的间隔时间短,尤其在开泵和停泵的30 min内,更应加密观测,观测时间可按1、2、3、4、6、8、10、15、20、25、30 min进行。非稳定流的试验时间不需要太长,对珊瑚碎屑这样的砾粗沙含水层,试验延续时间为8~15 h。试验过程中抽出的地下水应排离现场,即水井影响半径之外。
为好,sm可取抽水处透镜体厚度的1/3。试验过程中,水位与流量应同时观测,观测次数先密后疏,如抽水开始时5~10 min观测一次,2 h后每15~30 min观测一次。抽水稳定时间为8~24 h;非稳定流试验通常采用定流量抽水。试验时,要同时观测流量和水位;停止抽水后,要观测恢复水位。观测间隔时间要比稳定流试验的间隔时间短,尤其在开泵和停泵的30 min内,更应加密观测,观测时间可按1、2、3、4、6、8、10、15、20、25、30 min进行。非稳定流的试验时间不需要太长,对珊瑚碎屑这样的砾粗沙含水层,试验延续时间为8~15 h。试验过程中抽出的地下水应排离现场,即水井影响半径之外。
5)资料整理
抽水资料整理分为试验现场资料整理和试验结束后的室内参数计算。
现场整理是伴随抽水试验进行的,主要是对已获得的基本观测数据,如抽水流量Q、水位降深s及抽水延续时间t进行整理,绘制相关曲线,目的是了解流量和水位降深有无异常,观测是否有误,试验是否已达要求。稳定流绘制的曲线主要有Q-s、Q-t、s-t和单位降深涌水量q-s曲线。图3.13和图3.14是常见的Q-s和q-s曲线。其中,曲线Ⅰ代表含水层厚度大、降深小的潜水井流;曲线Ⅱ代表潜水井流;曲线Ⅲ代表从某一降深开始涌水量随降深的增加而增加很少;曲线Ⅳ表示补给衰竭或水流受阻;曲线V通常表示试验有误。对于定流量的非稳定流试验,通常要绘制水位降深s与时间t的相关曲线,如s-t、s-lg t或lg s-lg t曲线;如果观测孔较多,还需绘制观测孔水位降深s与距抽水井的距离r的对数曲线s-lg r。此外,在非稳定流的水位恢复阶段,尚需绘制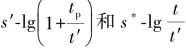 曲线。其中,s′为剩余水位降深;s*为水位回升高度;tp为抽水井抽水开始到停止抽水时的累计时间;t′为从抽水井停抽后算起的水位恢复时间;t为从抽水试验开始至水位恢复到某一高度的时间。
曲线。其中,s′为剩余水位降深;s*为水位回升高度;tp为抽水井抽水开始到停止抽水时的累计时间;t′为从抽水井停抽后算起的水位恢复时间;t为从抽水试验开始至水位恢复到某一高度的时间。
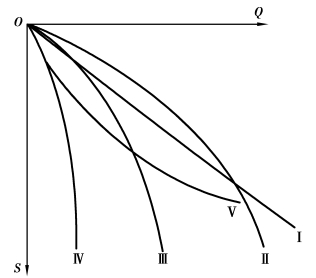
图3.13 稳定流试验的Q-s曲线
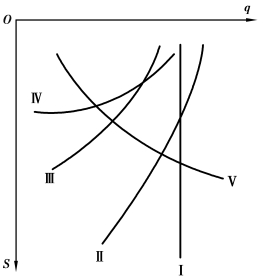
图3.14 稳定流试验的q-s曲线
室内整理是在现场试验结束后,利用试验中获得的原始数据进一步整理求得预期的试验结果。室内整理内容包括综合成果图表绘制、水文地质参数计算和试验报告。成果图表有Q-s、Q-t、s-t和q-s曲线,以及抽水试验成果表等;水文地质参数计算主要有渗透系数K、给水度μ等的计算;试验报告主要是对试验工作进行完整的总结,内容有试验目的要求、试验方法、主要成果、分析讨论和结论。下面介绍渗透系数K、给水度μ的计算:
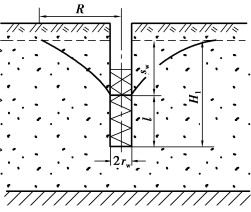
图3.15 单井非淹没过滤器井壁进水
渗透系数K的计算依据抽水试验方法而定。稳定流试验,渗透系数K可用公式计算;非稳定流试验,渗透系数K多用配线法确定,同时还可确定给水度μ。在稳定流试验中,计算渗透系数K的公式也因过滤器是否被淹没以及有无观测孔而有不同。对图3.15所示的单井、非淹没过滤器、井壁进水的情形,渗透系数K(m/d)用下式计算:

式中 Q——稳定抽水时的流量,m3/d;
H1——过滤器底部至潜水面的含水层厚度,m;
sw——井中水位降深,m;
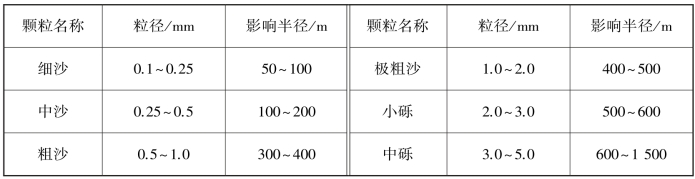
R——影响半径,m,可按珊瑚沙主要颗粒粒径大小选取,见表3.3;
rw——抽水井半径,m。
表3.3 影响半径经验值
如果是单井、非淹没过滤器井壁进水并带有一个观测孔,如图3.16所示,则用下式计算渗透系数K(m/d):
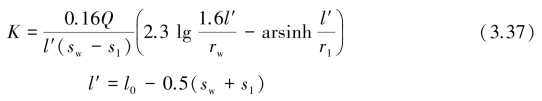
式中 Q——稳定抽水时的流量,m3/d;
l0——过滤器底部至潜水面的含水层厚度,m;
sw——井中水位降深,m;
s1——观测孔中水位降深,m;
rw——抽水井半径,m;
r1——观测孔至抽水井的距离,m。
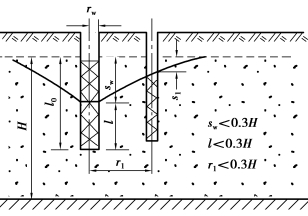
图3.16 单井带一个观测孔非淹没过滤器井壁进水
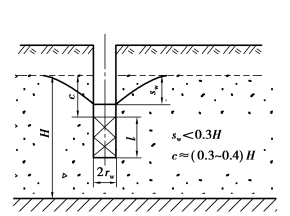
图3.17 单井淹没过滤器井壁进水
如试验过程中,过滤器全部淹没在水中、井壁进水,如图3.17所示,则渗透系数K改用下式计算:

式中,l为过滤器长度(m);其余同前。若抽水井还带有一个观测孔,如图3.18所示,则渗透系数K由下式计算:(https://www.xing528.com)
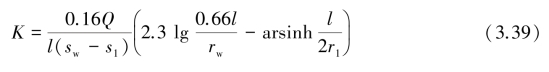
式中各参数同前。
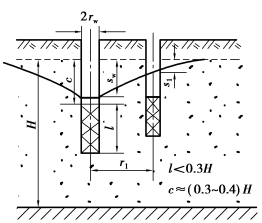
图3.18 单井带一个观测孔淹没过滤器井壁进水
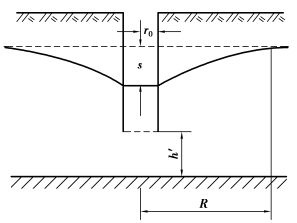
图3.19 大口井
在珊瑚岛上还常用大口井抽水,如图3.19所示。这种抽水井口径大,通常3~5 m,井底进水。当用大口井进行抽水试验时,渗透系数K(m/d)可用下式计算:

式中 Q——稳定抽水时的流量,m3/d;
r0——水井半径,m;
s——井中水位降深,m。
对于定流量的非稳定流抽水试验,试验过程中水位降深随抽水时间变化,根据时间-降深资料就可以确定渗透系数K等相关的参数。非稳定流水文地质参数的确定通常使用配线法,理论依据是在承压含水层条件下求得的泰斯(Theis)方程:


式中 s——观测井降深,m;
Q——抽水流量,m3/d;
T——导水系数,m2/d,T=Kb,b为含水厚度,m;
W(u)——井函数,无量纲,W(u)=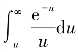 ,其值可在一些有关水文地质的书籍和手册中查找;
,其值可在一些有关水文地质的书籍和手册中查找;
r——观测孔至抽水井的距离,m;
S——贮水系数;
t——从开始抽水算起的时间,d。
上述各物理量的单位也可根据抽水流量的大小适当调整。对式(3.41)和式(3.42)两端取对数:
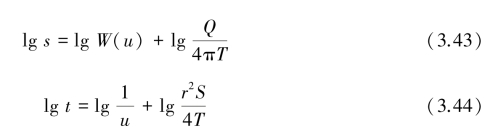
如果有多个观测孔,还可由式(3.42)得到:
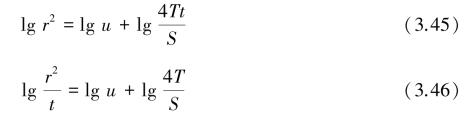
观察式(3.43)和(3.44),可以发现,如果在双对数坐标系中作曲线lg W(u)-lg![]() 和lg s-lg t,那么两条曲线具有相同形状,只是坐标轴有所平移。这就为用图线求解泰斯(Theis)方程奠定了基础,这种方法称为“配线法”。具体步骤:第一,根据井函数W(u)和u的值在双对数坐标纸上作曲线W(u)-
和lg s-lg t,那么两条曲线具有相同形状,只是坐标轴有所平移。这就为用图线求解泰斯(Theis)方程奠定了基础,这种方法称为“配线法”。具体步骤:第一,根据井函数W(u)和u的值在双对数坐标纸上作曲线W(u)-![]() 标准曲线,也称“Theis曲线”,如图3.20所示;第二,在同样的双对数坐标纸上作s-t曲线,如图3.21所示,实际操作时,时间单位用min会更方便;第三,将绘有标准曲线的图3.20与绘有实测数据的图3.21重叠,保持坐标轴平行,移动图纸,使实测曲线与标准曲线重合;然后,选择配合点。配合点不一定要选在标准曲线上,任何一点均可。为方便计,常选W(u)=1和
标准曲线,也称“Theis曲线”,如图3.20所示;第二,在同样的双对数坐标纸上作s-t曲线,如图3.21所示,实际操作时,时间单位用min会更方便;第三,将绘有标准曲线的图3.20与绘有实测数据的图3.21重叠,保持坐标轴平行,移动图纸,使实测曲线与标准曲线重合;然后,选择配合点。配合点不一定要选在标准曲线上,任何一点均可。为方便计,常选W(u)=1和![]() =1的交点作为配合点,如图3.22所示。用大头针标定出配合点,在s-t曲线图纸上找出配合点对应的水位降深s和时间t,便得到一组值:W(u)=1、
=1的交点作为配合点,如图3.22所示。用大头针标定出配合点,在s-t曲线图纸上找出配合点对应的水位降深s和时间t,便得到一组值:W(u)=1、![]() =1、s和t。将时间t由min作单位换回以d作单位,代入式(3.41)中,就可求得导水系数T的值,再除以试验处的保水厚度,即得到渗透系数K。
=1、s和t。将时间t由min作单位换回以d作单位,代入式(3.41)中,就可求得导水系数T的值,再除以试验处的保水厚度,即得到渗透系数K。
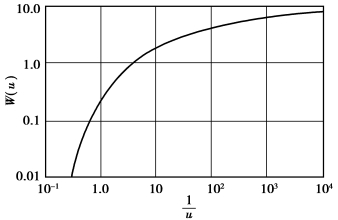
图3.20 W(u)- 标准曲线
标准曲线
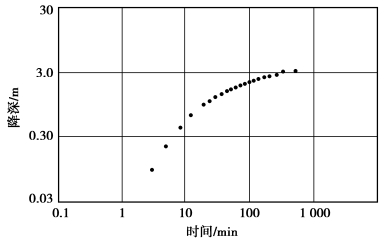
图3.21 实测的水位降深-时间关系s-t曲线
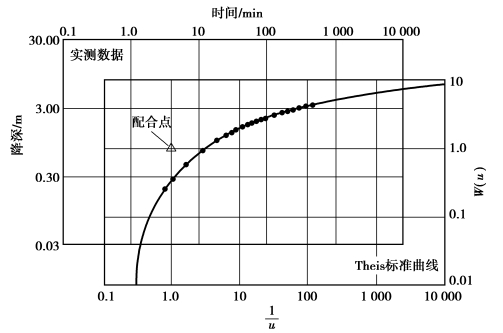
图3.22 实测s-t曲线与W(u)-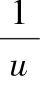 标准曲线配线
标准曲线配线
上述用s-t曲线与W(u)-![]() 标准曲线配线求水文地质参数的方法称为降深-时间配线法。当有多个观测孔时,还可按式(3.43)与(3.45)和式(3.43)与式(3.46)整理试验数据进行配线求水文地质参数,分别称为“降深-距离配线法”和“降深-时间距离配线法”。由于配线法的基础是在承压含水层的条件下求得的泰斯方程,所以上述配线法原则上适用于承压含水层。不过,如果对实测的水位降深作必要的校正,配线法依然可用于潜水含水层,作为一种近似,也可用于珊瑚岛。这是因为在潜水含水层中抽水会降低地下水位,减少含水层的饱水厚度,进而降低了含水层的导水系数,导致了比导水系数保持恒定时更大的观测降深。因此,在潜水含水层中进行抽水试验,用配线法求水文地质参数时,应对观测到的水位降深s进行校正,校正公式为:
标准曲线配线求水文地质参数的方法称为降深-时间配线法。当有多个观测孔时,还可按式(3.43)与(3.45)和式(3.43)与式(3.46)整理试验数据进行配线求水文地质参数,分别称为“降深-距离配线法”和“降深-时间距离配线法”。由于配线法的基础是在承压含水层的条件下求得的泰斯方程,所以上述配线法原则上适用于承压含水层。不过,如果对实测的水位降深作必要的校正,配线法依然可用于潜水含水层,作为一种近似,也可用于珊瑚岛。这是因为在潜水含水层中抽水会降低地下水位,减少含水层的饱水厚度,进而降低了含水层的导水系数,导致了比导水系数保持恒定时更大的观测降深。因此,在潜水含水层中进行抽水试验,用配线法求水文地质参数时,应对观测到的水位降深s进行校正,校正公式为:

式中,s′为校正后的水位降深,s为观测到的水位降深,b为试验开始时饱和含水层厚度。求得s′后,首先绘制s′和时间的对数曲线,应用上述配线法计算导水系数T,再除以试验处的饱和含水层厚度,即得到渗透系数K。在没有进一步的研究成果前,试验处的饱和含水层厚度可近似取为该处的淡水透镜体厚度。
此外,还可以用Bouwer和Rice提出的一种简便的非完整井试验确定潜水含水层渗透系数。这种试验属微水试验,在英语文献中称为“slug test”,图3.23是试验简图。试验时,瞬时(d t时段)从井中抽出或注入一定量的水,然后记录井中水位降深y(t)随时间t的变化,作lg y-t曲线,用以计算渗透系数K。这方法的理论依据为:井中水位突然下降或上升后,水位变化率d y(t)/d t与注入或抽出井中的流量Q(抽出为正,注入为负)间的关系可用下式表示:
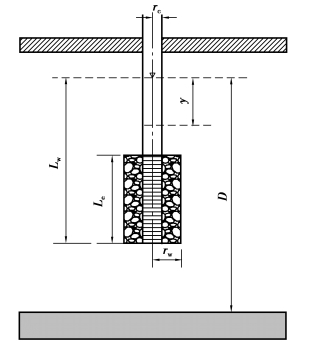
图3.23 Bouwer和Rice试验法简图

式中,y(t)为井中水位降深;rc为井半径。由稳定流公式,流量Q可表示为:

式中,K为渗透系数,Le为井过滤器长度,Re为影响半径,rw为井或过滤器半径。将式(3.49)代入式(3.48)中,令t=0时(停止抽水或注水),y=y0,可解得渗透系数的表达式:
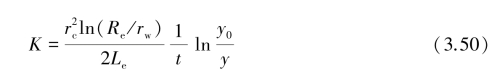
式中,ln(Re/Rw)由经验方程求得:
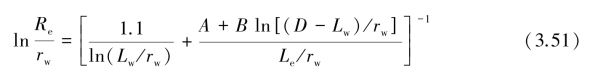
式中,Lw为井底至潜水面之间的距离;A与B由Le/rw的比值用图3.24确定;D是含水层厚度,在珊瑚岛抽水试验中可取为淡水透镜体的厚度。如果在大陆上,用完整井进行试验,Lw=D,那么式(3.51)简化为:
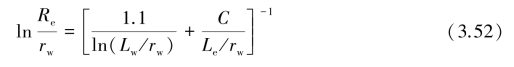
式中,C亦由Le/rw的比值用图3.24确定。
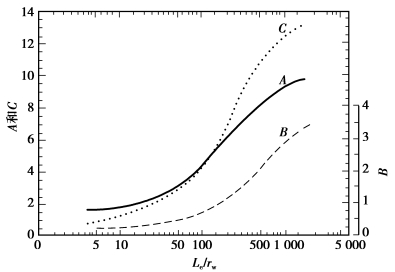
图3.24 无量纲参数A、B、C与Le/rw的关系
Bouwer和Rice法处理数据的步骤如下(Lw≠D):
①在半对数坐标纸上绘制lg y-t曲线;
②用直线拟合该曲线的线性部分,延长直线至t=0,得到y0;
③计算ln[(D-Lw)/rw],如果ln[(D-Lw)/rw]>6,则取ln[(D-Lw)/rw]=6;
④在图3.24中查得A、B值;
⑤计算ln(Re/rw);
⑥在直线上任找一点,记下该点的y、t值,连同y0代入式(3.50)中,计算渗透系数K。
如果过滤器长度Le超过过滤器半径rw的8倍(Le/rw>8),可用下式计算渗透系数:

式中,t0.37为水位上升或下降至水位初始变化量37%时的时间,如图3.25所示。
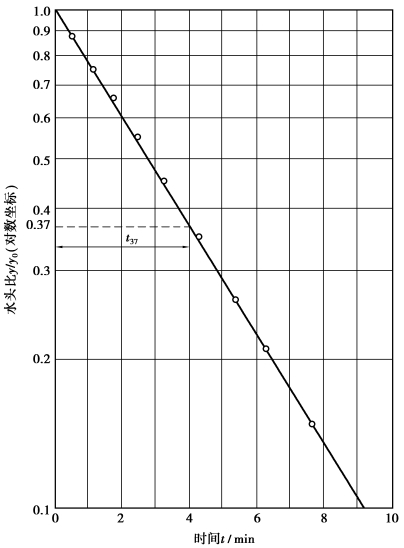
图3.25 降深比y/y0与时间t的关系示意曲线
为说明这种微水试验方法的应用,Bouwer和Rice给出了一个例子:试验用井位于以一冲积沉积层内,潜水面埋深3 m,含水层厚D为80 m,潜水面至井底的距离Lw为5.5 m,过滤器长Le为4.56 m,井半径rc为0.076 m,过滤器半径rw取为0.12 m。试验时将一Statham PM131TC型压力传感器置于水面下1 m深处,再将一圆柱体放于水面下,水面抬升0.32 m。当水面恢复至平衡位置时,取出圆柱和压力传感器。由压力传感器记录的压力(水头)随时间变化的数据,在半对数坐标纸上绘制如图3.26的曲线,延长线上的直线部分,上端与y轴(t=0)相交,得到y0=0.29 m,非常接近水面抬升值0.32 m;在下端延长线上,任取一时间t=20 s的点,其对应的y=0.002 5 m。于是:


图3.26 微水试验y-t图
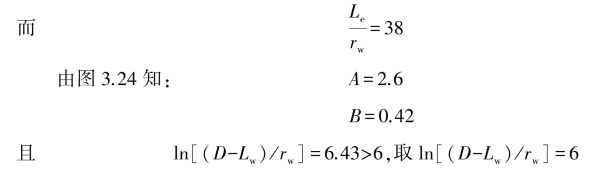
将上述各有关值代入式(3.51)中,即
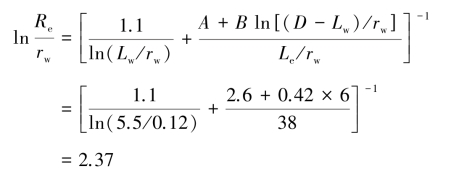
由式(3.50)得:
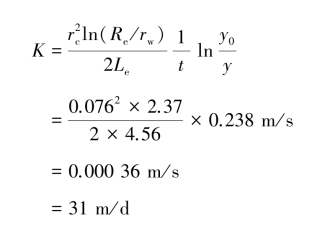
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




