水文地质参数分析及应用

珊瑚岛的地质结构对赋存于其中的淡水透镜体的水质、水量和动力学特性均有重要影响，这种影响可以通过水文地质参数来表达。淡水透镜体属于潜水水体，相关的重要水文地质参数包括孔隙率、渗透系数、给水度和弥散系数。

（1）孔隙率

在珊瑚岛双含水层地质结构中，不整合面以上的全新世含水层由珊瑚等生物碎屑颗粒堆积而成，处于未固结或弱固结状态，颗粒与颗粒之间形成孔隙；不整合面以下的更新世含水层虽已岩化成生物灰岩，但由于原生礁固有的孔隙和侵蚀、溶蚀，以及一些海洋生物的钻掘作用，岩体也“千疮百孔”。因此，整个珊瑚岛含水层是一多孔的介质含水体系。这一体系中包含有固相、液相和气相，其中，固相是指生物颗粒和包含孔隙溶洞的珊瑚灰岩，在水文地质学上称为“多孔介质”，也称“骨架”；液相是指上层淡水和下层咸水；气相指潜水面以上多孔介质中的气体。

多孔介质最一般的特征是包含大量孔隙，孔隙的大小、形状和分布各不相同，许多孔隙相连形成通道。珊瑚岛礁淡水透镜体便赋存于这些孔隙之中，透镜体淡水在孔隙通道中流动。因此，多孔介质中具有的孔隙在珊瑚岛水文地质研究中有重要意义。工程上把多孔介质孔隙具有的这种大小、形状、分布和连通各异的性质统称“孔隙性”，表征多孔介质孔隙性的常用参数称为“孔隙率”，用n表示。孔隙率的定义是多孔介质中的孔隙体积uv与多孔介质总体积u之比，即

式中，us是固相体积，u＝uv＋us，孔隙率n是无量纲参数。如果uv为多孔介质中全部孔隙体积，这样定义的孔隙率称为“总孔隙率”。在多孔介质的全部孔隙中，有一部分孔隙具有一个死端，只能容纳流体，不能让流体通过，这样的孔隙称为“死端孔隙”。此外，即使能通过流体的孔隙通道，由于介质颗粒表面吸附一薄层（如厚度小于0.5μm）不动的结合水，也会减少透过流体的孔隙体积。在淡水透镜体动力学的研究中，只有能通过流体的孔隙才有意义，称之为“有效孔隙”，其体积用ue表示，仿照式（2.1），可以定义有效孔隙率ne，即

本书以后的章节中，除非特别说明，孔隙率均指有效孔隙率。

影响孔隙率的因素很多。它的大小与颗粒粒径分布、孔径分布有关，也与颗粒形状、排列以及多孔介质中的胶结物质、沉积环境有关。在颗粒粒径相同的理想条件下，球形颗粒若按图2.3（a）的方式排列，即每个球形颗粒均在下层球体的顶端，这种模式构成的多孔介质的孔隙率为47.65%；如球形颗粒按图2.3（b）的方式排列，即每个球形颗粒堆放在下层相邻四个球体的中心位置，则这种模式构成的多孔介质的孔隙率为25.95%。

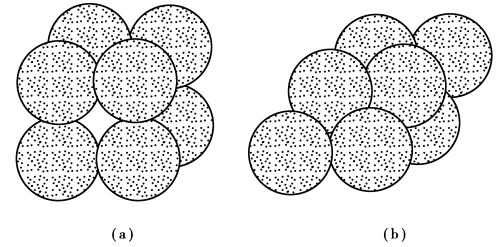
图2.3　相同直径球形颗粒的两种排列

上述两种情况下的孔隙率都与球形颗粒的直径无关，仅取决于排列。由此可以推断，珊瑚等生物碎屑在沉积过程中，如果分选程度较好，具有大致相同的粒径，可近似为圆球，那么由排列方式决定的孔隙率应为26%～48%。自然界中的岩土类多孔介质，颗粒并非标准圆球，也非相同粒径的颗粒沉积在一起，而是大小不同、形状各异的颗粒混合在一起，特别当小颗粒填充在大颗粒之间的孔隙中时，就会对孔隙率带来显著的影响。另外压缩和胶结程度对孔隙率也有影响。因此，岩土类多孔介质的孔隙率与按相同直径球形颗粒排列推算出来的孔隙率相比会有差异。自然界中典型岩土类多孔介质的孔隙率见表2.1。表中部分不同颗粒对应的粒径见表2.2。

表2.1　典型岩土类多孔介质的孔隙率

注*：表示样本受到扰动，其余为未受扰动的样本。

表2.2　岩土类多孔介质颗粒对应的粒径

讨论珊瑚岛含水层多孔介质的孔隙率时，还需要联系其双含水层地质结构。在不整合面之上，是松散沉积物，孔隙率取决于颗粒大小与级配；不整合面之下是岩化较好的珊瑚灰岩，孔隙率依赖于原生孔隙结构、胶结与溶蚀。在地质上，纹理粗糙的卵石和碎石、多孔隙珊瑚礁灰岩和溶蚀产生大量次生孔隙的岩层，均有很高的孔隙率；而在细密纹理和分选性差的沉积物以及弱胶结的多孔介质中，孔隙率较低。因此，珊瑚岛不整合面之下更新世灰岩的孔隙率大于其上全新世沉积层的孔隙率。珊瑚岛大多分布在热带海域，由珊瑚和其他造礁生物营造而成，有相同的地质构造，因而有相近的孔隙率，如在太平洋，在马绍尔群岛Majuro环礁的Lautra岛上，全新世含水层的孔隙率为0.20，更新世珊瑚灰岩的孔隙率为0.30；美国福罗里达州的St.George岛，全新世含水层的孔隙率为0.35；南太平洋新喀里多尼亚的Mba岛，全新世含沉积层的孔隙率为0.10～0.30，更新世珊瑚灰岩的孔隙率为0.10～0.50；在印度洋，在Cocos（Keeling）群岛的Home岛上，全新世含水层的孔隙率为0.30。可见，淡水透镜体赋存的全新世含水层，孔隙率一般为0.30～0.40。一些学者研究淡水透镜体的动力学特性时，用的孔隙率也在这一区间取值：Adrian D.Werner等实验研究倒锥特性时，取孔隙率为0.38；H.-J.Diersch等研究弥散对倒锥影响时，取孔隙率为0.36。不过也应该指出，由于珊瑚岛与主导风相对位置的不同、沉积过程中胶结程度的不同，不同珊瑚岛的孔隙率会有差异，当要准确研究淡水透镜体的动力学特性时，需要在岛上进行实地勘测，或者实验测量，也可以在模拟过程中对参数进行校准，以确定岛屿地层的孔隙率。

由于多孔介质的压缩性，多孔介质受力时会产生变形，引起孔隙率变化。在饱和状态下，某一深度处多孔介质承受的力可分为内力和外力。内力由流体静压p产生，外力由该处地层之上的覆盖层施加，设对应的应力为σ。在这两种力作用下，多孔介质呈现压缩变形。由于饱和多孔介质中，介质受力的变化主要由水头变化产生的静压p的变化引起，外力对应的σ一般保持不变，因此，通常考虑由静压p变化引起的多孔介质的压缩变化。多孔介质的这种压缩变化或压缩性可用压缩系数表示，定义单位静压变化引起的介质骨架体积us和孔隙体积uv的相对变化率分别为骨架压缩系数αs和孔隙压缩系数αv：

类似地，多孔介质的压缩系数α定义为：

因为，u＝uv＋us

所以

由孔隙率n的定义式（2.1）得：

将式（2.6）代入式（2.5）得：

再由式（2.7）和式（2.8）得：

将式（2.10）和式（2.11）代入式（2.9），并由式（2.3）和式（2.4），得：

在珊瑚碎屑生物沙砾沉积物等岩土类多孔介质中，介质骨架的压缩性远小于孔隙的压缩性，即

于是近似有：

多孔介质的压缩性会对多孔介质地下水的贮存或释放量带来影响。

（2）渗透系数

渗透系数（coefficient of permeability）是包括珊瑚沙砾在内的岩土类多孔介质在一定水力梯度作用下，透过流体即地下水能力的一种量度，一些文献和著作也称其为“水力传导系数（hydraulic conductivity）”，用K表示，具有速度的量纲，常用单位为m/d。渗透系数表征了岩土介质流过流体的力学性能，因此，其大小既取决于流体的性质，也与介质骨架有关。介质骨架性质包括介质颗粒大小与岩土基质结构，如孔隙形状、大小、分布、比表面积、弯曲率和孔隙率等。流体性质主要包括流体密度、动力黏性系数。因此，渗透系数K可由介质及流体两方面的性质确定：

式中，ρ为流体密度，g为重力加速度，μ为流体动力黏性系数，ν为流体运动黏性系数，ki为介质固有渗透率（intrinsic permeability），简称“渗透率”。

流体密度、黏性系数表征了流体的性质。渗透率ki表征了介质骨架的性质，具有长度平方的量纲［L2］，常用单位为cm2。沉积物颗粒越小，颗粒表面与地下水的接触面越大，水流动时受到的阻力便越大，使渗透率下降；而对于分选性良好的沉积物，渗透率与颗粒大小成正比。渗透率ki可用下式表示：

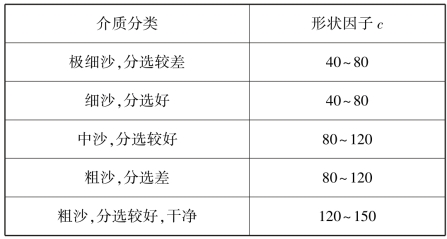
式中，比例系数c称为形状因子，是一个与多孔介质特性（如松散岩土颗粒大小和分布、颗粒球度、级配以及填充度和密实度）有关的无量纲参数，取值为45～140，小值适用于黏土介质，大值适用于沙砾介质，常用平均值为100。也有学者建议c值按不同介质选取，见表2.3。d10为颗粒有效直径，单位为cm，d10的含义是小于该直径的颗粒质量占多孔介质总质量的10%。

表2.3　不同介质的c值

渗透率ki的计算，还有种种其他方法，J.贝尔曾作过较系统的归纳，他的方法大致分为三类。

第一类为纯经验公式，即

式中，d为多孔介质颗粒平均粒径，单位为μm；ki单位为cm2，该公式由试验结果拟合而来。另一个公式是从量纲分析结合实验得来的Fair-Hatch公式，即

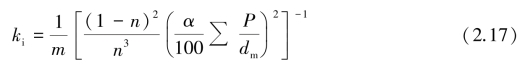
式中，m为排列因子，试验值为5；n为孔隙率；α为介质颗粒的形状系数，其值为6.0～7.7，圆球颗粒取6.0，棱角状颗粒取7.7；P为对介质颗粒进行筛分时相邻筛子之间所包含的颗粒质量百分数；dm为相邻筛孔大小的几何平均值。

第二类为纯理论公式，其中比较著名的有Kozeny方程：

式中，c0是Kozeny系数，根据流体流经多孔介质孔隙时过流断面的形状取值：圆形断面c0取0.5，正方形断面c0取0.562，等边三角形断面c0取0.597，长条形断面c0取0.667。M为比表面积。

第三类为半经验公式。由于Kozeny方程中c0的值难以确定，为避免这一困难，引入多孔介质固体骨架的比表面积Ms，由Kozeny方程可导得另一关系式，称为Kozeny-Carman方程，即：

(www.xing528.com)

式中，c0为一个由实验确定的经验系数。因此，Kozeny-Carman方程为半经验公式。Carman建议公式中的c0取0.2，该值与实验吻合最好。骨架的比表面积Ms由下式定义：

式中，As为多孔介质体积u中所有颗粒的总表面积，us为u中介质的固相体积。式（2.18）中的M与Ms之间的关系为M＝（1-n）Ms。

上面介绍的渗透率ki的计算方法为确定多孔介质的渗透系数K提供了几种途径。应该指出，当使用经验或半经验公式计算渗透率ki时，需要通过实验确定公式中系数的数值；而用理论公式计算ki时，又因实际的孔隙通道断面不具备标准的几何外形，使c0这一Kozeny系数的取值困难。在实际应用中，常采用实验的方法直接测得多孔介质的渗透系数K。不过要注意，由于天然岩土类多孔介质组分及结构千差万别，即使同一种介质，取自不同地方的样品，测得的渗透系数也会有很大差别，有的会相差几个数量级。因此，大多文献资料在列出多孔介质的渗透系数时给出的是取值范围，见表2.4。

表2.4　不同岩土类多孔介质的渗透系数取值范围

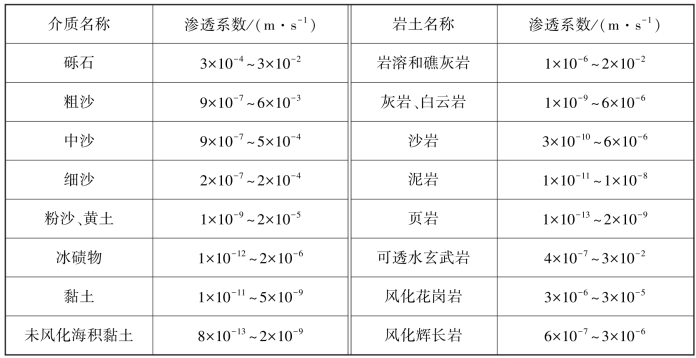
在珊瑚岛的含水层中，尽管介质同为珊瑚生物碎屑，但其渗透系数依然呈现出较大的差别，尤其珊瑚岛是双含水层结构，不整合面上下地质单元中的渗透系数差别更为显著。如东印度洋的Cocos（Keeling）群岛，通过现场降水头和常水头方法测试，在全新世沉积层中，渗透系数为3～12 m/d，而在不整合面之下更新世石灰岩层中，渗透率急剧增加，渗透系数高达30～500 m/d，一些测值甚至高达1 000 m/d；印度洋中部的迪科加西亚环礁岛上，通过抽水实验获得的渗透系数为3～300 m/d不等，有2个量级的差别，中值为61 m/d，高值在岛屿向海一侧，对应了粗颗粒的砾石，低值在潟湖一侧，对应了细碎的沙粒和淤泥；珊瑚岛含水层的渗透系数还和岛屿在环礁礁盘上相对于主导风的位置有关。R.T.Bailey等在进行太平洋和印度洋环礁岛屿水文地质模拟时，迎风岛和背风岛全新世含水层的渗透系数分别取400 m/d和50 m/d进行数值计算，得到的透镜体厚度值与观测值吻合很好。

（3）给水度

饱和含水层中，水赋存于介质孔隙中，一部分水在重力作用下能在孔隙通道中流动，并可排出饱和介质外，这部分水称为“重力水”，是地下取水的来源。为表征饱和含水介质在重力作用下排出水的能力，引入“给水度”的概念。给水度Sy（specific yield）是指饱和含水介质在重力作用下能排出水的体积uw与饱和含水介质体积u之比，即

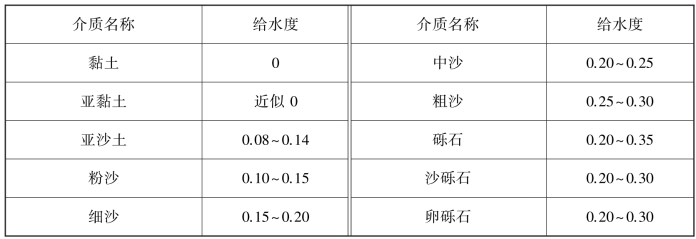
给水度与介质孔隙率和颗粒大小有关。由于岩土介质颗粒表面带有电荷，水分子是极性分子，在静电引力作用下，孔隙中紧贴颗粒的一薄层水分子便吸附于颗粒表面而成为结合水，粒径越大，比表面积越小，结合水的含量也越小；相反，粒径越小，比表面积越大，结合水的含量也越多。结合水受到固体表面的强烈吸引，不能在重力作用下流动，因此，当重力水从保水介质中流出时，结合水仍然留存在介质内。这样，孔隙率相同的两种介质，小颗粒介质的结合水多，能在重力作用下流出的水就少，因而给水度小，而大颗粒介质的给水度则大。表2.5列出了一些学者提供的岩土多孔介质的给水度。表2.6列出了另一些学者推荐的松散沉积物给水度的经验值。

表2.5　常见岩土介质的给水度

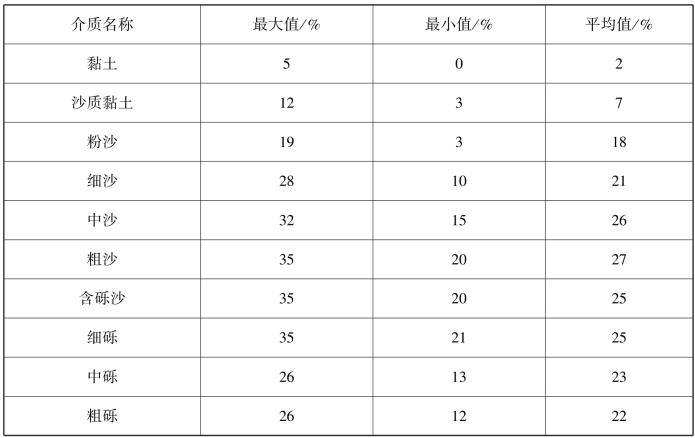
表2.6　松散沉积物给水度的经验值

饱和含水多孔介质中的结合水虽不能在孔隙中自由流动，但与颗粒表面稍远、结合较弱的结合水可以被植物根系吸收。

设体积为u的饱和含水介质中结合水的体积为uτ，uτ与u之比定义为持水度Sτ：

持水度与颗粒大小的关系正好和给水度与颗粒大小的关系相反，小颗粒介质持水度大，大颗粒介质持水度小，见表2.7。

表2.7　不同粒径颗粒介质的持水度

持水度与给水度之有一定关系，两者之和等于孔隙率n：

由上式可知，当持水度Sτ很小可以忽略不计时，给水度Sy近似等于孔隙率n。

（4）弥散系数

流体在多孔介质中流动时，流体中的含有物（如溶质），一方面随主流在流动方向上传输，另一方面会向四周迁移扩展，这种溶质的迁移扩展现象称为“弥散”。从运动观点看，弥散源于分子扩散和流速分布不均。分子扩散由无规则热运动引起，从溶质浓度高的地方向浓度低的地方迁移，受浓度梯度影响，扩散通量q服从Fick定律：

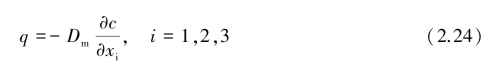
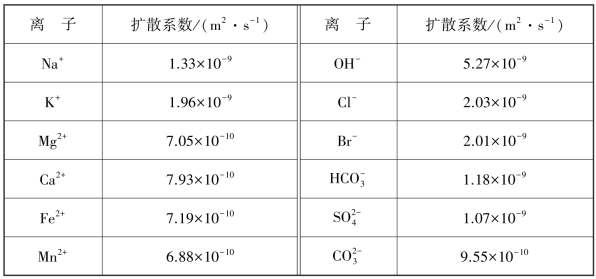
式中，q是单位时间内通过与xi轴垂直的单位面积的溶质质量（M·L-2·T-1），i＝1，2，3，xi轴分别对应于x、y、z轴；Dm为分子扩散系数（L2·T-1）；c为溶质浓度（M/L3）；负号表示溶质扩散方向与浓度梯度方向相反。分子扩散系数的值随溶质、流体种类和温度而变化，25℃时水中几种离子的扩散系数见表2.8：

表2.8　25℃时水中离子的扩散系数Dm

然而，在多孔介质中，溶质的扩散远没有在敞开水体中那么容易，因为扩散只能发生在孔隙流体中，所以溶质必须围绕介质颗粒运动，在相同位移时溶质经过的流程更长。因此，在多孔介质中，扩散进程比敞开水体中缓慢，但扩散仍遵从Fick定律。为反映多孔介质对扩散的弱化影响，引入“有效扩散系数”D*替代式（2.24）中的Dm。有效扩散系数D*与分子扩散系数Dm之间有以下关系：

式中，τ是一个与孔隙通道弯曲度有关的系数，由于量测弯曲度非常困难，τ实际上是一个经验值，可通过扩散实验获得。用地质材料在实验室内进行试验，得到τ的取值范围为0.01～0.5。有学者指出，对黏土，τ取0.1；对沙，τ可取0.7。

流体在多孔介质中流动时流速分布不均由多种原因引起。在多孔介质中，孔隙大小不同，相互连接而成的通道蜿蜒曲折，彼此连通，岩土多孔介质孔隙结构和地下水流示意图如图2.4所示。其中，图（a）为孔隙中的速度分布，图（b）为孔隙通道中的流程变化。由图可知，地下水在孔隙中流动，孔隙中心部分流速大，边缘部分流速小；大孔隙内流速大，小孔隙内因黏性影响流速小；特别地，由于孔隙大小和连通形式千差万别，流体在孔隙通道中流动时流程会发生弯曲、分叉与汇合。这就使得多孔介质中尽管主流沿着一个方向运动，但是各点流速的大小和方向都不尽相同，即各点速度与主流断面平均速度存在差异，每个流体质点按照孔隙中流速分布迂回曲折前进，经历一系列流速变化，不同的流体质点会经历不同的流动序列，导致了溶质在沿主流方向运移的同时还向四周散布扩展，占据多孔介质中越来越大的范围，这就是“弥散”。在流动方向上由于流速大小差异产生的弥散，称为“纵向弥散”；而在垂直于主流的方向上由于分叉流动产生的弥散，称为“横向弥散”。横向弥散，也可认为是介质孔隙中流动在垂直于主流方向上具有速度分量而产生的弥散。多孔介质中，这种由于速度方向和大小与平均流速不同而产生的弥散，称为“机械弥散”。

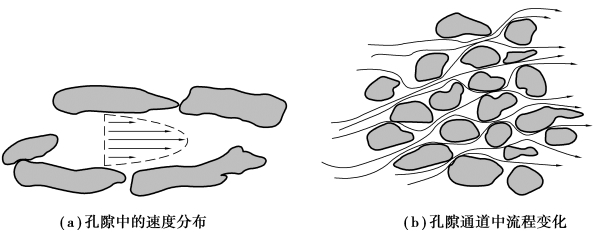
图2.4　岩土多孔介质孔隙结构和地下水流

比拟分子扩散，机械弥散产生的弥散通量与浓度梯度成正比，也可用Fick定律描述。考虑一均匀地下水流，取x轴与地下水流方向一致，则弥散发生在纵向和横向两个方向。设x、y、z三个方向上的弥散通量分别为Jx、Jy和Jz，由Fick定律：

式中，Jx、Jy、Jz分别为单位时间内由于弥散迁移而通过垂直于x、y、z轴单位面积的溶质的质量（M·L-2·T-1）；Dx、Dy、Dz分别为x、y、z方向上的机械弥散系数（L2·T-1）；c为溶质浓度（M·L-3）；负号表示弥散方向与浓度梯度方向相反。由于弥散是介质孔隙中流体质点速度与主流断面平均流速差异的累计结果造成的，随着地下水流速度的增大，这种累计差异也增大，弥散迁移作用增强。因此，有理由认为，弥散通量与平均流速成正比。如果这种正比关系通过弥散系数来反映，那么Dx、Dy、Dz可表示为：

式中，比例系数αL称为纵向机械弥散度（L），描述水流方向上的弥散迁移，与多孔介质的性质有关；αT为横向机械弥散度（L），描述垂直于水流方向上的弥散迁移，也与多孔介质的性质有关；v为孔隙中平均渗流速度（L·T-1）。

在地下水的流动过程中，分子扩散和机械弥散是混合在一起的，难以区分开来，因此，实际应用中通常把两者结合在一起考虑，定义一个水动力弥散系数来反映两者的作用：

式中，DL称为纵向弥散系数，反映平行于水流方向的水动力弥散；DT称为横向水动力弥散系数，反映垂直于水流方向的水动力弥散。如果考虑分子扩散，式（2.30）、式（2.31）中的Dy、Dz应为横向水动力弥散系数，即Dy＝Dz＝DT。在实际的地下水流动中，绝大多数情况下，与机械弥散相比，分子扩散作用微弱，可以忽略。

水动力弥散系数的值主要通过实验室试验和现场试验获得。Perkins和Jonhson利用填沙圆筒和示踪剂在实验室进行了大量试验，并参考其他研究者的结果，得到了无量纲水动力弥散系数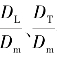与Peclet数Pe＝的关系曲线，如图2.5所示。

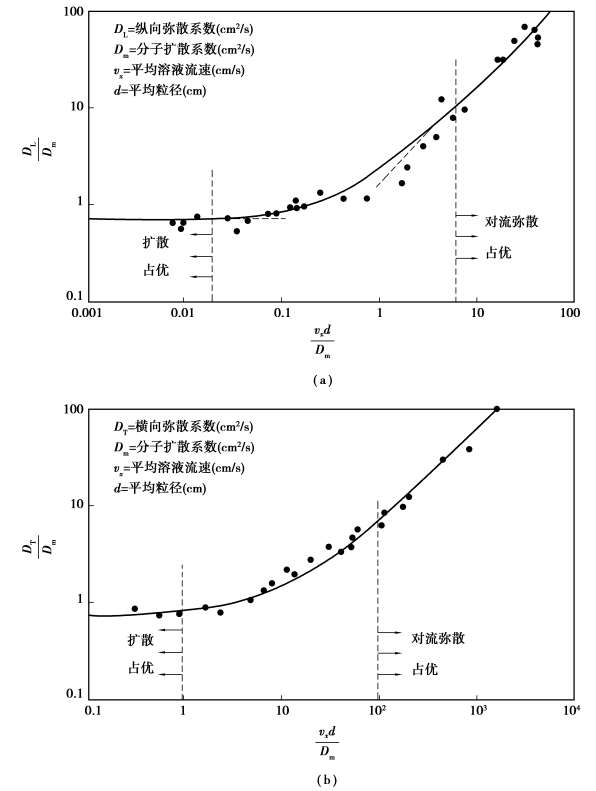
图2.5　无量纲水动力弥散系数与Pe的关系图

现场试验通常采用单井或双井，将含有恒定浓度示踪剂的水通过水井注入含水层，然后再从井中抽水，把含有示踪剂的水从地下抽出，由示踪剂浓度的变化计算弥散度。需要指出的是：弥散度的测量受观测尺度的影响。在实验中发现，随着示踪剂锋面迁移距离的增加，即锋面流程越长，测得的纵向弥散度αL越大，如图2.6所示。从图2.6中可以看到，纵向弥散度αL约为流程长度的1/10。纵向弥散度αL随着观测尺度增大而增大的现象，称为“弥散的尺度效应”。具有这种效应的纵向弥散度αL，即现场流程尺度条件下的纵向弥散度称为“宏观弥散度”，亦称“表观弥散度”，记为αm。产生尺度效应的原因，主要是随着流动距离的增大，介质孔隙结构和渗透系数发生变化的可能性增大，孔隙中流速与介质断面平均流速的差异增加，导致机械弥散度增大。这从实验室试验和现场测试的结果也可看出，实验室试验给出纵向弥散度一般为0.01～1 cm，而野外现场观测到的纵向弥散度会较之大2～4个量级。不过，纵向弥散度也并非随观测尺度的增大持续增加，当流动路径变得足够大时，流体质点就可能碰到所有可能发生的变化，机械弥散度会趋近一个最大极限值。

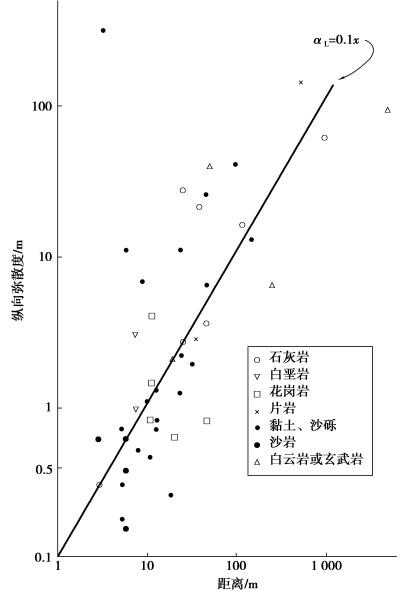
图2.6　纵向弥散度现场测值随测量尺度的变化

表观弥散度αm仍可通过试验确定。Xu和Eckstein收集了大量的数据，进行回归分析，得到一非线性关系式为：

式中　αm——表观弥散度，m；

　　　Ls——扩散质流经的距离，也就是源与测量点的距离，m。

用上式计算可以发现，随着现场尺度的增大，表观弥散度增大的速率减小，大于几千米后，表观弥散度随距离的变化很小。

横向弥散度αT的值可由与纵向弥散度αL的比值来计算。由于溶质主要在地下水主流方向上而非在垂直于流动的横向上迁移扩展，所以通常观察到的横向弥散度比纵向弥散度小，并且横向弥散度也受观测尺度的影响。根据一些现场实测数据，的比值为6～20。有的学者把横向弥散度再分为横向水平弥散度αTH和横向垂直弥散度αTV，而且认为横向水平弥散度αTH一般比纵向弥散度αL低一个数量级，横向垂直弥散度αTV又比横向水平弥散度αTH低一个数量级。