逐点比较法直线插补原理详解

以第一象限的线段为例，如图1-12所示，线段OA为待加工零件的一段轮廓，起点为坐标原点，终点A的坐标为A（x_e，y_e），P（x_i，y_i）为加工过程中刀具的轨迹点。若P点在OA上，则P点的坐标满足该线段的方程，即

改写为y_ix_e-x_iy_e=0

由此定义直线插补的偏差判别式为：

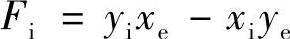
（1）偏差判别

1）若P点位于线段OA上，则有F_i=0。

图1-12 逐点比较法直线插补原理

2）若P点位于线段OA上方，则有F_i＞0。

3）若P点位于线段OA下方，则有F_i＜0。

（2）坐标进给 坐标进给的方向是使偏差缩小的方向。根据这个原则，当F_i＞0时，向+X轴方向进给一步，使点P接近直线OA；当F_i＜0时，向+Y轴方向进给一步，使点P接近直线OA；当F_i=0时，可向+X轴方向进给一步，也可向+Y轴方向进给一步，但通常约定向+X轴方向进给一步，因此将F_i＞0与F_i=0归为一类。

（3）新偏差计算 通常采用递推公式进行插补运算的新偏差计算，即设法找出相邻两个轨迹点偏差值之间的关系，每进给一步后，新轨迹点的偏差可通过前一轨迹点的偏差推算出来。由于起点是给定直线上的点，即F₀=0，因此，所有其他轨迹点的偏差都可以从起点开始一步一步推算出来。(www.xing528.com)

当F_i≥0时，轨迹点向+X轴方向进给一步，P点的坐标变为（x_i+1，y_i+1），新偏差为

因为

所以 F_i+1=F_i-y_e

当F_i＜0时，轨迹点向+Y轴方向进给一步，同理

综上所述，加工第一象限的线段时，偏差函数与进给方向的对应关系如下：当F_i≥0时，向+X轴方向进给一步，新偏差为F_i+1=F_i-y_e；当F_i＜0时，向+Y轴方向进给一步，新偏差为F_i+1=F_i+x_e。

（4）终点判别 在轨迹点向某一个方向进给一步后，需要进行终点判别，若已经到达终点，就停止插补运算，否则返回，继续进行插补运算和偏差判别。终点判别有以下三种方法：

1）总步长法。以两个坐标轴方向位移的总步数作为计数值，每插补一次，就从总步数中减1，当总步数减到0时表示已到达终点。

2）投影法。以投影长度较大的坐标值作为终点判别计数值，在插补过程中，该坐标轴方向每进给一步，就将计数值减1，减到0时表示已到达终点。

3）终点坐标法。以目标点两个坐标轴方向的坐标值分别作为计数单元，在插补过程中，向+X轴方向进给一步，则X向的计数值减1，向+Y轴方向进给一步，则Y向的计数值减1，当两者均减到0时，才表示到达终点位置。