直线位置判别法则：相交、平行、交叉

两直线的相对位置有三种情况：相交、平行、交叉。

1.两直线平行

空间两直线平行，它们的同名投影一定平行；反之，两直线的各同名投影平行，则两直线在空间必然平行，如图2-18所示。

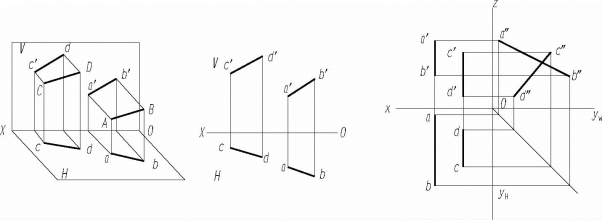
图2-18　两直线的相对位置

2.两直线相交

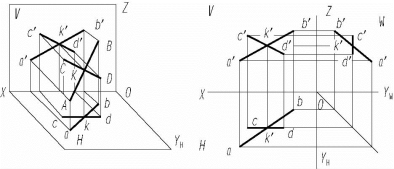
空间相交两直线，其同面投影均相交，且交点符合点的投影规律。若两直线的同面投影均相交，其交点同属于两直线，则它们在空间也一定是相交的；反之交点不符合点的投影规律，则两直线不相交，如图2-19所示。

(www.xing528.com)

图2-19　相交两直线的投影

3.两直线交叉

两直线既不平行又不相交，称为交叉直线。

若空间两直线交叉，则它们的同名投影不同时平行，或者它们的各同面投影虽然相交，但其交点不符合点的投影规律；反之亦然，如图2-20所示。

4.判定空间交叉两直线的相对位置

空间交叉两直线的投影交点，不是真交点，实际上是空间两点的投影重合点。利用重影点和可见性，可以很方便地判别两直线在空间的位置。如图2-20（b）所示，当判断直线ABCD 的正面重影点m′（n′）的可见性时，由于M，N 两点的水平投影m 比n 的Y 坐标值大，所以当从前往后看时，点M 可见，点N 不可见，由此可判定直线CD 在前方。同理，从上往下看时，点E 可见，点F 不可见，可判定直线CD 在直线EF 的上方。

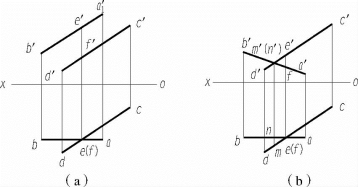
图2-20　两直线交叉