点的水平和侧面投影相等，反映Y坐标值

1.点的三面投影

首先建立三个互相垂直的投影面V、H 及W，其间有一个空间点A，它向投影平面H 投影后得投影点a，向V 面投影后得投影点a′，向投影平面W 投影后得投影点a″，投射线Aa 及Aa′是一对相交线，且垂直于X 轴，故处于同一平面内，如图2-10（a）所示。

移去空间点A，保持V 面不动，将H 面绕OX 轴向下旋转90°，W 面绕OZ 轴向右旋转90°，H、W 面与V 面处于同一平面，即得到点A 的三面投影图，如图2-10所示。图中OY 轴被假想分为两条，随H 面旋转的称为OYH 轴，随W 面旋转的称为OYW 轴。如图2-10（b）、（c）所示。

图2-10　点的三面投影

规定把空间点用大写字母A、B、C 等标记，它们在H 面上的投影用相应的小写字母（如a、b、c）等标记，在V 面上的投影用相应的小写字母在右上角加一撇（如a′、b′、c′等）标记，在W 面上的投影则加两撇（如a″、b″、c″等）标记。

将三投影面展开后即得到平面内的投影如图2-10所示，两投射线aa′，a′a″称为投影连线，分别垂直于X 轴和Z 轴。只要知道A（x，y，z）的坐标值，沿轴量取坐标，过该点画该坐标轴的垂线即投影连线，两投影连线的相交点即投影点a、a′、a″。

2.点的三面投影图规律

①点的正面投影与水平投影的连线垂直于OX 轴（aa′⊥OX）。

②点的侧面投影与正面投影的连线垂直于OZ 轴（a′a″⊥OZ）。

③点的水平投影a 到OX 轴的距离和侧面投影a″到OZ 轴的距离相等，均等于点A到V 面的距离，都反映Y 坐标值。

熟悉点的三面投影规律后，根据点的两面投影，可以求出该点的第三面投影，如图2-11所示。

【例2-1】作点A（30，20，12）的三面投影。

【解】沿X 轴量30，作X 轴的投影连线（垂线⊥X），沿Y 轴量20，作Y 轴的投影连线（垂线⊥Y），两投影连线交于点a；沿Z 轴量12，作Z 轴的投影连线（垂线⊥Z），两投影连线交于点a′，与YH 投影连线交于点a″（做法如图2-12所示）。

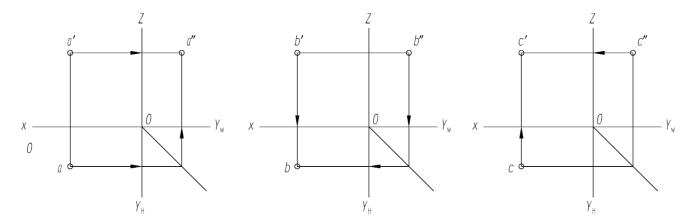
图2-11　求点的第三面投影

图2-12　点的三面投影

3.特殊位置点的投影(www.xing528.com)

当某点的某一坐标值为0时，该点投影就处于投影面上；当某点的两个坐标值为0时，该点投影就处于投影轴上；当某点的三个坐标值等于0时，该点投影就处于坐标原点上。

（1）在投影面上的点

如图2-13所示，A（50，0，35）、B（30，12，0）、C（0，20，20）三点分别处于V 面、H 面及W 面上，由此得出投影面上的点的投影性质为：①点的一个投影与空间点本身重合；②点的另外两个投影分别处于不同的投影轴上。

图2-13　特殊点的三面投影

（2）在投影轴上的点

D（0，30，0）点投影如图2-13所示，点D 和它的水平投影、侧面投影重合于OY 轴上，点D 的正面投影d′位于原点。

4.两点间的相对位置及重影点

（1）两点相对位置的确定

立体上两点间的相对位置，是指在三面投影体系中，一个点处于另一个点的上、下、左、右、前、后的方位。两点相对位置可用坐标值的大小来判断，Z 方向坐标值大者在上，反之在下；Y 方向坐标值大者在前，反之在后；X 方向坐标值大者在左，反之在右。如图2-14所示，A、C 两点的相对位置为zA ＞zC，因此点A 在点C 之上；yA ＞yC，点A在点C 之前；xA ＜xC，点A 在点C 之右，结果是点A 在点C 之右、前、上方。

图2-14　点在空间的相对位置

（2）重影点

当空间两点的某两个坐标相同，即当两点位于同一条投射线上时，它们在该投射线垂直的投影面上的投影重合于一点，此空间两点称为对该投影面的重影点。

如图2-15所示，C、D 两点位于垂直于H 面的同一条射线上（xC ＝xD，yC ＝yD），水平面投影c 和d 重合于一点。

由正面投影（或侧面投影）可知zC＞zD，即C 点在D 点的上方。因此点D 的水平投影d 被点C 的水平投影c 遮挡，是不可见的，规定标记时在d 上加圆括号以示区别。

图2-15　重影点的投影