Schaeffler相组分图优化方案

Anton Schaeffler^[19]认识到前面的研究结果只要和焊接结合就可以得到实用。他认为Strauss-Maurear相组分图为预测铬-镍合金钢板的微观组织提供了蓝图，而Newell-Fleischman^[13]和Field^[14]的关系式几乎可以直接用于焊接。他的研究就集中于把这些结果组合起来形成一个焊缝金属的相组分图，用它可以由焊缝的成分来预测其微观组织。他提出的相组分图包含了作为坐标轴的铬当量和镍当量关系式以及图中所画的特定的焊缝微观相区范围。铁素体生成元素包括在铬当量中，而奥氏体生成元素包括在镍当量中。图3-2示出了原始的Schaeffler相组分图中的一张图。这些图是预测焊缝组织研究中的一个重大进步并导致其他相组分图的开发。

Schaeffler在前人研究和自己经验的基础上提出了计算当量关系式时的各个乘积项的系数。他在自己研究的基础上，假设Si、Mo和Ni的系数分别为2.5、1.8和2，并指出这和Thielemann、Compbell和Thomas建议的数据相符。原始的Schaeffler镍当量公式^[19]是：

Ni_eq=Ni+0.5Mn+30C^[1] （3-7）

当把Newell-Fleischman关系式[式（3-1）]重组，分开正数项和负数项后，则在等号的一侧就是镍当量关系式，这和Schaeffler的关系式相同而在等号的另一侧是铬当量关系式。Schaeffler对这个式子进行了修正。原始的Schaeffler铬当量关系式^[19]为：

Cr_eq=Cr+2.5Si+1.8Mo+2Nb （3-8）

值得指出：尽管氮表现为一个很强的奥氏体形成元素，但是Schaeffler在镍当量关系式[式（3-7）]中没有包括氮的项。这可能是由于在当时氮的含量很难测定的缘故。

表3-1 铬当量和镍当量表达式中各种合金元素的系数

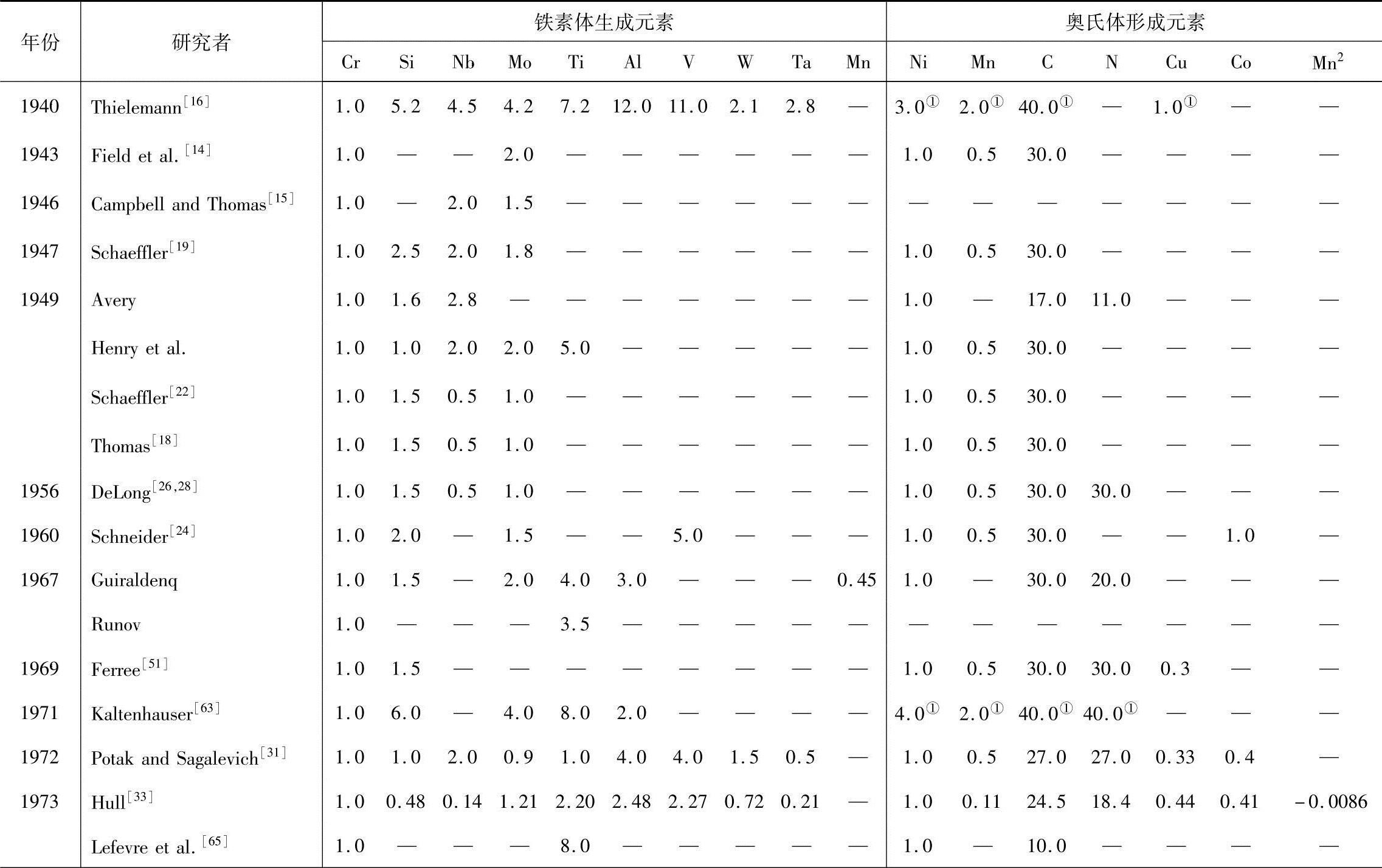
（续）

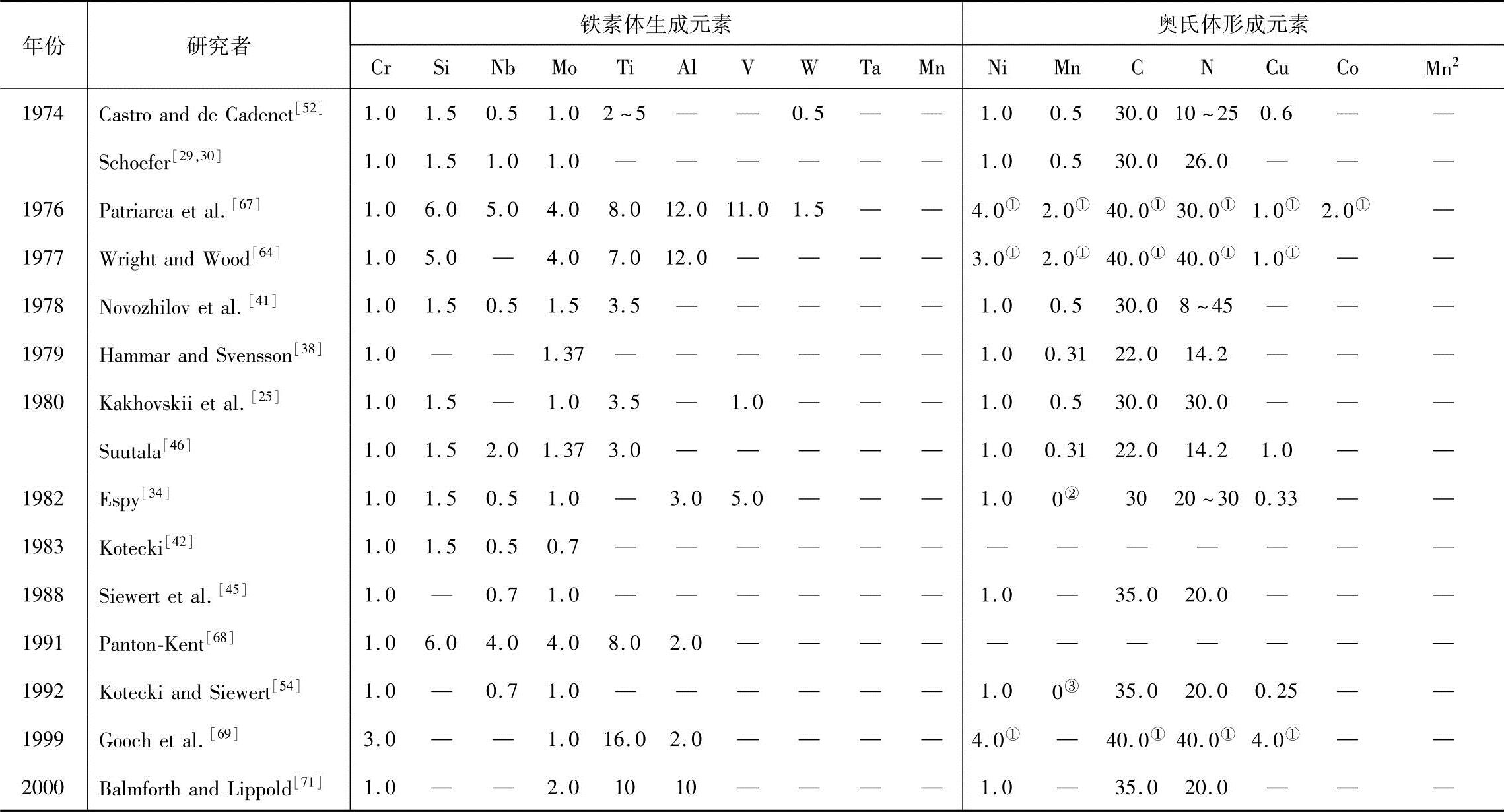
①这些系数不是镍当量系数，而是除以Ni的系数后才是镍当量系数。

②这个锰系数要换成一个常数项0.87。

③这个锰系数要换成一个常数项0.35。

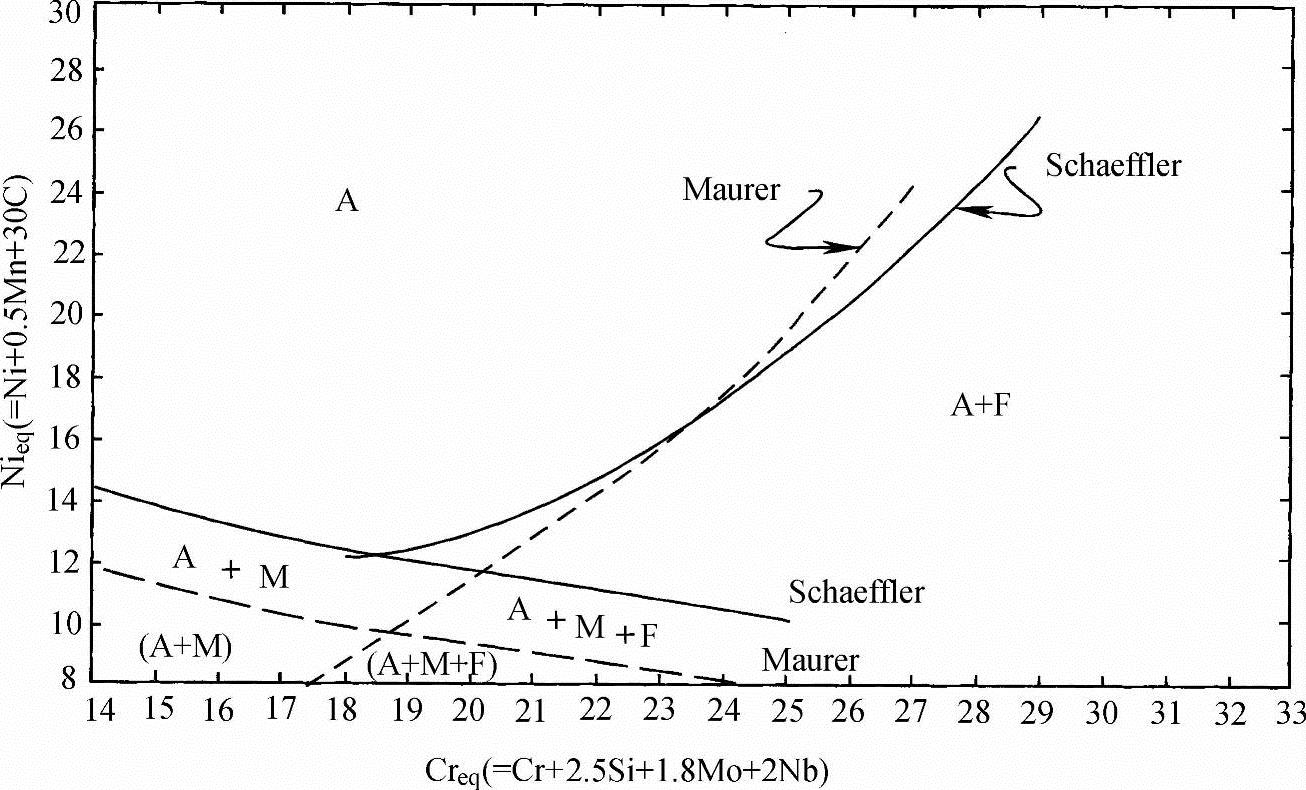
图3-2 1947年的Schaeffler相组分图，为了比较也画出了Srauss-Maurer的相组分图中的曲线

（引自Schaeffler¹⁹，美国焊接学会授权）

图3-2所示的相组分图是由焊条电弧焊（SMAW）过程来开发的，焊条电弧焊焊缝中的氮的质量分数可估计为0.06%左右。因为氮含量很低，所以Schaef_- fler没有考虑其为合金元素，只是把氮的质量分数0.06%作为不变值设定在相组分图中。这张相组分图对于当时使用常规焊条电弧焊的大多数300系列的不锈钢是相当精确的。

Schaeffler对于全奥氏体钢和含有奥氏体和铁素体的钢之间的相界线也提出了一个新的方程。这个界定奥氏体稳定性的等式是^[19]：

式中 Ni_eq———镍当量；(www.xing528.com)

Cr_eq———铬当量。

这个方程与Newell-Fleischman和Field等的等式[式（3-3）]的不同点是最后那个常数项。值得指出的是这个等式隐含一条有曲率的曲线，而图3-2原始的Shaeffler图中的线条就是弯曲的。而直到1969年当Griffith和Wright^[20]用下式界定奥氏体和奥氏体+铁素体相区界线时才揭示了标志奥氏体稳定性的二次曲线性质。

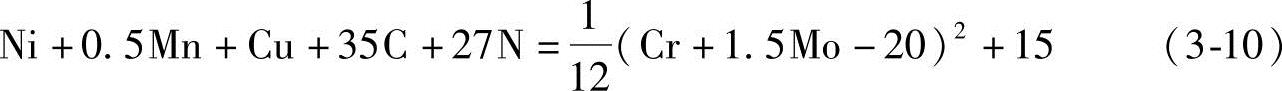
Schaeffler在1948年又进一步修改了他提出的相组分图^[21]如图3-3。请注意图中奥氏体和奥氏体+铁素体的界线成了直线。

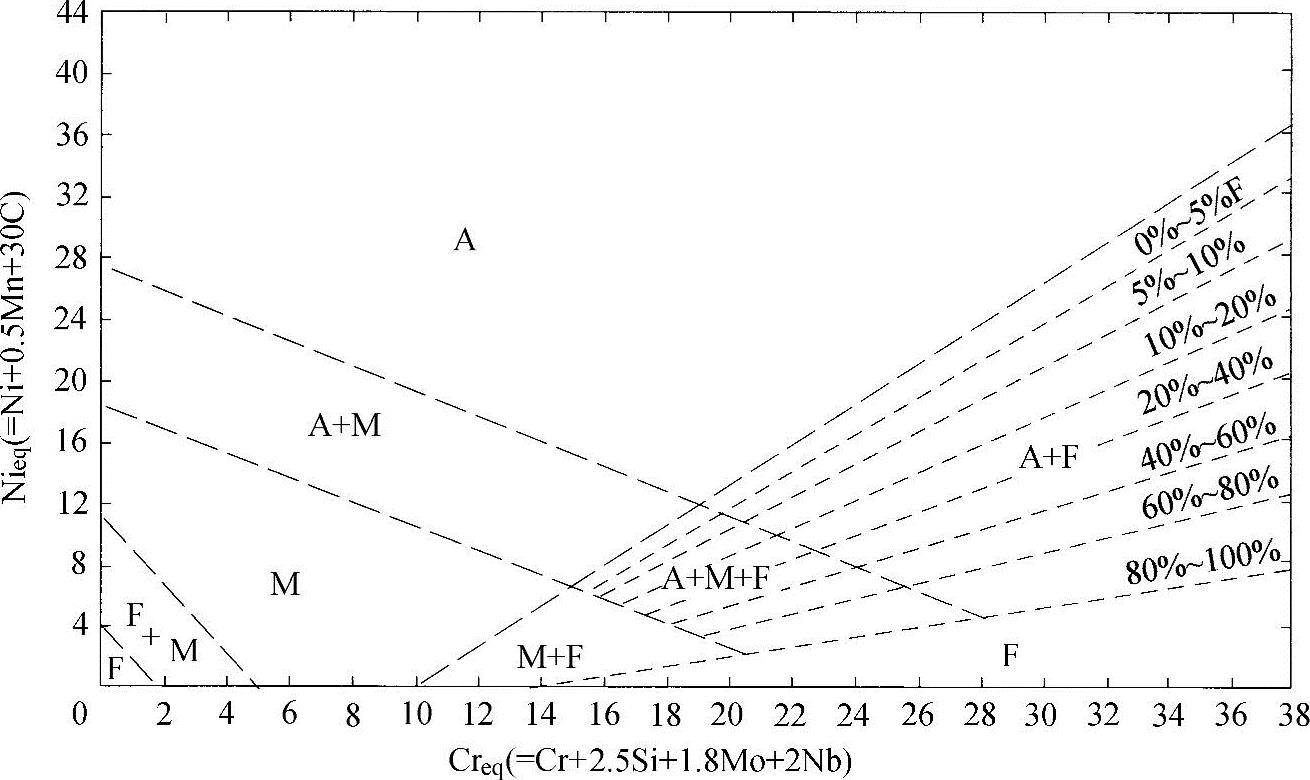
图3-3 1948年的Schaeffler相组分图，其中画有直线型的相区界线

（引自Schaeffler^[21]）

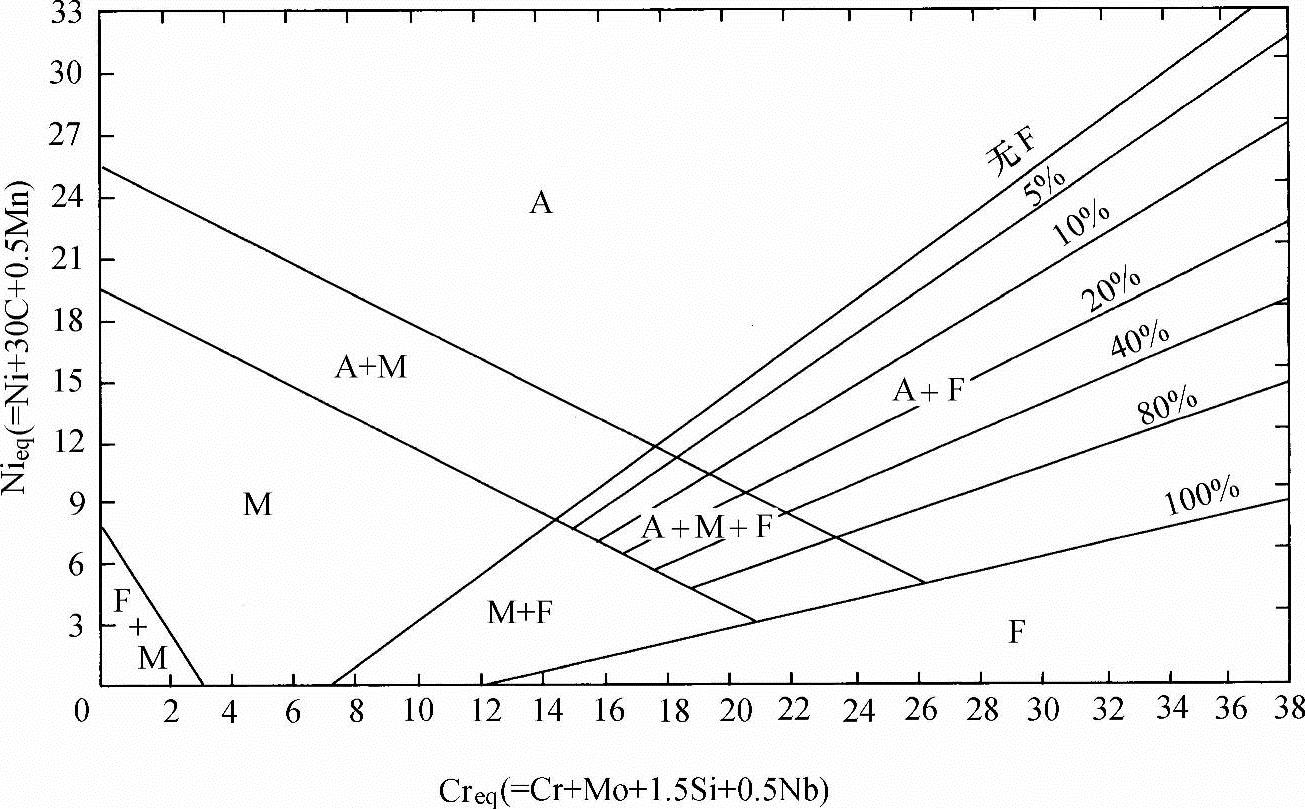
图3-4 至今仍在使用的1949年的Schaeffler相组分图

（引自Schaeffler^[22]，美国金属学会国际授权）

这张图在奥氏体+铁素体的两相区添加了等铁素体线而保留了原来的当量式。这就使得定量预测焊缝金属组织的能力增强了。1949年Schaeffler发表了他最后一版的相成分图^[22]，如图3-4所示，这张图至今尚在使用。这一版是对焊缝金属进行了很多附加的检测后得到的结果，其中修正了硅、钼和铌的系数并微调了相区界线的位置。新的铬当量式改变为

Cr_eq=Cr+Mo+1.5Si+0.5Nb （3-11）

用Shaeffler的当量关系式（Cr_eq和Ni_eq），Seferian^[23]提出了一个计算在奥氏体焊缝金属中δ铁素体含量的表达式

δ铁素体=3（Cr_eq-0.93Ni_eq-6.7） （3-12）

其他研究人员也提出了和Schaeffler相组分图类似的相组分图。1960年Schneider^[24]开发了一种相组分图来预测铸件的微观组织，如图3-5所示。这张相组分图在镍当量关系式中加了Co，在铬当量关系式中加了钒而去掉了铌。

Kakhovskii等^[25]提出了如图3-6所示的修正后的Schaeffler相组分图，其中把氮的作用量化后放入镍当量关系式，并在铬当量关系式中加入了钛和钒。

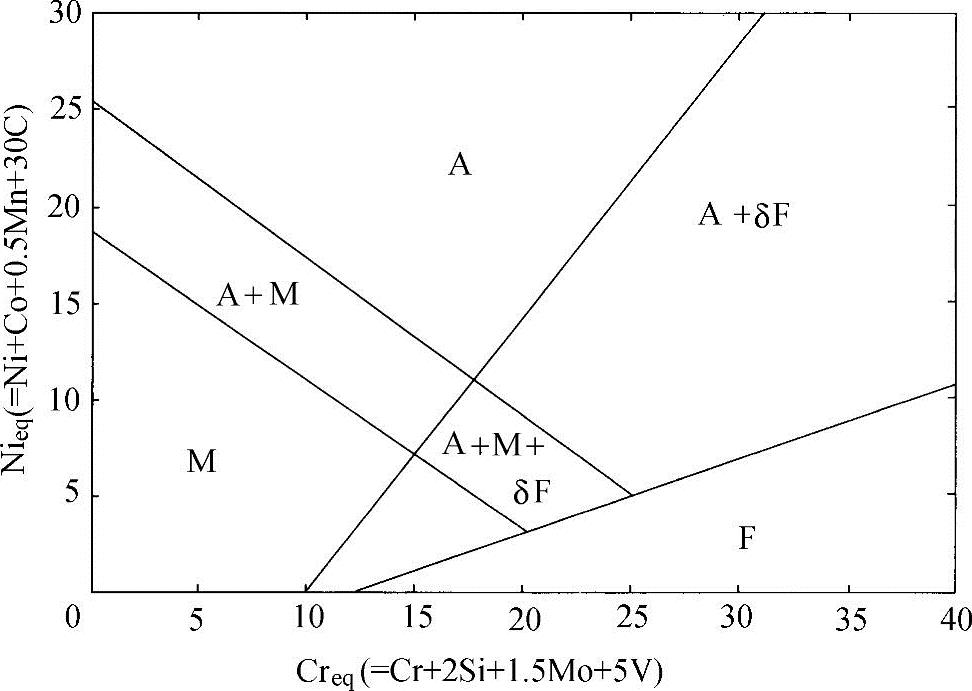
图3-5 用于铸造材料的Schneider相组分图

（引自Schneider^[24]）