至今在预测不锈钢焊缝相组分方面最感兴趣的还是奥氏体和奥氏体-铁素体合金系。这种兴趣开始于1920年，当年Strauss和Maurer[10]介绍了一张镍-铬二元素相组分图，这张图可用来预测锻压后缓慢冷却的钢微观组织中的相组分。这个相组分图中只含有奥氏体、马氏体、托氏体（过去表示回火马氏体和贝氏体组织的名称）和珠光体各相的稳定界线。以镍和铬的含量分别作为y轴和x轴，这张相组分图显示这两个元素以及它们的相互作用对锻压合金显微组织的影响。这张图的设计成为随后很多相组分图仿效的榜样。
在1939年Scherer等修改了Strauss-Maurer相图[11]，增加了一组奥氏体-铁素体之间的相稳定界线。图3-1示出了修改的相组分图，图中使用了Strauss-Maurer图中代表实际铬和镍含量的坐标轴。图的左侧部分（此处曲线向下凹，凹面指向右上角）画着Strauss-Maurar提出的几根相稳定界线；而图的右侧部分是Scherer等提出的。使用弯曲的线条是很有意义的，在随后的30年里成为研究者采用的曲线形状。这张相组分图的成分范围（质量分数）是0～28%镍和0～26%铬，在常规的不锈钢板和焊缝的碳、硅和锰含量范围内，这张相组分图可以用来预测各个相区是否存在，作者在图中表述的相区包括奥氏体、铁素体、马氏体、珠光体和托氏体相区和这些相的混合区。虽然这张图是为锻压件开发的，但其表述的奥氏体-铁素体关系对于焊缝也还算精确，这是因为图上的尺度相对粗糙，加工过程中冷却速度的影响因为图本身的不够精确而不明显了[12]。
Newell和Fleischman[13]推导了用合金成分来表达前面图中奥氏体稳定性的关系式。他们认识到铬、镍以外的其他元素对微观组织也有影响。他们推导这个式子是为了预测是否某种铬-镍合金可用于无缝钢管的制造，结论是为了在钢坯上成功穿孔，合金中必须不形成铁素体。Newell-Fleischman界定奥氏体相区和奥氏体+铁素体相区边界线的关系式是：
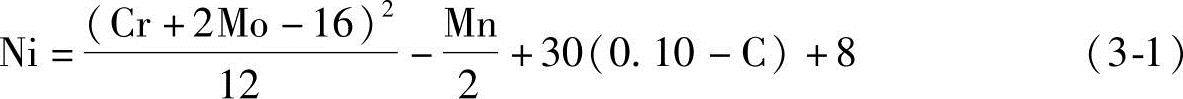
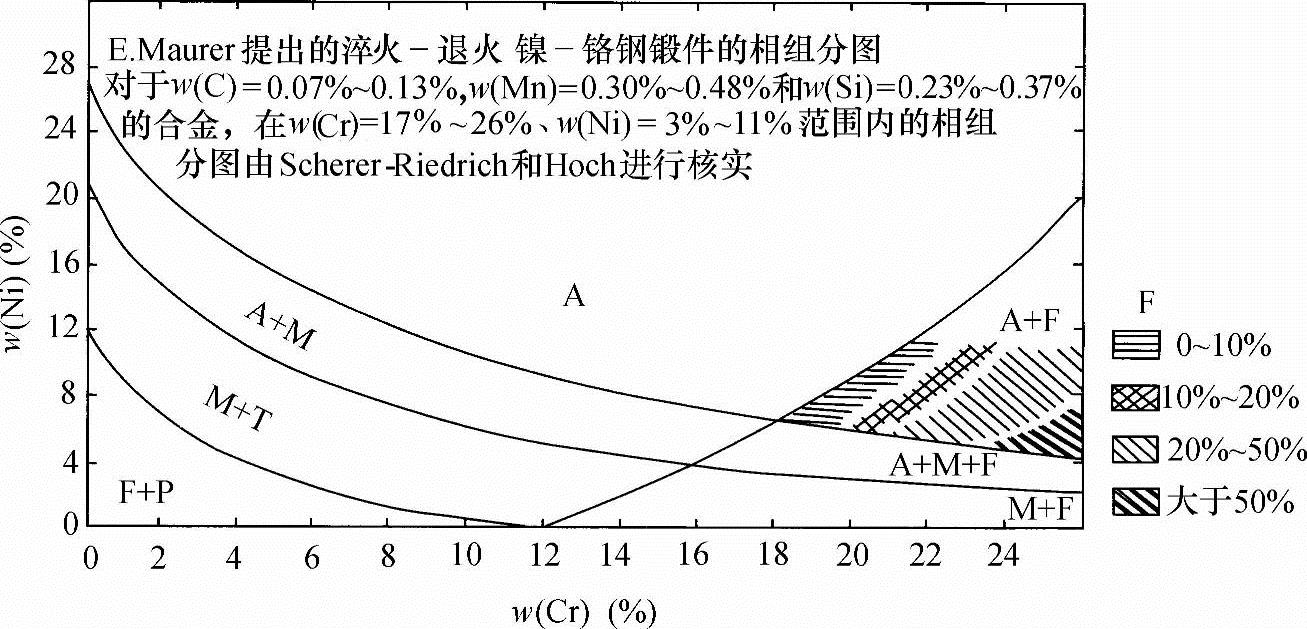
图3-1 由Scherer等修改的Strauss-Maurer镍-铬微观组织相组分图
（引自Scherer等[11]）
在式（3-1）中以及后面的公式中化学符号指的是该元素的质量分数。按式（3-1），钼生成铁素体的效应是铬的两倍；锰生成奥氏体的效应只是镍的一半，而碳是镍的30倍。在开发相组分图和预测焊缝金属微观组织方面，很多工作都集中在确定这种关系式中的系数上，这些公式被称为铬当量关系式和镍当量关系式。
在二战期间用不锈钢焊条焊接装甲成为很关注的课题。1943年Field等[14]在研究装甲焊接时确认Newell-Fleischman公式不能直接用于焊缝熔敷金属。为了使公式适用于比锻压件冷却速度快得多的焊缝金属，式（3-1）中的常数项8要改为11。这是考虑到在主要是奥氏体的焊态微观组织中某些铁素体可能在更高的镍含量下形成。这样界定奥氏体相区和奥氏体+铁素体相区边界的式子就改写为
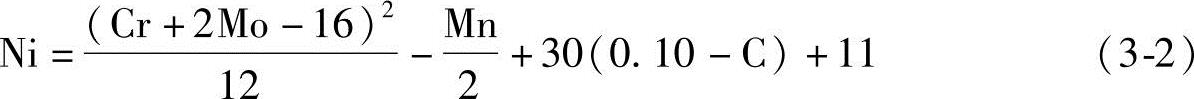(www.xing528.com)
后来式（3-2）又被改写成下面的形式，把在等号右面的铁素体形成元素和在等号左面的奥氏体形成元素分开。
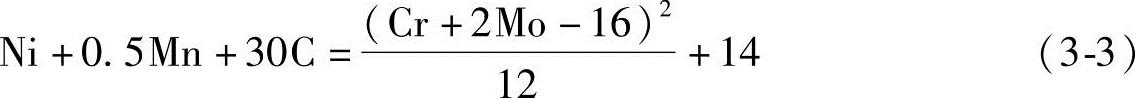
另外一些研究者也开始认识到各种元素可以组合到当量关系式中。Campbell和Thomas[15]在他们对25Cr-20Ni焊缝金属的研究中指出铬、钼和铌的组合如何影响钢的微观组织和性能，他们为这种组合中的相关关系提出了一个铬当量关系式：
铬当量=Cr+1.5Mo+2Nb （3-4）
在平衡相图的基础上Thielelmann[16]指出了各种合金元素对扩张奥氏体回线的作用，并和铬进行比较。他认为把各种合金元素的相对效应表达成铬的相当效应是比较方便的，因为铬实际上存在于所有可用于高温的合金中，而且铬是在铁基合金中所有能减少奥氏体相（即促使生成铁素体）的常用元素中效应最弱的一个元素。表3-1示出了Thielelmann提出的各种元素的铬当量系数。Binder等[17]在研究各种元素对低碳奥氏体铬-镍钢的晶间腐蚀影响时提出下列界定相对于δ铁素体相的奥氏体相稳定性边界的等式：
30C+26N+Ni-1.3Cr+11.1=0 （3-5）
Thomas[18]提出了一个线性方程用来预测相对于δ铁素体相的奥氏体相的稳定性，其中包括了添加元素的项：
Ni+0.5Mn+30C=1.1（Cr+Mo+1.5Si+0.5Nb）-8.2 （3-6）
这些线性方程成为当今使用的线性相组分图的先驱。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
