焊接构件疲劳试验探究

在实际载荷条件下进行整体焊接结构的疲劳试验是困难的。在许多情况下，可根据焊接细节的特点，通过小尺寸试样的试验结果来评价整体焊接结构的疲劳性能。这样做的前提是通过试样试验获得的疲劳特性可如实反映实际结构在材料类型、断面厚度、表面状况、接头类型、残余应力和疲劳载荷等方面的特点。因此实验室试件的焊接应与实际结构的焊接一致，而试件试验载荷与实际结构服役中所承受的载荷也应一致。

3.4.5.1 疲劳试样

1.试样的设计

试样的设计应依据试验的目的，同时考虑诸如可用的疲劳试验设备、材料和时间等实际条件的限制。如果试样用来模拟实际结构的焊接接头，则试样应在材料、焊接细节、几何形状、尺寸和制造质量等方面与实际结构尽可能相似。另外，试样设计中还应考虑加载方式，以保证试验中试件所承受的载荷与实际结构单元的一致性。

如果要获得S-N曲线，则应通过多组标称试样试验，这些试样可从适当的焊接板中切取，如图3.4-23所示。垂直板条横向焊接在基板的整个宽度上，然后切割试样，并将边缘打磨光滑。类似地，可从管的对接接头或角接接头的周向切取条状试样。然而，这些方法仅适用于焊接细节为连续焊缝且与疲劳载荷方向垂直的情况。其他情况下，每一试样都需要单独加工，如图3.4-24所示。

由于焊接和后续加工，焊接结构中常存在残余应力。大多数情况下，残余应力值可以达到屈服强度甚至抗拉强度。疲劳过程中残余应力的影响相当于提高了拉伸平均应力。多数疲劳设计准则均提供包含拉伸残余应力影响的设计数据。但应指出，小尺寸焊接试样中很难包含高的焊接残余应力，为此，可在钢试样中通过点加热来引入残余应力，或者通过载荷的合理选取来模拟残余应力的影响。

需要注意的是应保证试样的疲劳失效发生在所关注的焊缝细节而不是过早地发生在与试验方法有关的其他位置。在这方面，如果运用楔形夹具装夹轴向载荷试样，由于夹具处的缺口效应，破坏一般发生在装夹部位。这一问题对于具有高疲劳强度的焊缝来说尤其严重。可采用变断面试样来避免这一问题，变断面试样中载荷最大部位的尺寸比试样装夹部位小。类似地，对弯曲疲劳试验，由于装卡处的缺口效应或试样中局部剪切应力过高，破坏常发生在加载点。图3.4-25给出了疲劳试验试样的一般建议尺寸。

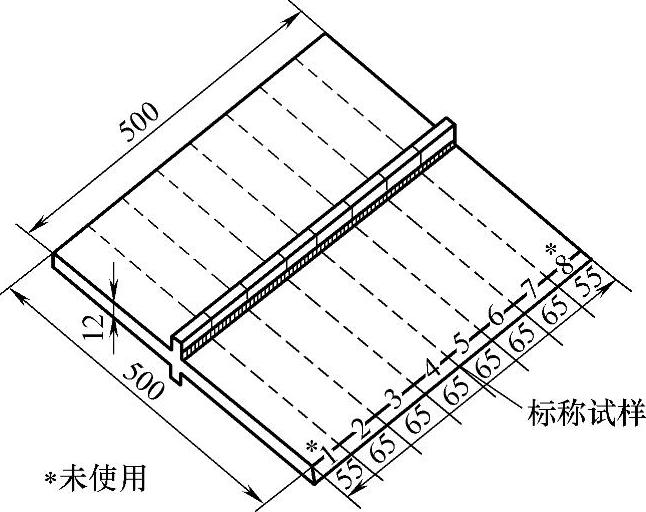
图3.4-23 疲劳试样切取示例

图3.4-24 需要单独制作的疲劳试验试样示例

2.试样的制备

疲劳试样的材料应与实际焊接构件或结构相同，即应具有相同的规格和厚度。但在实际上，由于一些焊接接头的疲劳性能与材料的拉伸强度关系不大，允许在材料等级和厚度的选择上根据具体情况灵活处理。

疲劳试样的焊接应按照实际结构或构件焊接中经过评定的焊接工艺规范进行。图3.4-23所示的用于加工小尺寸疲劳试样的焊接试板应具有与实际结构相同的焊接热过程及焊缝布置，即保证轧制方向应与原始结构相同。有时为模拟实际条件，试板中还应包含起弧与熄弧点。

如果试验用来验证一个特定的焊接构件或结构，则这一结构或构件中每一焊接接头类型的尺寸和相应参数都应表征。在电弧焊中，这些参数包括：板厚、母材类型、轧制方向、焊接方法、保护气体类型、焊接位置（平焊、仰焊等）、焊接速度、预热温度、焊后热处理、焊接过程中的电参数、焊缝的尺寸与形状、电极类型与直径、焊道顺序以及起弧与熄弧位置等。

图3.4-25 焊接接头拉伸和弯曲疲劳试样

a）轴向加载 b）三点弯曲 c）四点弯曲

还应注意，试板焊接后的其他处理如焊缝清理、喷丸或涂覆等应与实际焊接结构或构件相同。

对接接头和十字接头中常常存在错边，其主要原因是焊接过程中的变形、焊件断面尺寸或厚度的变化以及焊接组装的困难等。被焊部件的不对中或角变形会引起轴向加载时载荷的偏心，如图3.4-26所示。这种载荷的偏心会引起附加弯矩，进而影响疲劳性能。

从焊接板中或焊接管中切取小试样时，尽可能采用锯切或机械加工的方法。如果要采用火焰切割的方法，则应注意避免试样的变形，并将火焰切割的边缘加工或打磨光滑。为避免疲劳裂纹在试样边缘处萌生，应保证试样边缘纵向光滑。

有时，对弯曲的焊接试样需要矫直，这可以通过局部弯曲来完成。但在这一过程中，应避免试验焊缝附近（特别是焊趾处）产生二次弯曲。二次弯曲往往产生残余应力，对焊接试样的疲劳性能的测试结果有明显影响。

如果有可能测量偏心，则可计算以膜应力分量σ_m表征的二次弯曲应力σ_s，计算公式列于表3.4-7。图3-4-27给出了测量中心线错边e和接头变形角α所引起的轴向偏心的示意图。测量可采用千分表或其他相应工具进行。

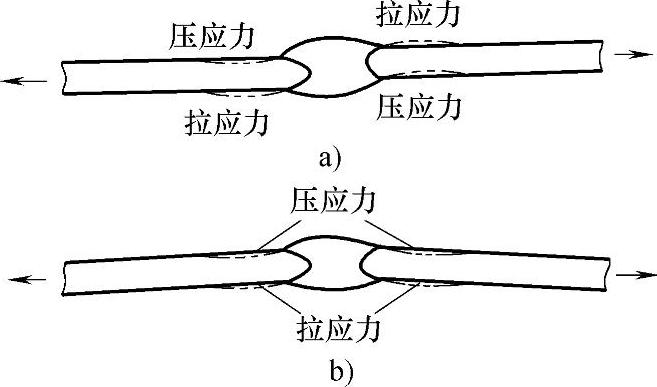
图3.4-26引起焊接接头附加弯曲应力的变形

a）轴向错边b）角变形

图3.4-27采用千分表测量偏心的示意图

角变形

轴向偏心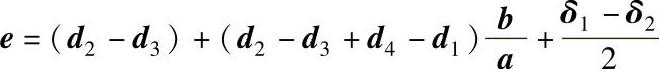

应该指出的是，除非使用非线性双曲正切修正Δσ_s/Δσ_m=σ_s/σ_m，否则试验中σ_s应取施加应力的最大值和最小值来计算Δσ_s。修正后的最终应力幅为Δσ_cor=Δσm+Δσ_s。

也可通过对焊接接头附近实际应力的测定来进行修正，如电阻应变片法。此时，修正的应力幅Δσ_cor由下式给出

式中 Δσ_m——所施加的名义轴向应力或膜应力；

Δε_F和Δε_B——试样两表面测得的应变。

在实际中，有时还要确定焊缝局部的几何尺寸。焊缝局部几何尺寸通常由两个参数来表征，即焊缝表面与被焊板面间的过渡角（θ）和半径（ρ），如图3.4-28所示。

图3.4-28 焊缝局部几何示意图

焊接残余应力的性质与分布对疲劳性能有较大影响。循环载荷的施加或疲劳裂纹的扩展将会使原始残余应力重新分布。因而残余应力的测量（特别是疲劳裂纹萌生处）应在疲劳试验前进行。焊接残余应力的测量可采用截条法、盲孔法或X射线衍射法。X射线衍射法可测量焊趾局部（小于1mm宽）的残余应力及应力梯度，如图3.4-29所示。

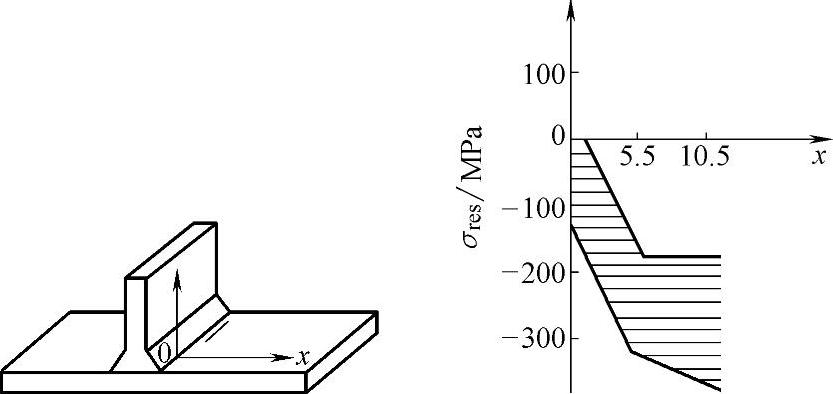
图3.4-29 焊趾局部残余应力及X射线衍射峰的宽度

3.4.5.2 疲劳试验

1.名义应力（或应变）幅的确定

目前有关焊接接头疲劳设计的S-N曲线大多给出了以疲劳裂纹萌生处的名义应力幅表征的疲劳强度。焊接构件的疲劳试验也应遵循这一原则，其疲劳强度也用名义应力幅来表征。图3.4-30给出了拉伸或弯曲载荷下，带有横向角焊缝加强筋的平板试样焊趾处失效时名义应力幅Δσ_nom的定义。

对于严重变形和偏心的情况，计算Δσ_nom时应考虑附加二次弯曲应力。

2.结构热点应力（或应变）幅的确定

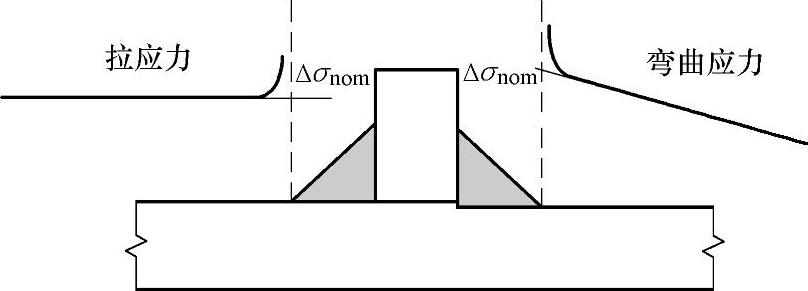
图3.4-30 角焊缝试板拉伸或弯曲时名义应力的定义(www.xing528.com)

表3.4-7 十字接头或对接接头偏心引起的二次弯曲应力的计算公式

对于焊趾破坏为主的疲劳情况，常采用热点应力幅Δσ_shs来表征。焊趾处的结构热点应力幅包含了接头几何应力集中和二次应力的影响，但不包括焊趾处局部缺口的效应。结构热点应力幅可通过测量焊趾附近表面的应力分布来确定，如图3.4-31所示。对复杂结构，结构热点应力也可通过有限元分析来确定。对管状接头，可采用一些参数化公式来计算结构热点应力集中系数。

图3.4-31 线性外推法确定焊趾表面的结构热点应力幅

3.保守载荷条件

疲劳试验中试样的尺寸与实际结构或构件相比都比较小，为能在小尺寸试样的试验中考虑实际结构中存在的较高的焊接残余拉伸应力，常在试验中提高应力比（通常R﹥0.5）或提高拉伸平均应力或峰值拉伸应力，这样测得的疲劳性能数据均比较保守。最严苛的条件是在最大应力为拉伸屈服应力下的循环试验，这将会产生最为保守的结果。在这种高拉伸循环应力条件下得到的S-N曲线通常比一般条件下的S-N曲线要低并且陡。这一曲线可作为类似接头中任何疲劳载荷下的S-N曲线的极限情况。

需要指出的是，由于焊接残余应力的分布及演变，上述处理方法在某些场合下过于保守。例如，在锤击焊道或焊趾的情况下，焊趾处局部残余应力会得到松弛，疲劳性能会得到改善。在变幅加载条件下，局部残余应力也会因所施加的循环载荷而演变，上述处理方法给出的结果会过于保守。

4.疲劳寿命的确定

在开始疲劳试验之前，应确定疲劳失效判据，并在进行的系列疲劳试验中采用所选定的同一失效判据。典型的失效判据可以是：试样的完全断裂、达到规定的疲劳裂纹长度（如可检测到的宏观裂纹、裂纹的具体尺寸、裂纹贯穿板厚等）、达到试验设备或加载条件的极限（如过大偏差、载荷或试验设备不稳定等）、一定的循环数。

需要指出的是，焊接接头疲劳设计S-N曲线中用到的失效判据是裂纹穿透壁厚，以及达到所规定的疲劳极限（如10⁷次循环）。

在疲劳试验中，可采用多种方法检测疲劳裂纹的萌生并据此确定疲劳裂纹出现时的循环数。这些方法包括：焊趾处应变计测量方法、电压降法、柔度法、超声法、放大镜观察法、微裂纹复膜法等。

3.4.5.3 疲劳极限

按照已有的疲劳试验方法（例如ASTME466或E468）来测定Δσ-N（S-N）曲线、给定循环下的疲劳强度或疲劳极限。

通常情况下，一般测定在2×10⁶或10⁷次循环周期下的疲劳强度作为特征疲劳强度（Δσ_N或S_N）的参考值。

可采用多种统计学方法评价所测得的S-N曲线的疲劳强度及其标准差。

可采用类似于表3.4-8所示的升降法来测试给定循环的疲劳强度。这一方法需要对试样施加根据前次试验结果确定的应力幅。如果前次试样“i”在S_i水平发生失效，下一个应力水平将会是S_i+1=S_i-d，其中d是预先确定的所施加应力水平的增量（理论上在S和2S之间）。如果前次试验中试样没有破坏，则S_i+1=S_i+d。

表3.4-8 升降法试验

（续）

一般情况下，11～15件试样足以测定所需的疲劳强度，可利用在每一应力水平f_i下获得的越出试件数以及表3.4-8所定义的参数F、A和B来估算（其中i=0对应最低的应力水平）。这样，在给定的循环数下疲劳强度的平均值S_N为：

S_N=S₀+d（A/F±0.5）

式中 S₀——小概率事件（试件越出或失效）出现时对应的最低应力水平（i=0）。

当小概率事件为越出时采用数值+0.5，当小概率事件为失效时用-0.5。S_N的标准偏差的估计值由下式给出：

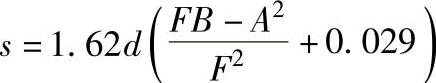
作为例子，表3.4-8给出了试验结果S_N和s的估计值。

针对不同需要，S-N曲线一般是在一定的循环数范围内建立的，大多关注有限寿命区间。在双对数坐标系中，有限寿命部分的S-N曲线呈线性。这种情况下，疲劳试验主要在2×10⁶循环以内进行，以避免试验结果处于疲劳极限的过渡区（即10⁵到2×10⁶循环区间）。如果要确定全S-N曲线，循环寿命区间应延伸至疲劳极限所在的范围（10⁴<N<10⁷循环）。考虑到疲劳性能的统计学变化，可在3或4个不同的Δσ水平上进行疲劳试验。理论上，建立S-N曲线应进行尽可能多的试样的试验，但由于时间、材料和经费等的限制，实际试验中的试样数是有限的。一般情况下，建议进行8～10组试验。

特别地，若确信所关注的寿命区间，S-N双对数坐标系中存在线性关系，两个应力水平即可完成试验。

3.4.5.4 疲劳试验的统计学分析

多种统计学方法可用于分析疲劳试验结果、确定统计参数以及绘制失效概率的Δσ-N曲线。表3.4-9给出了国际焊接学会所建议的主要统计分析方法。

表3.4-9 疲劳试验结果统计学分析方法

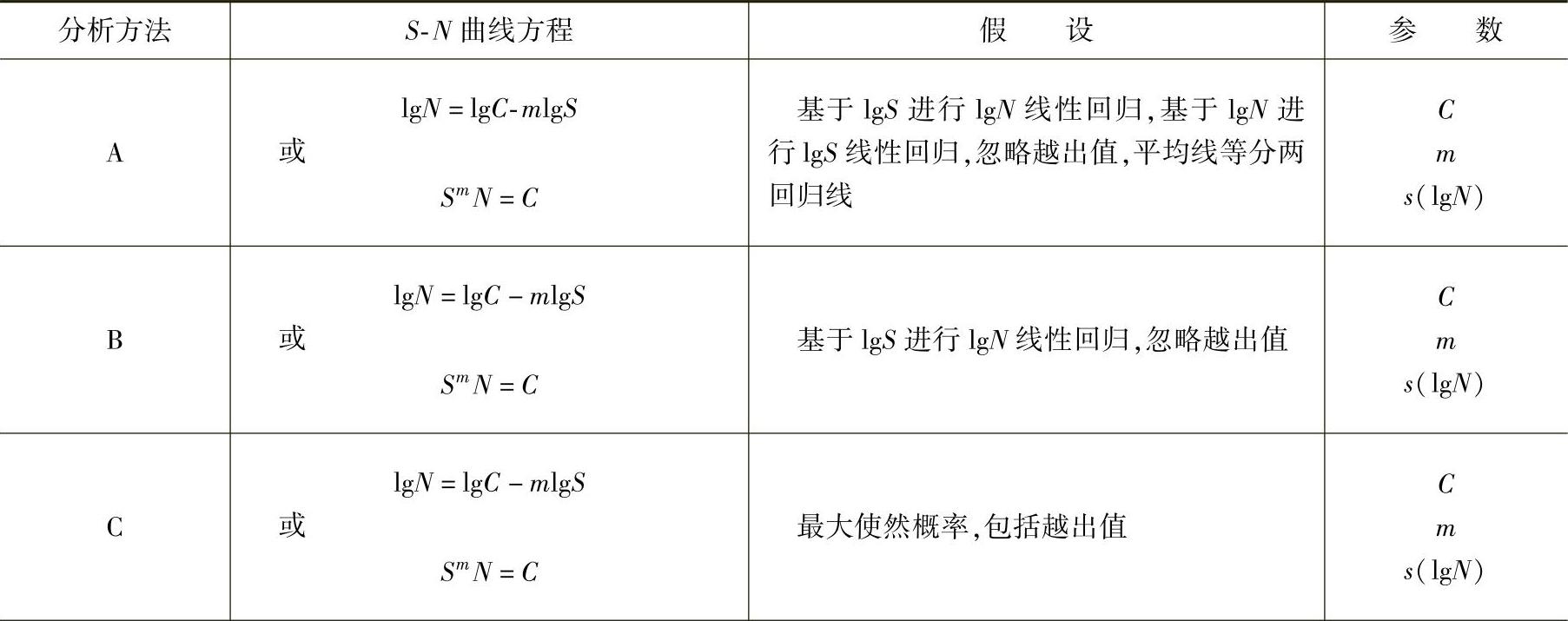
（续）

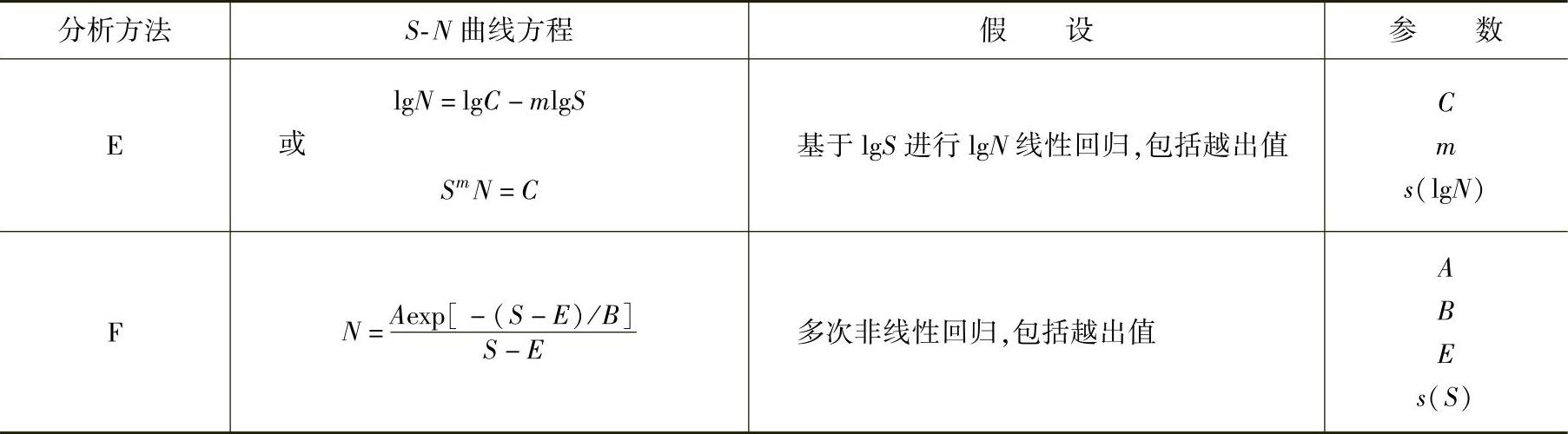
1.方法A

运用最小二乘法通过回归分析获得线性lgS-lgN曲线，忽略越出值。分析时假定lgN为因变量，lgS也是因变量。最终的S-N曲线由一条将两回归线平分的直线获得。

2.方法B

运用最小二乘法通过回归分析获得线性lgS-lgN曲线，忽略越出值。分析时假定lgN为因变量，lgN的标准偏差s（lgN）用来定义置信区间。

方法A和B没有考虑非破坏试样（越出）。下面的三种方法分析中考虑了溢出。

3.方法C

用最大似然法和lgS的标准偏差s（lgS）来建立S-N曲线和置信区间。

4.方法D和E

通过计算机程序，采用Bastenaire方法可拟合任何形式的S-N曲线。可以考虑两种模型。

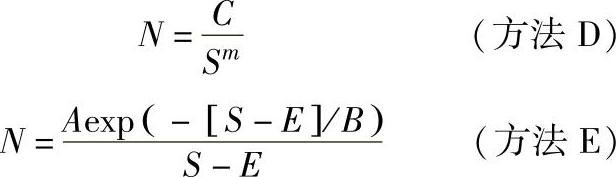
式中 A、B和E——统计得出的参数。

应该注意的是，公式S^mN=C给出的结果比较离散。对于给定的疲劳寿命，S值之间的偏差相对较小。将S-N曲线外推到可用试验数据范围以外是危险的。方法A和B中的统计学方法不适用于不同来源的疲劳数据。对不同来源试样的疲劳性能评价需要采用不同的方法，这要求基于大量试样组的试验研究。